Question Number 180400 by a.lgnaoui last updated on 12/Nov/22
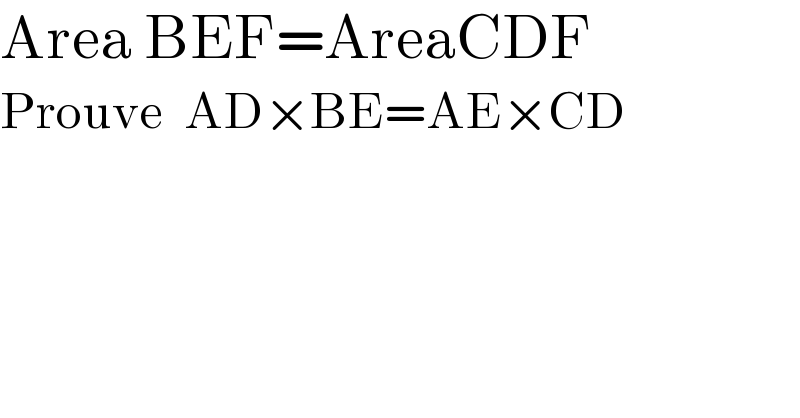
$$\mathrm{Area}\:\mathrm{BEF}=\mathrm{AreaCDF} \\ $$$$\mathrm{Prouve}\:\:\mathrm{AD}×\mathrm{BE}=\mathrm{AE}×\mathrm{CD} \\ $$
Commented by a.lgnaoui last updated on 12/Nov/22
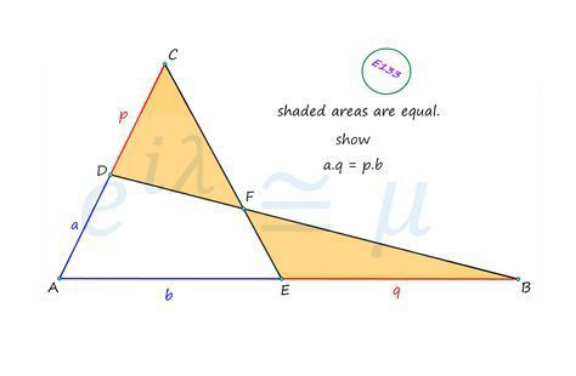
Answered by Acem last updated on 12/Nov/22
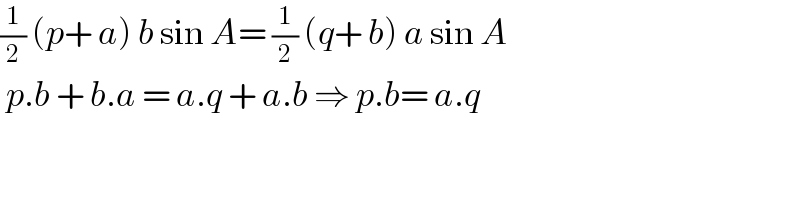
$$\frac{\mathrm{1}}{\mathrm{2}}\:\left({p}+\:{a}\right)\:{b}\:\mathrm{sin}\:{A}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left({q}+\:{b}\right)\:{a}\:\mathrm{sin}\:{A} \\ $$$$\:{p}.{b}\:+\:{b}.{a}\:=\:{a}.{q}\:+\:{a}.{b}\:\Rightarrow\:{p}.{b}=\:{a}.{q} \\ $$$$ \\ $$
Answered by HeferH last updated on 16/Nov/22

$$\:\mathrm{1}.\:{Area}\:{DCB}\:=\:{Area}\:{EBC} \\ $$$$\:{but}\:{DCB}\:{and}\:{EBC}\:{have}\:{the}\:{same}\:{base},\:{so} \\ $$$$\:{they}\:{need}\:{to}\:{have}\:{the}\:{same}\:{height} \\ $$$$\:\left({since}\:{their}\:{areas}\:{are}\:{equal}\right)\:\Rightarrow\:{DEBC}\:{is} \\ $$$$\:{a}\:{trapezoid}\:\Rightarrow\:{DE}\:\mid\mid\:{CB} \\ $$$$\:\mathrm{2}.\:{By}\:{using}\:{similar}\:{triangles} \\ $$$$\:\frac{{AD}}{{AD}\:+\:{DC}}\:=\:\frac{{AE}}{{AE}\:+\:{EB}} \\ $$$$\:{AD}\centerdot{AE}\:+\:{AD}\centerdot{EB}\:=\:{AD}\centerdot{AE}+\:{AE}\centerdot{DC} \\ $$$$\:{AD}\:\centerdot\:{EB}\:=\:{AE}\:\centerdot\:{DC}\:\checkmark \\ $$$$\: \\ $$
