Question Number 93855 by Ar Brandon last updated on 15/May/20

$$\mathrm{At}\:\mathrm{what}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parabola}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{will}\:\mathrm{the}\:\mathrm{tangent}\: \\ $$$$\mathrm{a}\backslash\:\mathrm{be}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{4x}−\mathrm{5} \\ $$$$\mathrm{b}\backslash\:\mathrm{be}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{2x}−\mathrm{6y}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{c}\backslash\:\mathrm{make}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{45}^{°} \:\mathrm{with}\:\mathrm{3x}−\mathrm{y}+\mathrm{1}=\mathrm{0} \\ $$
Answered by Kunal12588 last updated on 15/May/20
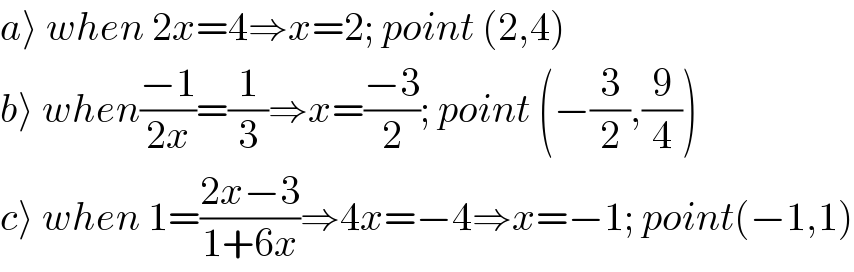
$${a}\rangle\:{when}\:\mathrm{2}{x}=\mathrm{4}\Rightarrow{x}=\mathrm{2};\:{point}\:\left(\mathrm{2},\mathrm{4}\right) \\ $$$${b}\rangle\:{when}\frac{−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{x}=\frac{−\mathrm{3}}{\mathrm{2}};\:{point}\:\left(−\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{4}}\right) \\ $$$${c}\rangle\:{when}\:\mathrm{1}=\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{1}+\mathrm{6}{x}}\Rightarrow\mathrm{4}{x}=−\mathrm{4}\Rightarrow{x}=−\mathrm{1};\:{point}\left(−\mathrm{1},\mathrm{1}\right) \\ $$
