Question Number 183202 by liuxinnan last updated on 23/Dec/22
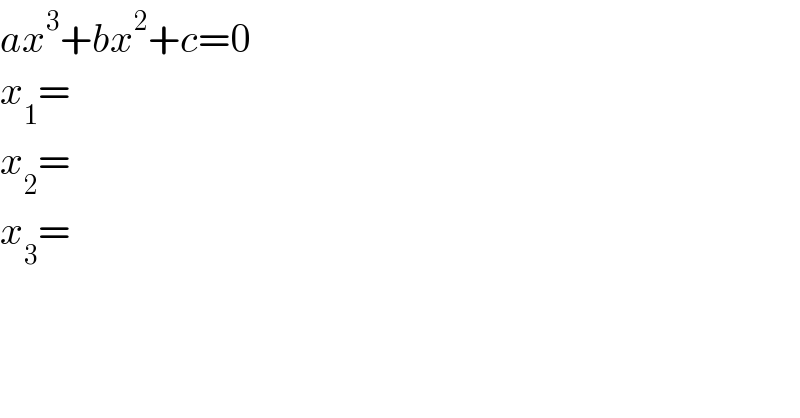
$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{c}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} = \\ $$$${x}_{\mathrm{2}} = \\ $$$${x}_{\mathrm{3}} = \\ $$
Answered by Frix last updated on 23/Dec/22
![ax^3 +bx^2 +c=0 m=(b/a)∧n=(c/a) x^3 +mx^2 +n=0 x=t−(m/3) t^3 +(m^2 /3)t+((2m^3 )/(27))+n=0 p=(m^2 /3)∧q=((2m^3 )/(27))+n t^3 +pt+q=0 Depending on D=(p^3 /(27))+(q^2 /4) =_< ^> 0 you can use Cartano′s Formula or the Trigonometric Formula: D>0 ⇒ u=((−(q/2)−(√((p^3 /(27))+(q^2 /4)))))^(1/3) ∧v=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) [you must take the real roots: ((−r))^(1/3) =−(r)^(1/3) ] t_1 =u+v t_2 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v t_3 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v D=0∧p≠0∧q≠0 ⇔ (p^3 /(27))=−(q^2 /4) ⇒ u=v=((−(q/2)))^(1/3) t_1 =2((−(q/2)))^(1/3) =((3q)/p) t_2 =t_3 =−((−(q/2)))^(1/3) =−((3q)/(2p)) D<0 ⇒ t_k =((−((4p)/3)))^(1/3) ×cos (((2πk+cos^(−1) (−(q/2)×(√(−((27)/p^3 )))))/3)) with k=1, 2, 3 You must insert backwards p=(m^2 /3)∧q=((2m^3 )/(27))+n x_k =t_k −(m/3) m=(b/a)∧n=(c/a) to get the demanded formula](https://www.tinkutara.com/question/Q183204.png)
$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{c}=\mathrm{0} \\ $$$${m}=\frac{{b}}{{a}}\wedge{n}=\frac{{c}}{{a}} \\ $$$${x}^{\mathrm{3}} +{mx}^{\mathrm{2}} +{n}=\mathrm{0} \\ $$$${x}={t}−\frac{{m}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} +\frac{{m}^{\mathrm{2}} }{\mathrm{3}}{t}+\frac{\mathrm{2}{m}^{\mathrm{3}} }{\mathrm{27}}+{n}=\mathrm{0} \\ $$$${p}=\frac{{m}^{\mathrm{2}} }{\mathrm{3}}\wedge{q}=\frac{\mathrm{2}{m}^{\mathrm{3}} }{\mathrm{27}}+{n} \\ $$$${t}^{\mathrm{3}} +{pt}+{q}=\mathrm{0} \\ $$$$\mathrm{Depending}\:\mathrm{on}\:{D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}\:\underset{<} {\overset{>} {=}}\:\mathrm{0}\:\mathrm{you}\:\mathrm{can}\:\mathrm{use} \\ $$$$\mathrm{Cartano}'\mathrm{s}\:\mathrm{Formula}\:\mathrm{or}\:\mathrm{the}\:\mathrm{Trigonometric} \\ $$$$\mathrm{Formula}: \\ $$$${D}>\mathrm{0}\:\Rightarrow \\ $$$$\:\:\:\:\:{u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}\wedge{v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{you}\:\mathrm{must}\:\mathrm{take}\:\mathrm{the}\:\mathrm{real}\:\mathrm{roots}:\:\sqrt[{\mathrm{3}}]{−{r}}=−\sqrt[{\mathrm{3}}]{{r}}\right] \\ $$$$\:\:\:\:\:{t}_{\mathrm{1}} ={u}+{v} \\ $$$$\:\:\:\:\:{t}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$$\:\:\:\:\:{t}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${D}=\mathrm{0}\wedge{p}\neq\mathrm{0}\wedge{q}\neq\mathrm{0}\:\Leftrightarrow\:\frac{{p}^{\mathrm{3}} }{\mathrm{27}}=−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow \\ $$$$\:\:\:\:\:{u}={v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:{t}_{\mathrm{1}} =\mathrm{2}\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}}=\frac{\mathrm{3}{q}}{{p}} \\ $$$$\:\:\:\:\:{t}_{\mathrm{2}} ={t}_{\mathrm{3}} =−\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}}=−\frac{\mathrm{3}{q}}{\mathrm{2}{p}} \\ $$$${D}<\mathrm{0}\:\Rightarrow \\ $$$$\:\:\:\:\:{t}_{{k}} =\sqrt[{\mathrm{3}}]{−\frac{\mathrm{4}{p}}{\mathrm{3}}}×\mathrm{cos}\:\left(\frac{\mathrm{2}\pi{k}+\mathrm{cos}^{−\mathrm{1}} \:\left(−\frac{{q}}{\mathrm{2}}×\sqrt{−\frac{\mathrm{27}}{{p}^{\mathrm{3}} }}\right)}{\mathrm{3}}\right)\:\mathrm{with}\:{k}=\mathrm{1},\:\mathrm{2},\:\mathrm{3} \\ $$$$\mathrm{You}\:\mathrm{must}\:\mathrm{insert}\:\mathrm{backwards} \\ $$$${p}=\frac{{m}^{\mathrm{2}} }{\mathrm{3}}\wedge{q}=\frac{\mathrm{2}{m}^{\mathrm{3}} }{\mathrm{27}}+{n} \\ $$$${x}_{{k}} ={t}_{{k}} −\frac{{m}}{\mathrm{3}} \\ $$$${m}=\frac{{b}}{{a}}\wedge{n}=\frac{{c}}{{a}} \\ $$$$\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{demanded}\:\mathrm{formula} \\ $$
Answered by mr W last updated on 23/Dec/22
![we can also solve for (1/x) instead of for x. (1/x^3 )+(b/(cx))+(a/c)=0 Δ=(1/4)((a/c))^2 +(1/(27))((b/c))^3 if Δ>0: (1/x_1 )=((Δ−(a/(2c))))^(1/3) −((Δ+(a/(2c))))^(1/3) (1/x_(2,3) )=−(1/2)(((Δ−(a/(2c))))^(1/3) −((Δ+(a/(2c))))^(1/3) )±(((Δ−(a/(2c))))^(1/3) +((Δ+(a/(2c))))^(1/3) )i if Δ=0: (1/x_1 )=−2((a/(2c)))^(1/3) (1/x_2 )=(1/x_3 )=((a/(2c)))^(1/3) if Δ<0: (1/x_(1,2,3) )=2(√(−(b/(3c)))) sin [(1/3)sin^(−1) (((3a)/(−2b))(√(−((3c)/b))))+((2kπ)/3)] (k=0,1,2)](https://www.tinkutara.com/question/Q183206.png)
$${we}\:{can}\:{also}\:{solve}\:{for}\:\frac{\mathrm{1}}{{x}}\:{instead}\:{of}\: \\ $$$${for}\:{x}. \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\frac{{b}}{{cx}}+\frac{{a}}{{c}}=\mathrm{0} \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{a}}{{c}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{27}}\left(\frac{{b}}{{c}}\right)^{\mathrm{3}} \\ $$$$\underline{{if}\:\Delta>\mathrm{0}:} \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{1}} }=\sqrt[{\mathrm{3}}]{\Delta−\frac{{a}}{\mathrm{2}{c}}}−\sqrt[{\mathrm{3}}]{\Delta+\frac{{a}}{\mathrm{2}{c}}} \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{2},\mathrm{3}} }=−\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\Delta−\frac{{a}}{\mathrm{2}{c}}}−\sqrt[{\mathrm{3}}]{\Delta+\frac{{a}}{\mathrm{2}{c}}}\right)\pm\left(\sqrt[{\mathrm{3}}]{\Delta−\frac{{a}}{\mathrm{2}{c}}}+\sqrt[{\mathrm{3}}]{\Delta+\frac{{a}}{\mathrm{2}{c}}}\right){i} \\ $$$$\underline{{if}\:\Delta=\mathrm{0}:} \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{1}} }=−\mathrm{2}\sqrt[{\mathrm{3}}]{\frac{{a}}{\mathrm{2}{c}}} \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{2}} }=\frac{\mathrm{1}}{{x}_{\mathrm{3}} }=\sqrt[{\mathrm{3}}]{\frac{{a}}{\mathrm{2}{c}}} \\ $$$$\underline{{if}\:\Delta<\mathrm{0}:} \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{1},\mathrm{2},\mathrm{3}} }=\mathrm{2}\sqrt{−\frac{{b}}{\mathrm{3}{c}}}\:\mathrm{sin}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}{a}}{−\mathrm{2}{b}}\sqrt{−\frac{\mathrm{3}{c}}{{b}}}\right)+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right]\:\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$
