Question Number 157664 by cortano last updated on 26/Oct/21
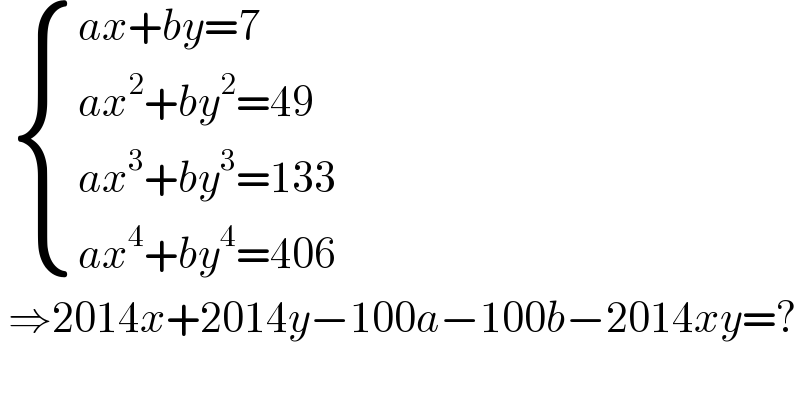
$$\:\begin{cases}{{ax}+{by}=\mathrm{7}}\\{{ax}^{\mathrm{2}} +{by}^{\mathrm{2}} =\mathrm{49}}\\{{ax}^{\mathrm{3}} +{by}^{\mathrm{3}} =\mathrm{133}}\\{{ax}^{\mathrm{4}} +{by}^{\mathrm{4}} =\mathrm{406}}\end{cases} \\ $$$$\:\Rightarrow\mathrm{2014}{x}+\mathrm{2014}{y}−\mathrm{100}{a}−\mathrm{100}{b}−\mathrm{2014}{xy}=? \\ $$
Commented by mr W last updated on 26/Oct/21
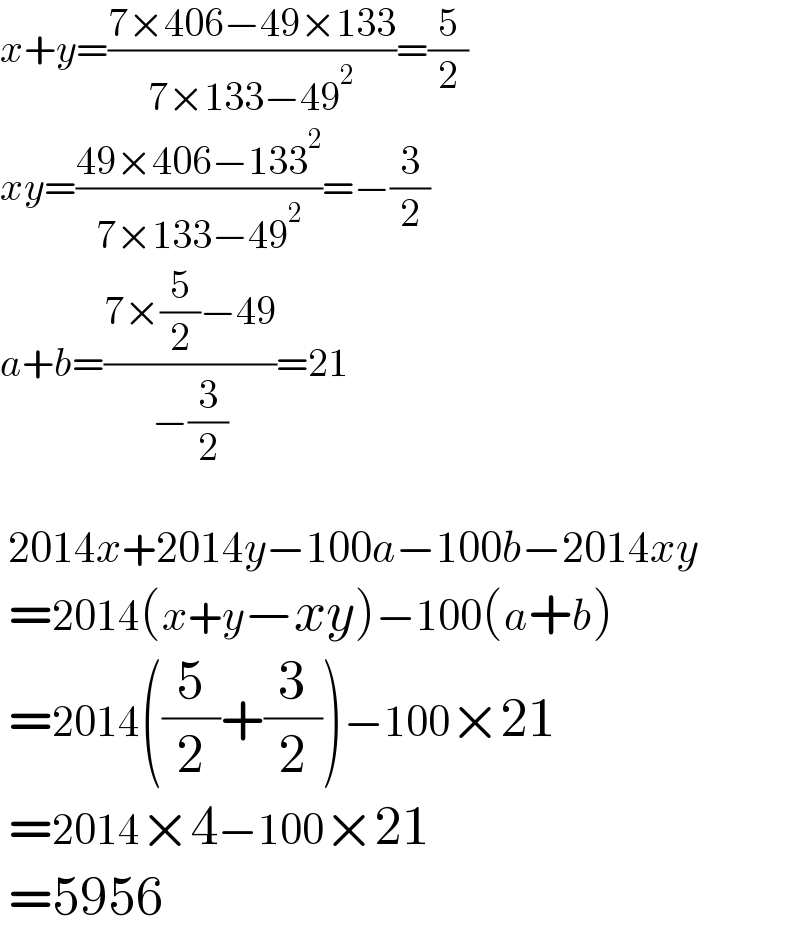
$${x}+{y}=\frac{\mathrm{7}×\mathrm{406}−\mathrm{49}×\mathrm{133}}{\mathrm{7}×\mathrm{133}−\mathrm{49}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${xy}=\frac{\mathrm{49}×\mathrm{406}−\mathrm{133}^{\mathrm{2}} }{\mathrm{7}×\mathrm{133}−\mathrm{49}^{\mathrm{2}} }=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${a}+{b}=\frac{\mathrm{7}×\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{49}}{−\frac{\mathrm{3}}{\mathrm{2}}}=\mathrm{21} \\ $$$$ \\ $$$$\:\mathrm{2014}{x}+\mathrm{2014}{y}−\mathrm{100}{a}−\mathrm{100}{b}−\mathrm{2014}{xy} \\ $$$$\:=\mathrm{2014}\left({x}+{y}−{xy}\right)−\mathrm{100}\left({a}+{b}\right) \\ $$$$\:=\mathrm{2014}\left(\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{100}×\mathrm{21} \\ $$$$\:=\mathrm{2014}×\mathrm{4}−\mathrm{100}×\mathrm{21} \\ $$$$\:=\mathrm{5956} \\ $$
Commented by mr W last updated on 26/Oct/21

$${for}\:{details}\:{see}\:{Q}\mathrm{87533} \\ $$
Commented by cortano last updated on 26/Oct/21

$${amazing}\: \\ $$
