Question Number 189825 by TUN last updated on 22/Mar/23
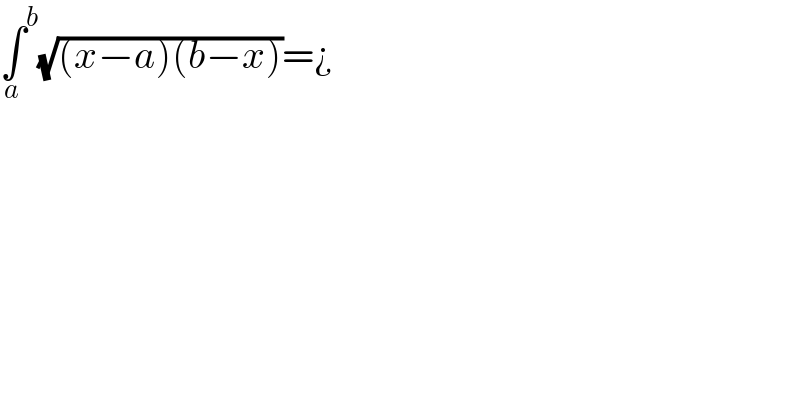
$$\underset{{a}} {\int}^{{b}} \sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}=¿ \\ $$
Answered by Frix last updated on 14/Apr/23
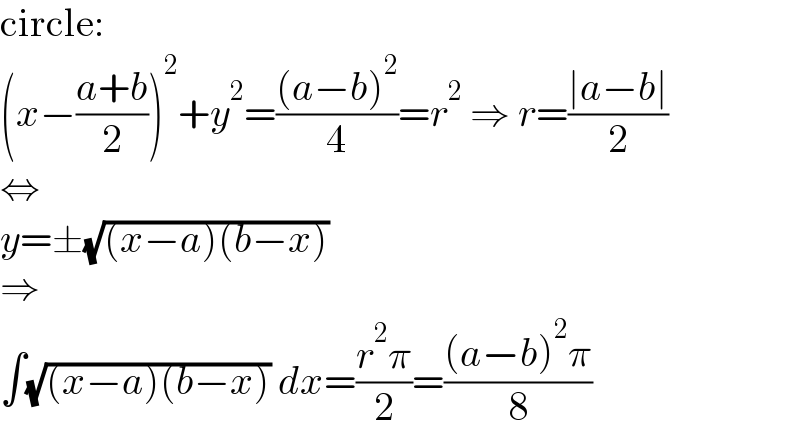
$$\mathrm{circle}: \\ $$$$\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\left({a}−{b}\right)^{\mathrm{2}} }{\mathrm{4}}={r}^{\mathrm{2}} \:\Rightarrow\:{r}=\frac{\mid{a}−{b}\mid}{\mathrm{2}} \\ $$$$\Leftrightarrow \\ $$$${y}=\pm\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)} \\ $$$$\Rightarrow \\ $$$$\int\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}\:{dx}=\frac{{r}^{\mathrm{2}} \pi}{\mathrm{2}}=\frac{\left({a}−{b}\right)^{\mathrm{2}} \pi}{\mathrm{8}} \\ $$
Answered by Mathspace last updated on 24/Mar/23
![(√(x−a))=t⇒x−a=t^2 ⇒x=t^2 +a I=∫_0 ^(√(b−a)) t(√(b−a−t^2 ))(2t)dt =2∫_0 ^(√(b−a)) t^2 (√(b−a−t^2 ))dt =_(t=(√(b−a))y) 2∫_0 ^1 (b−a)y^2 (√(b−a))(√(1−y^2 ))(√(b−a))dy =2(b−a)^2 ∫_0 ^1 y^2 (√(1−y^2 ))dy ∫_0 ^1 y^2 (√(1−y^2 ))dy=_(y=sint) ∫_0 ^(π/2) sin^2 tcost cost dt =∫_0 ^(π/2) (sint cost)^2 dt =(1/4)∫_0 ^(π/2) sin^2 (2t)dt =(1/4)∫_0 ^(π/2) ((1−cos(4t))/2)dt =(1/8).(π/2)−(1/(8.4))[sin(4t)]_0 ^(π/2) (→0) =(π/(16)) ⇒I=2(b−a)^2 .(π/(16)) =(π/8)(b−a)^2 here we have supposed a≤b](https://www.tinkutara.com/question/Q189936.png)
$$\sqrt{{x}−{a}}={t}\Rightarrow{x}−{a}={t}^{\mathrm{2}} \:\Rightarrow{x}={t}^{\mathrm{2}} +{a} \\ $$$${I}=\int_{\mathrm{0}} ^{\sqrt{{b}−{a}}} \:\:{t}\sqrt{{b}−{a}−{t}^{\mathrm{2}} }\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{{b}−{a}}} {t}^{\mathrm{2}} \sqrt{{b}−{a}−{t}^{\mathrm{2}} }{dt} \\ $$$$=_{{t}=\sqrt{{b}−{a}}{y}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left({b}−{a}\right){y}^{\mathrm{2}} \sqrt{{b}−{a}}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\sqrt{{b}−{a}}{dy} \\ $$$$=\mathrm{2}\left({b}−{a}\right)^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\mathrm{2}} \sqrt{\mathrm{1}−{y}^{\mathrm{2}} }{dy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\mathrm{2}} \sqrt{\mathrm{1}−{y}^{\mathrm{2}} }{dy}=_{{y}={sint}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {tcost}\:{cost}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\:{cost}\right)^{\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−{cos}\left(\mathrm{4}{t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}.\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}.\mathrm{4}}\left[{sin}\left(\mathrm{4}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\rightarrow\mathrm{0}\right) \\ $$$$=\frac{\pi}{\mathrm{16}}\:\Rightarrow{I}=\mathrm{2}\left({b}−{a}\right)^{\mathrm{2}} .\frac{\pi}{\mathrm{16}} \\ $$$$=\frac{\pi}{\mathrm{8}}\left({b}−{a}\right)^{\mathrm{2}} \\ $$$${here}\:{we}\:{have}\:{supposed}\:{a}\leqslant{b} \\ $$
