Menu Close

b-n-2-b-n-3-b-n-4-3-3n-3-geometric-series-b-8-

Tinku Tara 0 Comments
Pin




Question Number 146943 by mathdanisur last updated on 16/Jul/21
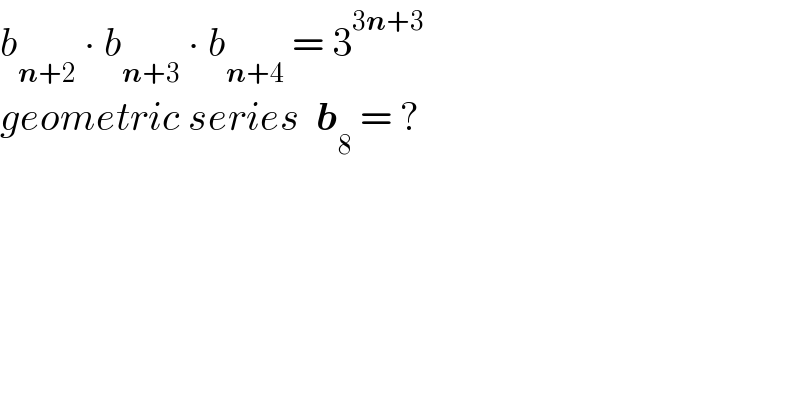
b_(n+2) ∙ b_(n+3) ∙ b_(n+4) = 3^(3n+3) geometric series b_8 = ?
$${b}_{\boldsymbol{{n}}+\mathrm{2}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{3}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{4}} \:=\:\mathrm{3}^{\mathrm{3}\boldsymbol{{n}}+\mathrm{3}} \\ $$$${geometric}\:{series}\:\:\boldsymbol{{b}}_{\mathrm{8}} \:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 16/Jul/21
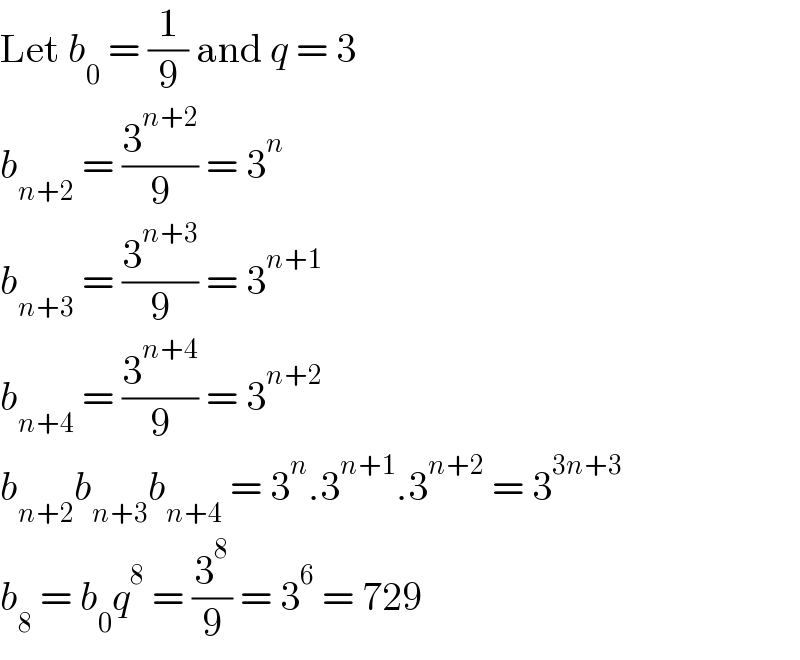
Let b_0 = (1/9) and q = 3 b_(n+2) = (3^(n+2) /9) = 3^n b_(n+3) = (3^(n+3) /9) = 3^(n+1) b_(n+4) = (3^(n+4) /9) = 3^(n+2) b_(n+2) b_(n+3) b_(n+4) = 3^n .3^(n+1) .3^(n+2) = 3^(3n+3) b_8 = b_0 q^8 = (3^8 /9) = 3^6 = 729
$$\mathrm{Let}\:{b}_{\mathrm{0}} \:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{and}\:{q}\:=\:\mathrm{3} \\ $$$${b}_{{n}+\mathrm{2}} \:=\:\frac{\mathrm{3}^{{n}+\mathrm{2}} }{\mathrm{9}}\:=\:\mathrm{3}^{{n}} \\ $$$${b}_{{n}+\mathrm{3}} \:=\:\frac{\mathrm{3}^{{n}+\mathrm{3}} }{\mathrm{9}}\:=\:\mathrm{3}^{{n}+\mathrm{1}} \\ $$$${b}_{{n}+\mathrm{4}} \:=\:\frac{\mathrm{3}^{{n}+\mathrm{4}} }{\mathrm{9}}\:=\:\mathrm{3}^{{n}+\mathrm{2}} \\ $$$${b}_{{n}+\mathrm{2}} {b}_{{n}+\mathrm{3}} {b}_{{n}+\mathrm{4}} \:=\:\mathrm{3}^{{n}} .\mathrm{3}^{{n}+\mathrm{1}} .\mathrm{3}^{{n}+\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{3}{n}+\mathrm{3}} \\ $$$${b}_{\mathrm{8}} \:=\:{b}_{\mathrm{0}} {q}^{\mathrm{8}} \:=\:\frac{\mathrm{3}^{\mathrm{8}} }{\mathrm{9}}\:=\:\mathrm{3}^{\mathrm{6}} \:=\:\mathrm{729} \\ $$
Commented by mathdanisur last updated on 16/Jul/21
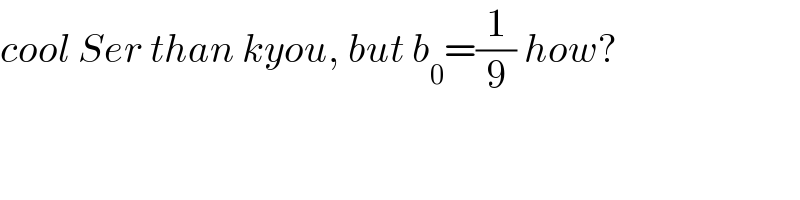
cool Ser than kyou, but b_0 =(1/9) how?
$${cool}\:{Ser}\:{than}\:{kyou},\:{but}\:{b}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{9}}\:{how}? \\ $$
Answered by Rasheed.Sindhi last updated on 17/Jul/21
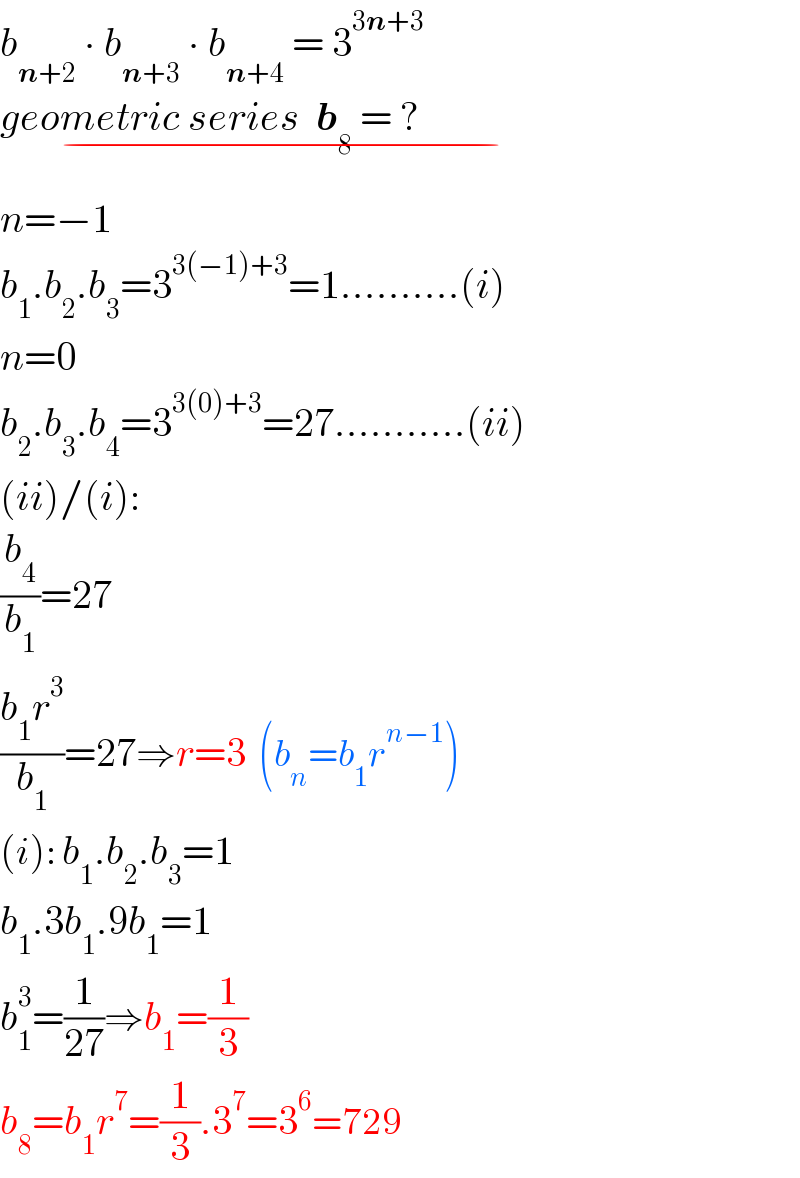
b_(n+2) ∙ b_(n+3) ∙ b_(n+4) = 3^(3n+3) geometric series b_8 = ? _(−) n=−1 b_1 .b_2 .b_3 =3^(3(−1)+3) =1..........(i) n=0 b_2 .b_3 .b_4 =3^(3(0)+3) =27...........(ii) (ii)/(i): (b_4 /b_1 )=27 ((b_1 r^3 )/b_1 )=27⇒r=3 (b_n =b_1 r^(n−1) ) (i): b_1 .b_2 .b_3 =1 b_1 .3b_1 .9b_1 =1 b_1 ^3 =(1/(27))⇒b_1 =(1/3) b_8 =b_1 r^7 =(1/3).3^7 =3^6 =729
$${b}_{\boldsymbol{{n}}+\mathrm{2}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{3}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{4}} \:=\:\mathrm{3}^{\mathrm{3}\boldsymbol{{n}}+\mathrm{3}} \\ $$$$\underset{−} {{geometric}\:{series}\:\:\boldsymbol{{b}}_{\mathrm{8}} \:=\:?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$${n}=−\mathrm{1} \\ $$$${b}_{\mathrm{1}} .{b}_{\mathrm{2}} .{b}_{\mathrm{3}} =\mathrm{3}^{\mathrm{3}\left(−\mathrm{1}\right)+\mathrm{3}} =\mathrm{1}……….\left({i}\right) \\ $$$${n}=\mathrm{0} \\ $$$${b}_{\mathrm{2}} .{b}_{\mathrm{3}} .{b}_{\mathrm{4}} =\mathrm{3}^{\mathrm{3}\left(\mathrm{0}\right)+\mathrm{3}} =\mathrm{27}………..\left({ii}\right) \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\frac{{b}_{\mathrm{4}} }{{b}_{\mathrm{1}} }=\mathrm{27} \\ $$$$\frac{{b}_{\mathrm{1}} {r}^{\mathrm{3}} }{{b}_{\mathrm{1}} }=\mathrm{27}\Rightarrow{r}=\mathrm{3}\:\:\left({b}_{{n}} ={b}_{\mathrm{1}} {r}^{{n}−\mathrm{1}} \right) \\ $$$$\left({i}\right):\:{b}_{\mathrm{1}} .{b}_{\mathrm{2}} .{b}_{\mathrm{3}} =\mathrm{1} \\ $$$${b}_{\mathrm{1}} .\mathrm{3}{b}_{\mathrm{1}} .\mathrm{9}{b}_{\mathrm{1}} =\mathrm{1} \\ $$$${b}_{\mathrm{1}} ^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{27}}\Rightarrow{b}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${b}_{\mathrm{8}} ={b}_{\mathrm{1}} {r}^{\mathrm{7}} =\frac{\mathrm{1}}{\mathrm{3}}.\mathrm{3}^{\mathrm{7}} =\mathrm{3}^{\mathrm{6}} =\mathrm{729} \\ $$
Commented by mathdanisur last updated on 17/Jul/21
cool Ser thankyou
$${cool}\:{Ser}\:{thankyou} \\ $$
Answered by Rasheed.Sindhi last updated on 17/Jul/21
Let b is first term and r is common ratio. determinant (((b_n =br^(n−1) ))) b_(n+2) ∙ b_(n+3) ∙ b_(n+4) = 3^(3n+3) br^(n+2-1) .br^(n+3-1) .br^(n+4-1) =3^(3n+3) br^(n+1) .br^(n+2) .br^(n+3) =3^(3n+3) b^3 r^(3n+6) =3^(3n+3) br^(n+2) =3^(n+1) ⇒ { ((n=-2 : b=(1/3))),((n=−1 : ((1/3))r=1⇒r=3)) :} b_8 =br^(8−1) =((1/3))(3)^7 =3^6 =729
$$\:\:{Let}\:{b}\:{is}\:{first}\:{term}\:{and}\:{r}\:{is}\:{common} \\ $$$$\:\:{ratio}. \\ $$$$\begin{array}{|c|}{{b}_{{n}} ={br}^{{n}−\mathrm{1}} }\\\hline\end{array} \\ $$$${b}_{\boldsymbol{{n}}+\mathrm{2}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{3}} \:\centerdot\:{b}_{\boldsymbol{{n}}+\mathrm{4}} \:=\:\mathrm{3}^{\mathrm{3}\boldsymbol{{n}}+\mathrm{3}} \\ $$$${br}^{{n}+\mathrm{2}-\mathrm{1}} .{br}^{{n}+\mathrm{3}-\mathrm{1}} .{br}^{{n}+\mathrm{4}-\mathrm{1}} =\mathrm{3}^{\mathrm{3}{n}+\mathrm{3}} \\ $$$${br}^{{n}+\mathrm{1}} .{br}^{{n}+\mathrm{2}} .{br}^{{n}+\mathrm{3}} =\mathrm{3}^{\mathrm{3}{n}+\mathrm{3}} \\ $$$${b}^{\mathrm{3}} {r}^{\mathrm{3}{n}+\mathrm{6}} =\mathrm{3}^{\mathrm{3}{n}+\mathrm{3}} \\ $$$${br}^{{n}+\mathrm{2}} =\mathrm{3}^{{n}+\mathrm{1}} \Rightarrow\begin{cases}{{n}=-\mathrm{2}\::\:{b}=\frac{\mathrm{1}}{\mathrm{3}}}\\{{n}=−\mathrm{1}\::\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right){r}=\mathrm{1}\Rightarrow{r}=\mathrm{3}}\end{cases} \\ $$$${b}_{\mathrm{8}} ={br}^{\mathrm{8}−\mathrm{1}} =\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{3}\right)^{\mathrm{7}} =\mathrm{3}^{\mathrm{6}} =\mathrm{729} \\ $$
Commented by mathdanisur last updated on 17/Jul/21
cool Ser thankyou
$${cool}\:{Ser}\:{thankyou} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *