Menu Close

be-math-1-lim-x-0-x-cos-x-sin-x-x-2-sin-x-2-find-dy-dx-from-x-y-x-y-x-2-y-2-

Tinku Tara 0 Comments
Pin




Question Number 110075 by bemath last updated on 27/Aug/20
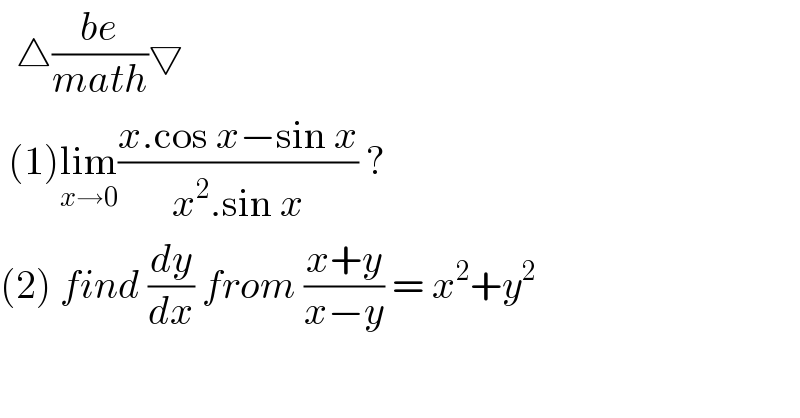
△((be)/(math))▽ (1)lim_(x→0) ((x.cos x−sin x)/(x^2 .sin x)) ? (2) find (dy/dx) from ((x+y)/(x−y)) = x^2 +y^2
$$\:\:\bigtriangleup\frac{{be}}{{math}}\bigtriangledown \\ $$$$\:\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}.\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} .\mathrm{sin}\:{x}}\:? \\ $$$$\left(\mathrm{2}\right)\:{find}\:\frac{{dy}}{{dx}}\:{from}\:\frac{{x}+{y}}{{x}−{y}}\:=\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$
Commented by bobhans last updated on 27/Aug/20
(((bob)/(hans))) (d/dx)[((x+y)/(x−y))] = (d/dx)[x^2 +y^2 ] (((1+y′)(x−y)−(x+y)(1−y′))/((x−y)^2 ))=2x+2y′ ((x−y+xy′−yy′−x+xy′−y+yy′)/((x−y)^2 ))=2x+2y′ ((2xy′−2y)/((x−y)^2 )) = 2x+2y′⇒ xy′−y=(x+y′)(x−y)^2 xy′−y′(x−y)^2 =y+x(x−y)^2 y′=((y+x(x−y)^2 )/(x−(x−y)^2 )). ♥
$$\left(\frac{{bob}}{{hans}}\right)\:\frac{{d}}{{dx}}\left[\frac{{x}+{y}}{{x}−{y}}\right]\:=\:\frac{{d}}{{dx}}\left[{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\right] \\ $$$$\frac{\left(\mathrm{1}+{y}'\right)\left({x}−{y}\right)−\left({x}+{y}\right)\left(\mathrm{1}−{y}'\right)}{\left({x}−{y}\right)^{\mathrm{2}} }=\mathrm{2}{x}+\mathrm{2}{y}' \\ $$$$\frac{{x}−{y}+{xy}'−{yy}'−{x}+{xy}'−{y}+{yy}'}{\left({x}−{y}\right)^{\mathrm{2}} }=\mathrm{2}{x}+\mathrm{2}{y}' \\ $$$$\frac{\mathrm{2}{xy}'−\mathrm{2}{y}}{\left({x}−{y}\right)^{\mathrm{2}} }\:=\:\mathrm{2}{x}+\mathrm{2}{y}'\Rightarrow\:{xy}'−{y}=\left({x}+{y}'\right)\left({x}−{y}\right)^{\mathrm{2}} \\ $$$${xy}'−{y}'\left({x}−{y}\right)^{\mathrm{2}} ={y}+{x}\left({x}−{y}\right)^{\mathrm{2}} \\ $$$${y}'=\frac{{y}+{x}\left({x}−{y}\right)^{\mathrm{2}} }{{x}−\left({x}−{y}\right)^{\mathrm{2}} }.\:\heartsuit \\ $$
Commented by bemath last updated on 27/Aug/20
Answered by john santu last updated on 27/Aug/20
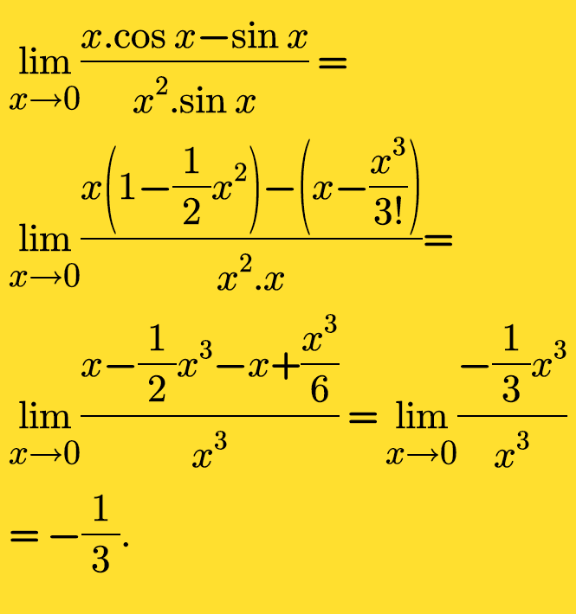
Answered by 1549442205PVT last updated on 27/Aug/20
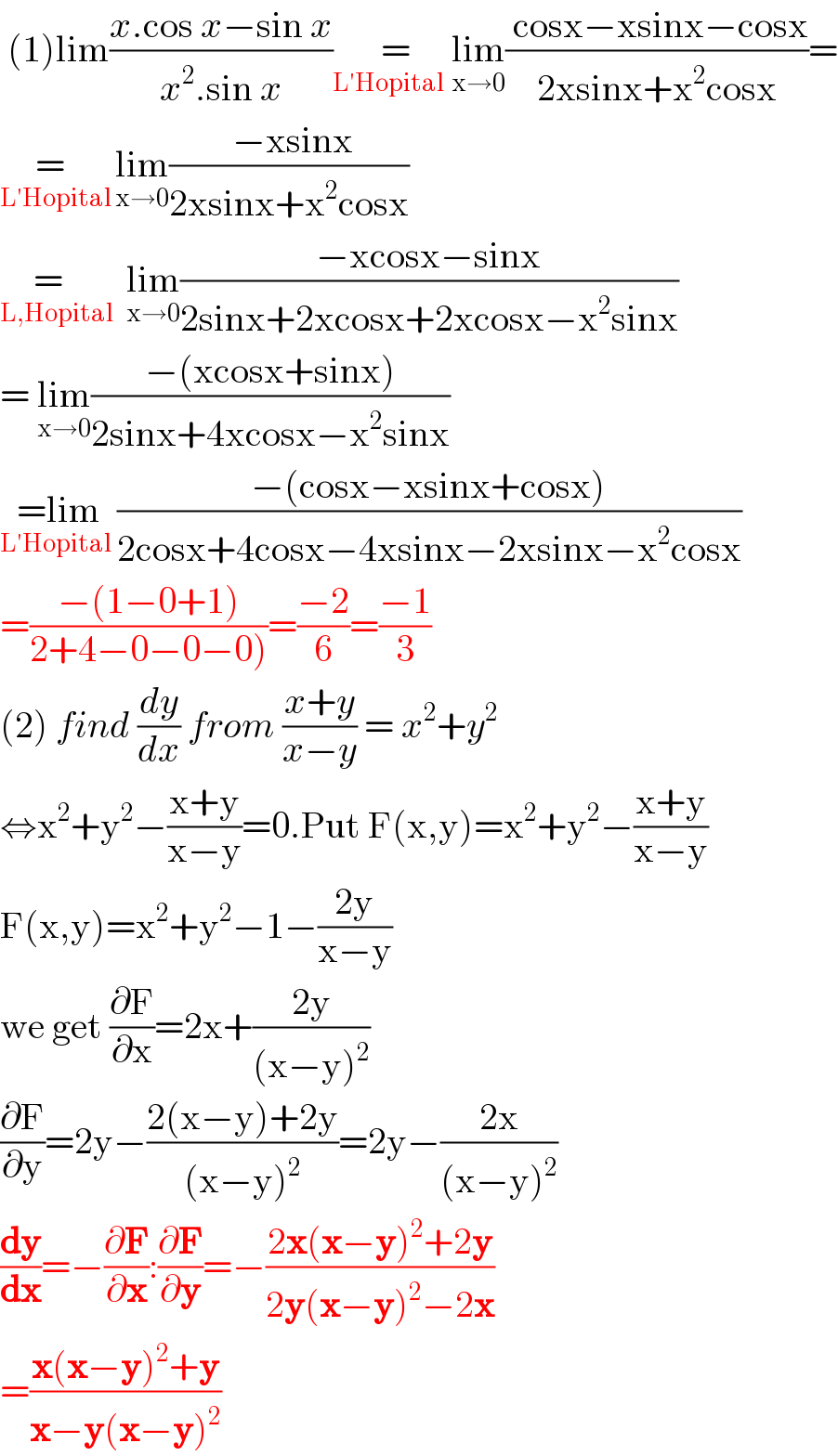
(1)lim((x.cos x−sin x)/(x^2 .sin x)) =_(L′Hopital ) lim_(x→0) (( cosx−xsinx−cosx)/(2xsinx+x^2 cosx))= = _(L′Hopital ) lim_(x→0) (( −xsinx)/(2xsinx+x^2 cosx)) = _(L,Hopital) lim_(x→0) ((−xcosx−sinx)/(2sinx+2xcosx+2xcosx−x^2 sinx)) = lim_(x→0) ((−(xcosx+sinx))/(2sinx+4xcosx−x^2 sinx)) =lim_(L′Hopital ) ((−(cosx−xsinx+cosx))/(2cosx+4cosx−4xsinx−2xsinx−x^2 cosx)) =((−(1−0+1))/(2+4−0−0−0)))=((−2)/6)=((−1)/3) (2) find (dy/dx) from ((x+y)/(x−y)) = x^2 +y^2 ⇔x^2 +y^2 −((x+y)/(x−y))=0.Put F(x,y)=x^2 +y^2 −((x+y)/(x−y)) F(x,y)=x^2 +y^2 −1−((2y)/(x−y)) we get (∂F/∂x)=2x+((2y)/((x−y)^2 )) (∂F/∂y)=2y−((2(x−y)+2y)/((x−y)^2 ))=2y−((2x)/((x−y)^2 )) (dy/dx)=−(∂F/∂x):(∂F/∂y)=−((2x(x−y)^2 +2y)/(2y(x−y)^2 −2x)) =((x(x−y)^2 +y)/(x−y(x−y)^2 ))
$$\:\left(\mathrm{1}\right)\mathrm{lim}\frac{{x}.\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} .\mathrm{sin}\:{x}}\underset{\mathrm{L}'\mathrm{Hopital}\:\:} {\:=}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\:\mathrm{cosx}−\mathrm{xsinx}−\mathrm{cosx}}{\mathrm{2xsinx}+\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}= \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}\:} {=\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\:−\mathrm{xsinx}}{\mathrm{2xsinx}+\mathrm{x}^{\mathrm{2}} \mathrm{cosx}} \\ $$$$\underset{\mathrm{L},\mathrm{Hopital}} {=\:\:}\:\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{xcosx}−\mathrm{sinx}}{\mathrm{2sinx}+\mathrm{2xcosx}+\mathrm{2xcosx}−\mathrm{x}^{\mathrm{2}} \mathrm{sinx}} \\ $$$$=\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\left(\mathrm{xcosx}+\mathrm{sinx}\right)}{\mathrm{2sinx}+\mathrm{4xcosx}−\mathrm{x}^{\mathrm{2}} \mathrm{sinx}} \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}\:\:} {=\mathrm{lim}}\frac{−\left(\mathrm{cosx}−\mathrm{xsinx}+\mathrm{cosx}\right)}{\mathrm{2cosx}+\mathrm{4cosx}−\mathrm{4xsinx}−\mathrm{2xsinx}−\mathrm{x}^{\mathrm{2}} \mathrm{cosx}} \\ $$$$=\frac{−\left(\mathrm{1}−\mathrm{0}+\mathrm{1}\right)}{\left.\mathrm{2}+\mathrm{4}−\mathrm{0}−\mathrm{0}−\mathrm{0}\right)}=\frac{−\mathrm{2}}{\mathrm{6}}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:{find}\:\frac{{dy}}{{dx}}\:{from}\:\frac{{x}+{y}}{{x}−{y}}\:=\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}=\mathrm{0}.\mathrm{Put}\:\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{1}−\frac{\mathrm{2y}}{\mathrm{x}−\mathrm{y}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\partial\mathrm{F}}{\partial\mathrm{x}}=\mathrm{2x}+\frac{\mathrm{2y}}{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial\mathrm{F}}{\partial\mathrm{y}}=\mathrm{2y}−\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{y}\right)+\mathrm{2y}}{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} }=\mathrm{2y}−\frac{\mathrm{2x}}{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} } \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=−\frac{\partial\boldsymbol{\mathrm{F}}}{\partial\boldsymbol{\mathrm{x}}}:\frac{\partial\boldsymbol{\mathrm{F}}}{\partial\boldsymbol{\mathrm{y}}}=−\frac{\mathrm{2}\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{y}}}{\mathrm{2}\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}} \\ $$$$=\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *