Question Number 110072 by bemath last updated on 27/Aug/20
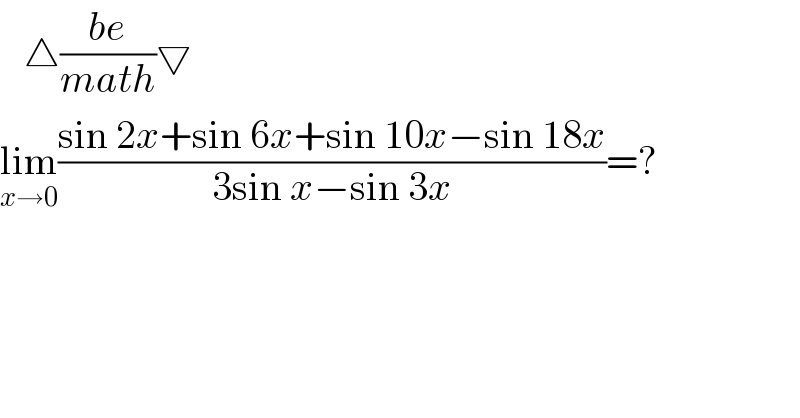
$$\:\:\:\bigtriangleup\frac{{be}}{{math}}\bigtriangledown \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{2}{x}+\mathrm{sin}\:\mathrm{6}{x}+\mathrm{sin}\:\mathrm{10}{x}−\mathrm{sin}\:\mathrm{18}{x}}{\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}}=? \\ $$
Answered by john santu last updated on 27/Aug/20

Commented by bemath last updated on 27/Aug/20
$${waw}…{very}\:{clear}\:{explanation} \\ $$
Commented by bemath last updated on 27/Aug/20

Answered by 1549442205PVT last updated on 27/Aug/20

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{2}{x}+\mathrm{sin}\:\mathrm{6}{x}+\mathrm{sin}\:\mathrm{10}{x}−\mathrm{sin}\:\mathrm{18}{x}}{\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}}= \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}} {=\:}\frac{\mathrm{2cos2x}+\mathrm{6cos6x}+\mathrm{10cos10x}−\mathrm{18cos18x}}{\mathrm{3cosx}−\mathrm{3cos3x}} \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}\:} {=\:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{4sin2x}−\mathrm{36sin6x}−\mathrm{100sin10x}+\mathrm{324sin18x}}{−\mathrm{3sinx}+\mathrm{9sin3x}} \\ $$$$\overset{\mathrm{L}'\mathrm{Hopital}} {\:=\:}\:\mathrm{lim}\frac{−\left(\mathrm{8cos2x}+\mathrm{216cos6x}+\mathrm{1000cos10x}−\mathrm{5832cos18x}\right)}{−\mathrm{3cosx}+\mathrm{27cos3x}} \\ $$$$=\frac{−\left(\mathrm{8}+\mathrm{216}+\mathrm{1000}−\mathrm{5832}\right)}{\mathrm{24}}=\frac{\mathrm{4608}}{\mathrm{24}}=\mathrm{192} \\ $$
