be-math-lim-x-0-x-2-cos-1-x-

Question Number 110095 by bemath last updated on 27/Aug/20

$$\:\:\:\left[\frac{{be}}{{math}}\right] \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right) \\ $$

Answered by john santu last updated on 27/Aug/20

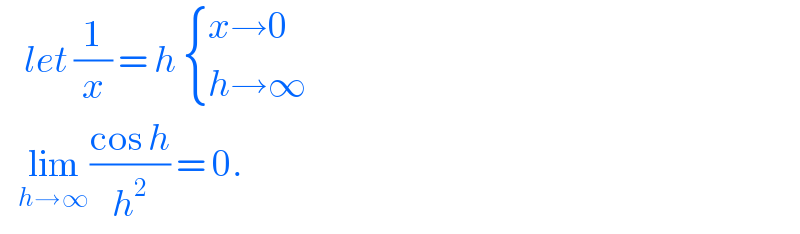
let (1/x) = h { ((x→0)),((h→∞)) :} lim_(h→∞) ((cos h)/h^2 ) = 0.

$$\:\:\:\:{let}\:\frac{\mathrm{1}}{{x}}\:=\:{h}\:\begin{cases}{{x}\rightarrow\mathrm{0}}\\{{h}\rightarrow\infty}\end{cases} \\ $$$$\:\:\:\underset{{h}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:{h}}{{h}^{\mathrm{2}} }\:=\:\mathrm{0}. \\ $$

Answered by 1549442205PVT last updated on 27/Aug/20

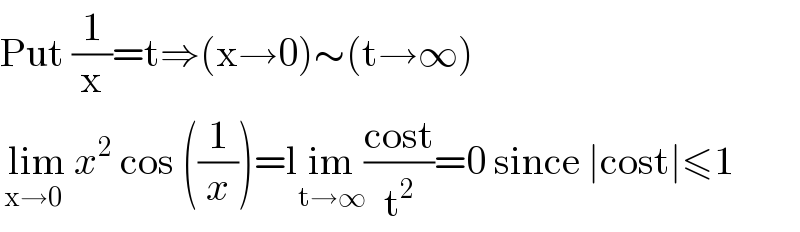
Put (1/x)=t⇒(x→0)∼(t→∞) lim_(x→0) x^2 cos ((1/x))=lim_(t→∞) ((cost)/t^2 )=0 since ∣cost∣≤1

$$\mathrm{Put}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\Rightarrow\left(\mathrm{x}\rightarrow\mathrm{0}\right)\sim\left(\mathrm{t}\rightarrow\infty\right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\:\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{l}\underset{\mathrm{t}\rightarrow\infty} {\mathrm{im}}\frac{\mathrm{cost}}{\mathrm{t}^{\mathrm{2}} }=\mathrm{0}\:\mathrm{since}\:\mid\mathrm{cost}\mid\leqslant\mathrm{1} \\ $$

Answered by Rio Michael last updated on 27/Aug/20

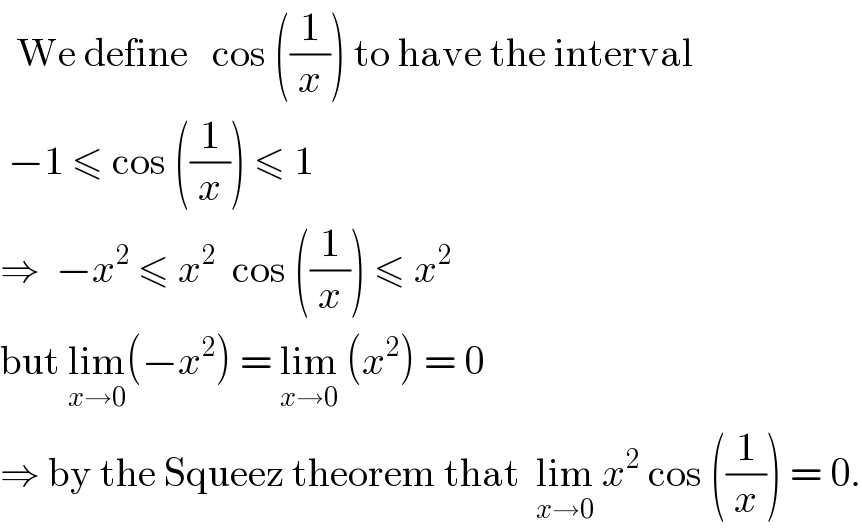
We define cos ((1/x)) to have the interval −1 ≤ cos ((1/x)) ≤ 1 ⇒ −x^2 ≤ x^2 cos ((1/x)) ≤ x^2 but lim_(x→0) (−x^2 ) = lim_(x→0) (x^2 ) = 0 ⇒ by the Squeez theorem that lim_(x→0) x^2 cos ((1/x)) = 0.

$$\:\:\mathrm{We}\:\mathrm{define}\:\:\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:\mathrm{to}\:\mathrm{have}\:\mathrm{the}\:\mathrm{interval} \\ $$$$\:−\mathrm{1}\:\leqslant\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:\:−{x}^{\mathrm{2}} \:\leqslant\:{x}^{\mathrm{2}} \:\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:\leqslant\:{x}^{\mathrm{2}} \\ $$$$\mathrm{but}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−{x}^{\mathrm{2}} \right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left({x}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{by}\:\mathrm{the}\:\mathrm{Squeez}\:\mathrm{theorem}\:\mathrm{that}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{0}. \\ $$

Facebook Tweet Pin

be-math-lim-x-0-x-2-cos-1-x-

Leave a Reply Cancel reply