Question Number 107923 by bemath last updated on 13/Aug/20
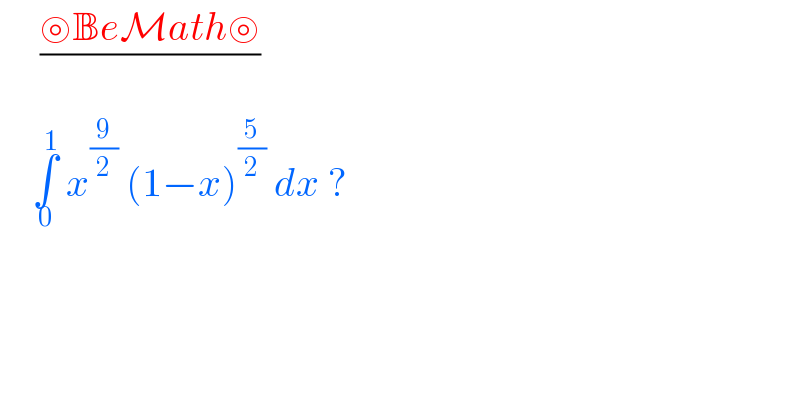
$$\:\:\:\:\:\frac{\circledcirc\mathbb{B}{e}\mathcal{M}{ath}\circledcirc}{} \\ $$$$\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{\frac{\mathrm{9}}{\mathrm{2}}} \:\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:{dx}\:? \\ $$
Answered by 1549442205PVT last updated on 13/Aug/20
![Set (1/x)−1=t^2 ⇒−(1/x^2 )dx=2tdt⇒dx=−2tx^2 dt t(x=1)=0,t(x=0)=∞ x=(1/( (√(1+t^2 ))))⇒I=∫_0 ^∞ x^(9/2) (xt^2 )^(1/2) 2tx^2 dt =2∫_0 ^∞ x^7 t^2 dt=2∫_0 ^∞ ((t^2 dt)/( (√((1+t^2 )^7 )))) =2∫_1 ^∞ ((t^2 +1−1)/((1+t^2 )^3 (√(1+t^2 ))))dt=2∫(dt/((1+t^2 )^2 (√(1+t^2 )))) −2∫_0 ^∞ (dt/((1+t^2 )^3 (√(1+t^2 ))))= Set t=tanϕ⇒dt=(1+t^2 )dϕ I=2∫_0 ^(π/2) (dϕ/((1+tan^2 ϕ)(√(1+tan^2 ϕ))))) −2∫_0 ^(π/2) (dϕ/((1+tan^2 ϕ)^2 (√(1+tan^2 ϕ))))) =2∫_0 ^(π/2) cos^3 ϕdϕ−2∫_0 ^(π/2) cos^5 dϕ =2∫_0 ^(π/2) (1−sin^2 ϕ)dsinϕ−2∫_0 ^(π/2) (1−sin^2 ϕ)^2 dsinϕ =(2sinϕ−((2sin^3 ϕ)/3))∣_0 ^(π/2) −2∫_0 ^(π/2) [1−2sin^2 ϕ+sin^4 ϕ)dsinϕ =2−(2/3)−2[sinϕ−(2/3)sin^3 ϕ+((sin^5 ϕ)/5)]_0 ^(π/2) =2−(2/3)−2(1−(2/3)+(1/5))=(4/(15))](https://www.tinkutara.com/question/Q107961.png)
$$\mathrm{Set}\:\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}=\mathrm{t}^{\mathrm{2}} \Rightarrow−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{2tdt}\Rightarrow\mathrm{dx}=−\mathrm{2tx}^{\mathrm{2}} \mathrm{dt} \\ $$$$\mathrm{t}\left(\mathrm{x}=\mathrm{1}\right)=\mathrm{0},\mathrm{t}\left(\mathrm{x}=\mathrm{0}\right)=\infty \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\frac{\mathrm{9}}{\mathrm{2}}} \left(\mathrm{xt}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2tx}^{\mathrm{2}} \mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{7}} \mathrm{t}^{\mathrm{2}} \mathrm{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} \mathrm{dt}}{\:\sqrt{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{7}} }} \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\mathrm{2}\int\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }} \\ $$$$−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}= \\ $$$$\mathrm{Set}\:\mathrm{t}=\mathrm{tan}\varphi\Rightarrow\mathrm{dt}=\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{d}\varphi \\ $$$$\mathrm{I}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{d}\varphi}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \varphi\right)\sqrt{\left.\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \varphi\right)}} \\ $$$$−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{d}\varphi}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \varphi\right)^{\mathrm{2}} \sqrt{\left.\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \varphi\right)}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{3}} \varphi\mathrm{d}\varphi−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{5}} \mathrm{d}\varphi \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \varphi\right)\mathrm{dsin}\varphi−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \varphi\right)^{\mathrm{2}} \mathrm{dsin}\varphi \\ $$$$=\left(\mathrm{2sin}\varphi−\frac{\mathrm{2sin}^{\mathrm{3}} \varphi}{\mathrm{3}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \varphi+\mathrm{sin}^{\mathrm{4}} \varphi\right)\mathrm{dsin}\varphi \\ $$$$=\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\left[\mathrm{sin}\varphi−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}^{\mathrm{3}} \varphi+\frac{\mathrm{sin}^{\mathrm{5}} \varphi}{\mathrm{5}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}\right)=\frac{\mathrm{4}}{\mathrm{15}} \\ $$
Answered by bobhans last updated on 13/Aug/20
![((BobHans)/Π) I=−(2/7)∫_0 ^1 x^(9/2) d(1−x)^(7/2) = −(2/7)[ x^(9/2) (1−x)^(7/2) ]_0 ^1 + (9/7)∫_0 ^1 x^(7/2) (1−x)^(7/2) dx let J = ∫_0 ^1 x^(7/2) (1−x)^(7/2) dx=(9/7)∫_0 ^1 (x−x^2 )^(7/2) dx J=(9/7)∫_0 ^1 [ (1/4)−((1/2)−x)^2 ]^(7/2) dx set (1/2)−x = z J=(9/(7×2^8 )) ∫_(−π/2) ^(π/2) cos^8 z dz Reduction formula J_n = ((n−1)/n).J_(n−2) ⇒J_8 = (7/8).(5/6).(3/4).(1/2).J_0 J_8 = ((35)/(128)).[(π/2)−(−(π/2))]= ((35π)/(128)) conclusion I= (9/(7×2^8 )) ×((35π)/(128)) = ((45π)/(32768)).](https://www.tinkutara.com/question/Q107963.png)
$$\:\:\:\:\frac{\nshortparallel\mathcal{B}\mathrm{ob}\mathcal{H}\mathrm{ans}\nshortparallel}{\Pi} \\ $$$$\mathrm{I}=−\frac{\mathrm{2}}{\mathrm{7}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{9}/\mathrm{2}} \:\mathrm{d}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{7}/\mathrm{2}} \:=\:−\frac{\mathrm{2}}{\mathrm{7}}\left[\:\mathrm{x}^{\mathrm{9}/\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{7}/\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} + \\ $$$$\frac{\mathrm{9}}{\mathrm{7}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{7}/\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{7}/\mathrm{2}} \:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{J}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{7}/\mathrm{2}} \:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{7}/\mathrm{2}} \:\mathrm{dx}=\frac{\mathrm{9}}{\mathrm{7}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{7}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\mathrm{J}=\frac{\mathrm{9}}{\mathrm{7}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left[\:\frac{\mathrm{1}}{\mathrm{4}}−\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{x}\right)^{\mathrm{2}} \:\right]^{\mathrm{7}/\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{set}\:\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{x}\:=\:\mathrm{z}\: \\ $$$$\mathrm{J}=\frac{\mathrm{9}}{\mathrm{7}×\mathrm{2}^{\mathrm{8}} }\:\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\:\mathrm{cos}\:^{\mathrm{8}} \:\mathrm{z}\:\mathrm{dz}\:\: \\ $$$$\mathrm{Reduction}\:\mathrm{formula}\: \\ $$$$\mathrm{J}_{\mathrm{n}} \:=\:\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}}.\mathrm{J}_{\mathrm{n}−\mathrm{2}} \:\Rightarrow\mathrm{J}_{\mathrm{8}} =\:\frac{\mathrm{7}}{\mathrm{8}}.\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{J}_{\mathrm{0}} \\ $$$$\mathrm{J}_{\mathrm{8}} =\:\frac{\mathrm{35}}{\mathrm{128}}.\left[\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right]=\:\frac{\mathrm{35}\pi}{\mathrm{128}} \\ $$$$\mathrm{conclusion}\: \\ $$$$\mathrm{I}=\:\frac{\mathrm{9}}{\mathrm{7}×\mathrm{2}^{\mathrm{8}} }\:×\frac{\mathrm{35}\pi}{\mathrm{128}}\:=\:\frac{\mathrm{45}\pi}{\mathrm{32768}}.\: \\ $$$$ \\ $$
Commented by bemath last updated on 14/Aug/20
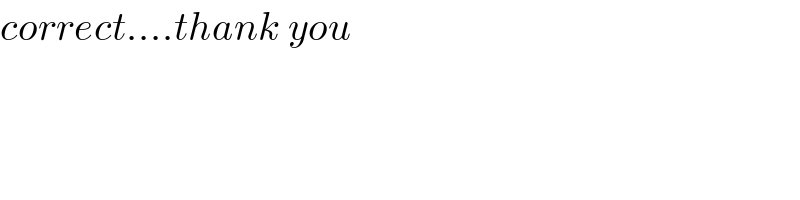
$${correct}….{thank}\:{you} \\ $$
Answered by mathmax by abdo last updated on 13/Aug/20
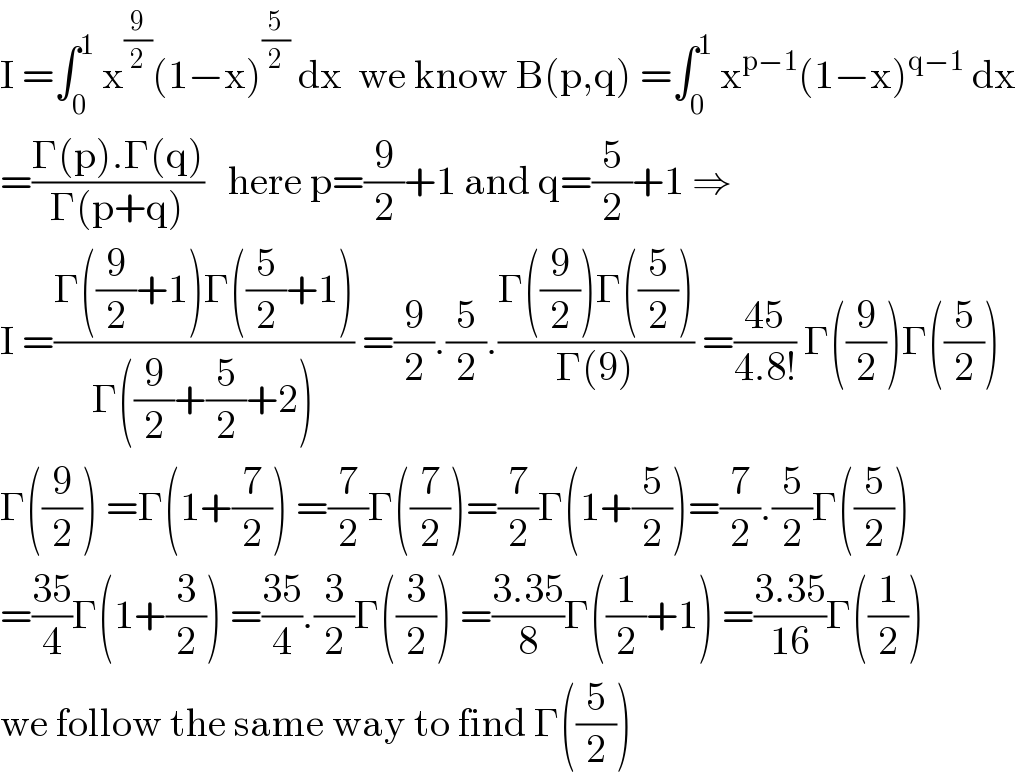
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\frac{\mathrm{9}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{x}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{p}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{q}−\mathrm{1}} \:\mathrm{dx} \\ $$$$=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)}\:\:\:\mathrm{here}\:\mathrm{p}=\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{1}\:\mathrm{and}\:\mathrm{q}=\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{1}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}\right)}{\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{2}\right)}\:=\frac{\mathrm{9}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{9}\right)}\:=\frac{\mathrm{45}}{\mathrm{4}.\mathrm{8}!}\:\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\:=\Gamma\left(\mathrm{1}+\frac{\mathrm{7}}{\mathrm{2}}\right)\:=\frac{\mathrm{7}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{2}}\Gamma\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{35}}{\mathrm{4}}\Gamma\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{35}}{\mathrm{4}}.\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{3}.\mathrm{35}}{\mathrm{8}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{3}.\mathrm{35}}{\mathrm{16}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{we}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way}\:\mathrm{to}\:\mathrm{find}\:\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$
Commented by bemath last updated on 14/Aug/20
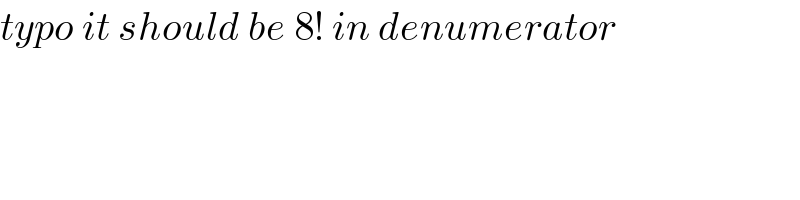
$${typo}\:{it}\:{should}\:{be}\:\mathrm{8}!\:{in}\:{denumerator} \\ $$
