Menu Close

bemath-0-2pi-ln-1-sin-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 107314 by bemath last updated on 10/Aug/20
⌆bemath⌆ ∫_0 ^(2π) ln (1+sin x) dx ?
$$\:\:\:\:\:\:\:\:\doublebarwedge{bemath}\doublebarwedge \\ $$$$\:\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\:{dx}\:? \\ $$
Answered by mnjuly1970 last updated on 10/Aug/20
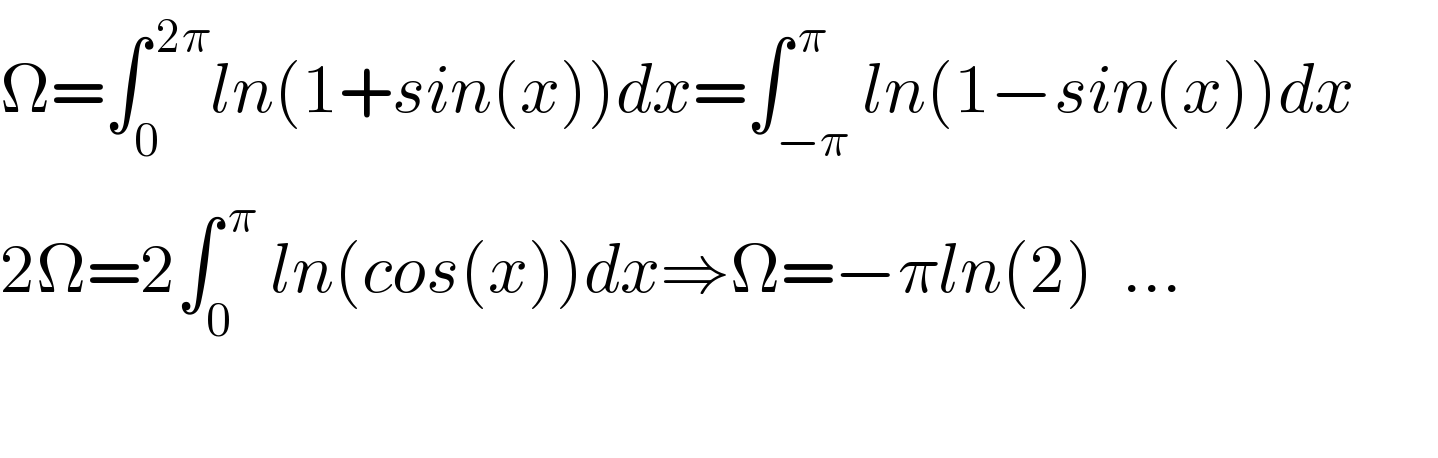
Ω=∫_0 ^( 2π) ln(1+sin(x))dx=∫_(−π) ^( π) ln(1−sin(x))dx 2Ω=2∫_0 ^( π) ln(cos(x))dx⇒Ω=−πln(2) ...
$$\Omega=\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} {ln}\left(\mathrm{1}+{sin}\left({x}\right)\right){dx}=\int_{−\pi} ^{\:\pi} {ln}\left(\mathrm{1}−{sin}\left({x}\right)\right){dx}\:\:\:\:\:\: \\ $$$$\mathrm{2}\Omega=\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \:{ln}\left({cos}\left({x}\right)\right){dx}\Rightarrow\Omega=−\pi{ln}\left(\mathrm{2}\right)\:\:… \\ $$$$\:\: \\ $$
Commented by bemath last updated on 10/Aug/20
thank you
$${thank}\:{you} \\ $$
Answered by mathmax by abdo last updated on 10/Aug/20
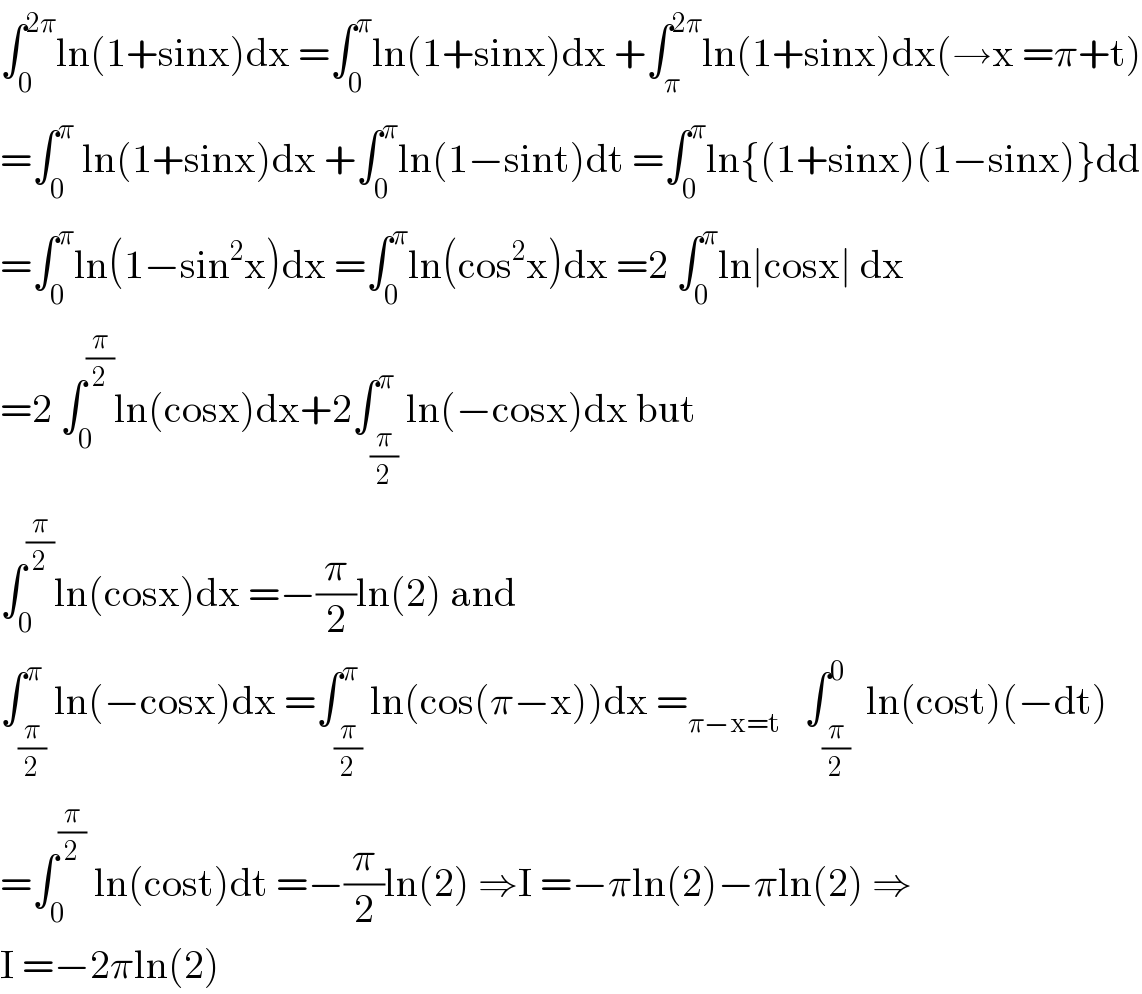
∫_0 ^(2π) ln(1+sinx)dx =∫_0 ^π ln(1+sinx)dx +∫_π ^(2π) ln(1+sinx)dx(→x =π+t) =∫_0 ^π ln(1+sinx)dx +∫_0 ^π ln(1−sint)dt =∫_0 ^π ln{(1+sinx)(1−sinx)}dd =∫_0 ^π ln(1−sin^2 x)dx =∫_0 ^π ln(cos^2 x)dx =2 ∫_0 ^π ln∣cosx∣ dx =2 ∫_0 ^(π/2) ln(cosx)dx+2∫_(π/2) ^π ln(−cosx)dx but ∫_0 ^(π/2) ln(cosx)dx =−(π/2)ln(2) and ∫_(π/2) ^π ln(−cosx)dx =∫_(π/2) ^π ln(cos(π−x))dx =_(π−x=t) ∫_(π/2) ^0 ln(cost)(−dt) =∫_0 ^(π/2) ln(cost)dt =−(π/2)ln(2) ⇒I =−πln(2)−πln(2) ⇒ I =−2πln(2)
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\mathrm{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\mathrm{dx}\left(\rightarrow\mathrm{x}\:=\pi+\mathrm{t}\right) \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\mathrm{dx}\:+\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}−\mathrm{sint}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left\{\left(\mathrm{1}+\mathrm{sinx}\right)\left(\mathrm{1}−\mathrm{sinx}\right)\right\}\mathrm{dd} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\mid\mathrm{cosx}\mid\:\mathrm{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}\right)\mathrm{dx}+\mathrm{2}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{ln}\left(−\mathrm{cosx}\right)\mathrm{dx}\:\mathrm{but}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}\right)\mathrm{dx}\:=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:\mathrm{and} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{ln}\left(−\mathrm{cosx}\right)\mathrm{dx}\:=\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{ln}\left(\mathrm{cos}\left(\pi−\mathrm{x}\right)\right)\mathrm{dx}\:=_{\pi−\mathrm{x}=\mathrm{t}} \:\:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \:\mathrm{ln}\left(\mathrm{cost}\right)\left(−\mathrm{dt}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cost}\right)\mathrm{dt}\:=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{I}\:=−\pi\mathrm{ln}\left(\mathrm{2}\right)−\pi\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *