Menu Close

BeMath-1-0-x-1-x-3-dx-2-lim-x-0-sin-pi-cos-2-x-x-2-3-If-g-x-1-x-and-g-f-x-3-2-x-x-find-f-x-

Tinku Tara 0 Comments
Pin




Question Number 107706 by bemath last updated on 12/Aug/20
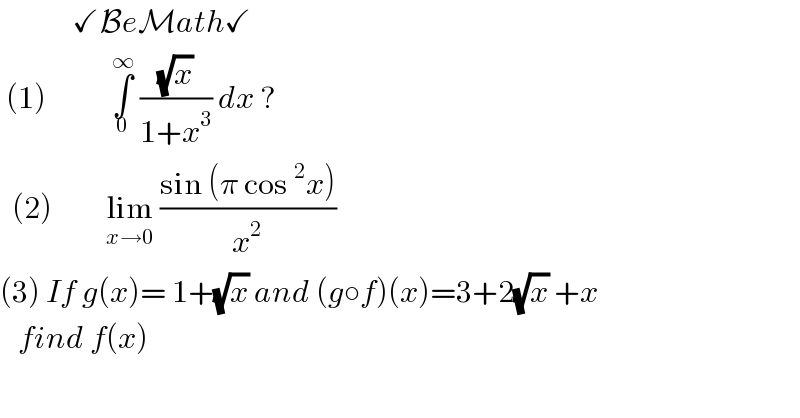
✓BeMath✓ (1) ∫_0 ^∞ ((√x)/(1+x^3 )) dx ? (2) lim_(x→0) ((sin (π cos^2 x))/x^2 ) (3) If g(x)= 1+(√x) and (g○f)(x)=3+2(√x) +x find f(x)
$$\:\:\:\:\:\:\:\:\:\:\:\:\checkmark\mathcal{B}{e}\mathcal{M}{ath}\checkmark \\ $$$$\:\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\sqrt{{x}}}{\mathrm{1}+{x}^{\mathrm{3}} }\:{dx}\:? \\ $$$$\:\:\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\pi\:\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }\: \\ $$$$\left(\mathrm{3}\right)\:{If}\:{g}\left({x}\right)=\:\mathrm{1}+\sqrt{{x}}\:{and}\:\left({g}\circ{f}\right)\left({x}\right)=\mathrm{3}+\mathrm{2}\sqrt{{x}}\:+{x} \\ $$$$\:\:\:{find}\:{f}\left({x}\right) \\ $$
Answered by bemath last updated on 12/Aug/20
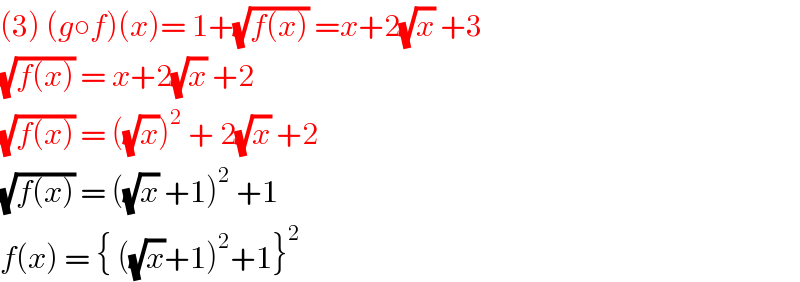
(3) (g○f)(x)= 1+(√(f(x))) =x+2(√x) +3 (√(f(x))) = x+2(√x) +2 (√(f(x))) = ((√x))^2 + 2(√x) +2 (√(f(x))) = ((√x) +1)^2 +1 f(x) = { ((√x)+1)^2 +1}^2
$$\left(\mathrm{3}\right)\:\left({g}\circ{f}\right)\left({x}\right)=\:\mathrm{1}+\sqrt{{f}\left({x}\right)}\:={x}+\mathrm{2}\sqrt{{x}}\:+\mathrm{3} \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:{x}+\mathrm{2}\sqrt{{x}}\:+\mathrm{2}\: \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:\left(\sqrt{{x}}\right)^{\mathrm{2}} \:+\:\mathrm{2}\sqrt{{x}}\:+\mathrm{2}\: \\ $$$$\sqrt{{f}\left({x}\right)}\:=\:\left(\sqrt{{x}}\:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}\: \\ $$$${f}\left({x}\right)\:=\:\left\{\:\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}^{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Aug/20
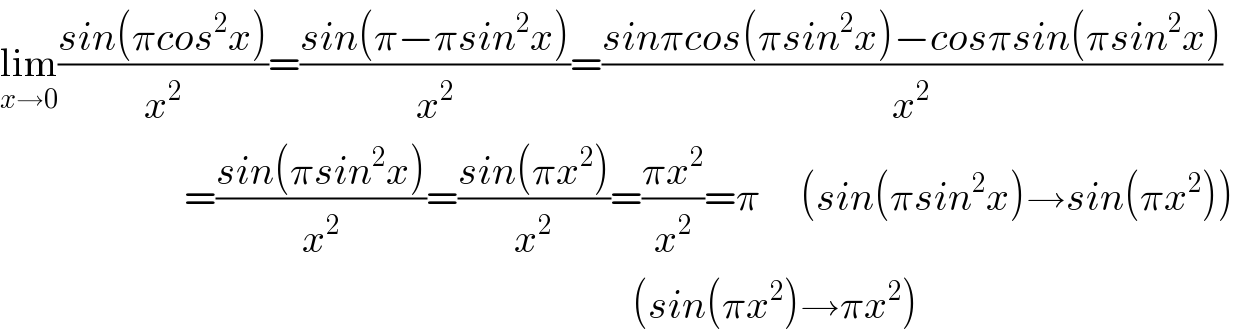
lim_(x→0) ((sin(πcos^2 x))/x^2 )=((sin(π−πsin^2 x))/x^2 )=((sinπcos(πsin^2 x)−cosπsin(πsin^2 x))/x^2 ) =((sin(πsin^2 x))/x^2 )=((sin(πx^2 ))/x^2 )=((πx^2 )/x^2 )=π (sin(πsin^2 x)→sin(πx^2 )) (sin(πx^2 )→πx^2 )
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\left(\pi−\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\pi{cos}\left(\pi{sin}^{\mathrm{2}} {x}\right)−{cos}\pi{sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\frac{{sin}\left(\pi{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }=\frac{\pi{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\pi\:\:\:\:\:\left({sin}\left(\pi{sin}^{\mathrm{2}} {x}\right)\rightarrow{sin}\left(\pi{x}^{\mathrm{2}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({sin}\left(\pi{x}^{\mathrm{2}} \right)\rightarrow\pi{x}^{\mathrm{2}} \right) \\ $$
Answered by Dwaipayan Shikari last updated on 12/Aug/20
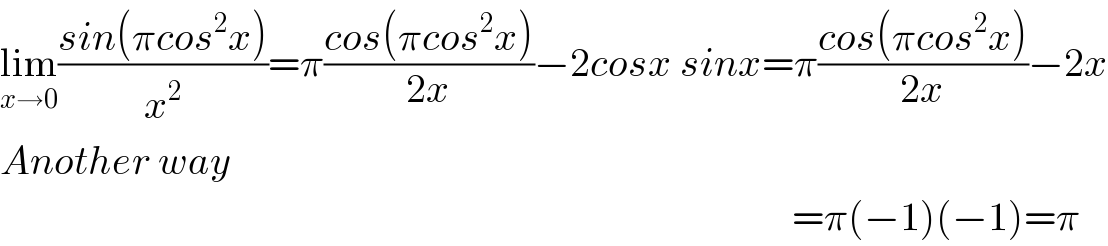
lim_(x→0) ((sin(πcos^2 x))/x^2 )=π((cos(πcos^2 x))/(2x))−2cosx sinx=π((cos(πcos^2 x))/(2x))−2x Another way =π(−1)(−1)=π
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }=\pi\frac{{cos}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\mathrm{2}{x}}−\mathrm{2}{cosx}\:{sinx}=\pi\frac{{cos}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\mathrm{2}{x}}−\mathrm{2}{x} \\ $$$${Another}\:{way} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)=\pi \\ $$
Answered by john santu last updated on 12/Aug/20
((♣JS♣)/…) (1) ∫ _0 ^∞ ((√x)/(1+x^3 )) dx [ let h=(√(x )) ] ∫_0 ^∞ (h/(1+h^6 )) .(2h)dh = ∫_0 ^∞ ((2h^2 )/(1+h^6 )) dh now set q=h^3 ; ∫_0 ^∞ (2/(1+q^3 )) .(1/3)dq = [(2/3) arc tan q ]_0 ^∞ = (2/3)×(π/2)= = (π/3)
$$\:\:\:\:\:\:\:\frac{\clubsuit\mathcal{JS}\clubsuit}{\ldots} \\ $$$$\left(\mathrm{1}\right)\:\int\overset{\infty} {\:}_{\mathrm{0}} \frac{\sqrt{{x}}}{\mathrm{1}+{x}^{\mathrm{3}} }\:{dx}\:\:\left[\:{let}\:{h}=\sqrt{{x}\:}\:\right] \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{h}}{\mathrm{1}+{h}^{\mathrm{6}} }\:.\left(\mathrm{2}{h}\right){dh}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}{h}^{\mathrm{2}} }{\mathrm{1}+{h}^{\mathrm{6}} }\:{dh} \\ $$$${now}\:{set}\:{q}={h}^{\mathrm{3}} ;\: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}}{\mathrm{1}+{q}^{\mathrm{3}} }\:.\frac{\mathrm{1}}{\mathrm{3}}{dq}\:=\:\left[\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arc}\:\mathrm{tan}\:{q}\:\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}=\:=\:\frac{\pi}{\mathrm{3}}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *