Menu Close

BeMath-1-1-tan-3-1-tan-4-1-tan-41-1-tan-42-2-f-x-g-h-x-h-x-2x-2-3x-If-f-1-14-then-g-5-

Tinku Tara 0 Comments
Pin




Question Number 107470 by bemath last updated on 11/Aug/20
↺BeMath↻ (1)(1+tan 3°)(1+tan 4°)(1+tan 41°)(1+tan 42°)=? (2)f(x)=g(h(x)); h(x)=2x^2 −3x. If f ′(−1)=14 then g ′(5)=?
$$\:\:\:\:\:\:\:\:\circlearrowleft\mathcal{B}{e}\mathcal{M}{ath}\circlearrowright \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{3}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{4}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{41}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{42}°\right)=? \\ $$$$\left(\mathrm{2}\right){f}\left({x}\right)={g}\left({h}\left({x}\right)\right);\:{h}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}. \\ $$$${If}\:{f}\:'\left(−\mathrm{1}\right)=\mathrm{14}\:{then}\:{g}\:'\left(\mathrm{5}\right)=? \\ $$
Answered by john santu last updated on 11/Aug/20
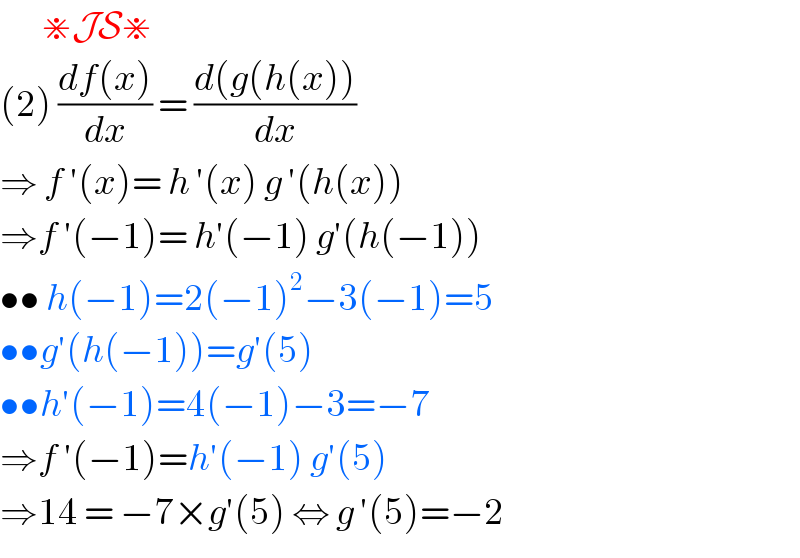
⋇JS⋇ (2) ((df(x))/dx) = ((d(g(h(x)))/dx) ⇒ f ′(x)= h ′(x) g ′(h(x)) ⇒f ′(−1)= h′(−1) g′(h(−1)) •• h(−1)=2(−1)^2 −3(−1)=5 ••g′(h(−1))=g′(5) ••h′(−1)=4(−1)−3=−7 ⇒f ′(−1)=h′(−1) g′(5) ⇒14 = −7×g′(5) ⇔ g ′(5)=−2
$$\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\left(\mathrm{2}\right)\:\frac{{df}\left({x}\right)}{{dx}}\:=\:\frac{{d}\left({g}\left({h}\left({x}\right)\right)\right.}{{dx}} \\ $$$$\Rightarrow\:{f}\:'\left({x}\right)=\:{h}\:'\left({x}\right)\:{g}\:'\left({h}\left({x}\right)\right) \\ $$$$\Rightarrow{f}\:'\left(−\mathrm{1}\right)=\:{h}'\left(−\mathrm{1}\right)\:{g}'\left({h}\left(−\mathrm{1}\right)\right) \\ $$$$\bullet\bullet\:{h}\left(−\mathrm{1}\right)=\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left(−\mathrm{1}\right)=\mathrm{5} \\ $$$$\bullet\bullet{g}'\left({h}\left(−\mathrm{1}\right)\right)={g}'\left(\mathrm{5}\right) \\ $$$$\bullet\bullet{h}'\left(−\mathrm{1}\right)=\mathrm{4}\left(−\mathrm{1}\right)−\mathrm{3}=−\mathrm{7} \\ $$$$\Rightarrow{f}\:'\left(−\mathrm{1}\right)={h}'\left(−\mathrm{1}\right)\:{g}'\left(\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{14}\:=\:−\mathrm{7}×{g}'\left(\mathrm{5}\right)\:\Leftrightarrow\:{g}\:'\left(\mathrm{5}\right)=−\mathrm{2} \\ $$
Answered by $@y@m last updated on 11/Aug/20
(1+tan 3)(1+tan 42)=1+tan 3+tan 42+tan 42tan 3 =1+(tan 45−tan 42tan 3)+tan 42tan 3 =2 ∴ the given expession =2×2 =4
$$\left(\mathrm{1}+\mathrm{tan}\:\mathrm{3}\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{42}\right)=\mathrm{1}+\mathrm{tan}\:\mathrm{3}+\mathrm{tan}\:\mathrm{42}+\mathrm{tan}\:\mathrm{42tan}\:\mathrm{3} \\ $$$$=\mathrm{1}+\left(\mathrm{tan}\:\mathrm{45}−\mathrm{tan}\:\mathrm{42tan}\:\mathrm{3}\right)+\mathrm{tan}\:\mathrm{42tan}\:\mathrm{3} \\ $$$$=\mathrm{2} \\ $$$$\therefore\:{the}\:{given}\:{expession} \\ $$$$=\mathrm{2}×\mathrm{2} \\ $$$$=\mathrm{4} \\ $$
Commented by bemath last updated on 11/Aug/20
thank you sir. but the question only (1+tan 3°)(1+tan 4°)(1+tan 42°)(1+tan 41°) so does mean the result 4 sir?
$${thank}\:{you}\:{sir}. \\ $$$${but}\:{the}\:{question}\:{only}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{3}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{4}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{42}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{41}°\right) \\ $$$${so}\:{does}\:{mean}\:{the}\:{result}\:\mathrm{4}\:{sir}? \\ $$
Commented by $@y@m last updated on 11/Aug/20
Oh. Yes.
$${Oh}. \\ $$$${Yes}. \\ $$
Answered by 1549442205PVT last updated on 12/Aug/20
We have :f ′(x)=g ′(h(x)).h′(x) f ′(−1)=g′(h(−1)).h′(−1)=14 ⇒g′(h(−1))=((14)/(−7))=−2⇔g′(5)=−2 b)1+tan42=tan87(1−tan42)=cot3(1−tan42) =((1−tan42)/(tan3))⇒tan3(1+tan42)=1−tan42 ⇒tan3=((1−tan42)/(1+tan42))⇒1+tan3=(2/(1+tan42)) 1+tan41=tan86(1−tan41)=cot4(1−tan41) ⇒1+tan4=(2/(1+tan41)) ⇒(1+tan3)(1+tan4)=(4/((1+tan41)(1+tan42))) ⇒(1+tan3)(1+tan4)(1+tan41)(1+tan42)=4
$$\mathrm{We}\:\mathrm{have}\::\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{g}\:'\left(\mathrm{h}\left(\mathrm{x}\right)\right).\mathrm{h}'\left(\mathrm{x}\right) \\ $$$$\mathrm{f}\:'\left(−\mathrm{1}\right)=\mathrm{g}'\left(\mathrm{h}\left(−\mathrm{1}\right)\right).\mathrm{h}'\left(−\mathrm{1}\right)=\mathrm{14} \\ $$$$\Rightarrow\mathrm{g}'\left(\mathrm{h}\left(−\mathrm{1}\right)\right)=\frac{\mathrm{14}}{−\mathrm{7}}=−\mathrm{2}\Leftrightarrow\mathrm{g}'\left(\mathrm{5}\right)=−\mathrm{2} \\ $$$$\left.\mathrm{b}\right)\mathrm{1}+\mathrm{tan42}=\mathrm{tan87}\left(\mathrm{1}−\mathrm{tan42}\right)=\mathrm{cot3}\left(\mathrm{1}−\mathrm{tan42}\right) \\ $$$$=\frac{\mathrm{1}−\mathrm{tan42}}{\mathrm{tan3}}\Rightarrow\mathrm{tan3}\left(\mathrm{1}+\mathrm{tan42}\right)=\mathrm{1}−\mathrm{tan42} \\ $$$$\Rightarrow\mathrm{tan3}=\frac{\mathrm{1}−\mathrm{tan42}}{\mathrm{1}+\mathrm{tan42}}\Rightarrow\mathrm{1}+\mathrm{tan3}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan42}} \\ $$$$\mathrm{1}+\mathrm{tan41}=\mathrm{tan86}\left(\mathrm{1}−\mathrm{tan41}\right)=\mathrm{cot4}\left(\mathrm{1}−\mathrm{tan41}\right) \\ $$$$\Rightarrow\mathrm{1}+\mathrm{tan4}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan41}} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{tan3}\right)\left(\mathrm{1}+\mathrm{tan4}\right)=\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{tan41}\right)\left(\mathrm{1}+\mathrm{tan42}\right)} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{tan3}\right)\left(\mathrm{1}+\mathrm{tan4}\right)\left(\mathrm{1}+\mathrm{tan41}\right)\left(\mathrm{1}+\mathrm{tan42}\right)=\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *