Question Number 106775 by bemath last updated on 07/Aug/20
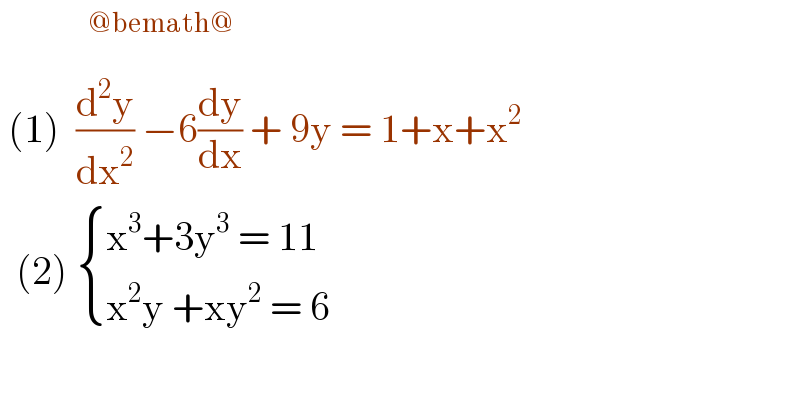
$$\:\:\:\:\:\:\:\:\:\:\:^{@\mathrm{bemath}@} \\ $$$$\:\left(\mathrm{1}\right)\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:−\mathrm{6}\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{9y}\:=\:\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \\ $$$$\:\:\left(\mathrm{2}\right)\:\begin{cases}{\mathrm{x}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{3}} \:=\:\mathrm{11}}\\{\mathrm{x}^{\mathrm{2}} \mathrm{y}\:+\mathrm{xy}^{\mathrm{2}} \:=\:\mathrm{6}}\end{cases}\: \\ $$
Answered by abdomathmax last updated on 07/Aug/20
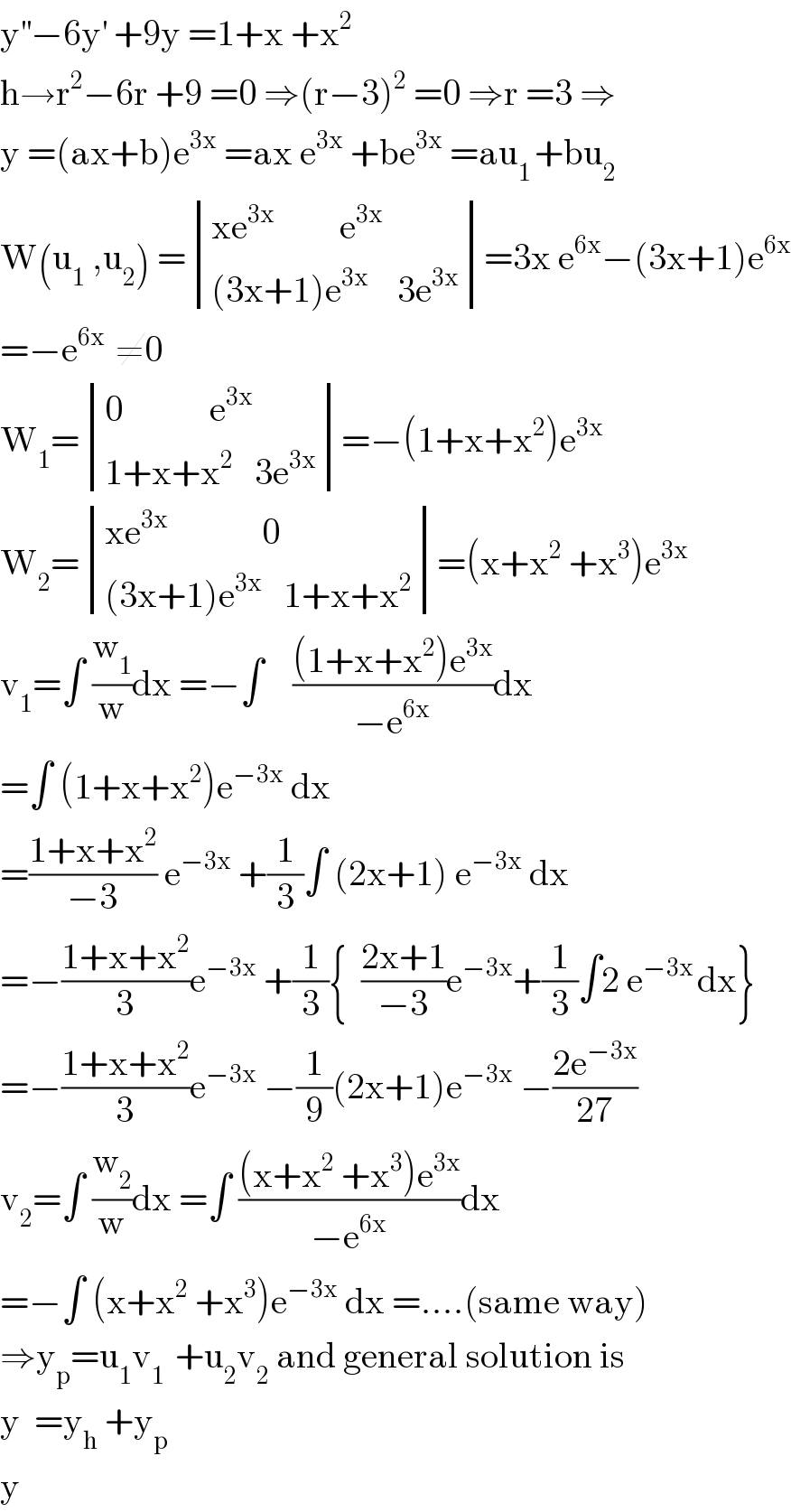
$$\mathrm{y}^{''} −\mathrm{6y}^{'} \:+\mathrm{9y}\:=\mathrm{1}+\mathrm{x}\:+\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{6r}\:+\mathrm{9}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{r}−\mathrm{3}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{r}\:=\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{y}\:=\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{e}^{\mathrm{3x}} \:=\mathrm{ax}\:\mathrm{e}^{\mathrm{3x}} \:+\mathrm{be}^{\mathrm{3x}} \:=\mathrm{au}_{\mathrm{1}\:} +\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{xe}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\left(\mathrm{3x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{3x}} \:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=\mathrm{3x}\:\mathrm{e}^{\mathrm{6x}} −\left(\mathrm{3x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{6x}} \\ $$$$=−\mathrm{e}^{\mathrm{6x}\:} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=−\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{xe}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{3x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{3x}} \:\:\:\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\end{vmatrix}=\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{3}} \right)\mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{e}^{\mathrm{3x}} }{−\mathrm{e}^{\mathrm{6x}} }\mathrm{dx} \\ $$$$=\int\:\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{e}^{−\mathrm{3x}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }{−\mathrm{3}}\:\mathrm{e}^{−\mathrm{3x}} \:+\frac{\mathrm{1}}{\mathrm{3}}\int\:\left(\mathrm{2x}+\mathrm{1}\right)\:\mathrm{e}^{−\mathrm{3x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\mathrm{e}^{−\mathrm{3x}} \:+\frac{\mathrm{1}}{\mathrm{3}}\left\{\:\:\frac{\mathrm{2x}+\mathrm{1}}{−\mathrm{3}}\mathrm{e}^{−\mathrm{3x}} +\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{2}\:\mathrm{e}^{−\mathrm{3x}\:} \mathrm{dx}\right\} \\ $$$$=−\frac{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\mathrm{e}^{−\mathrm{3x}} \:−\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{3x}} \:−\frac{\mathrm{2e}^{−\mathrm{3x}} }{\mathrm{27}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{3}} \right)\mathrm{e}^{\mathrm{3x}} }{−\mathrm{e}^{\mathrm{6x}} }\mathrm{dx} \\ $$$$=−\int\:\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{3}} \right)\mathrm{e}^{−\mathrm{3x}} \:\mathrm{dx}\:=….\left(\mathrm{same}\:\mathrm{way}\right) \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}\:} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$\mathrm{y} \\ $$
Answered by bobhans last updated on 07/Aug/20
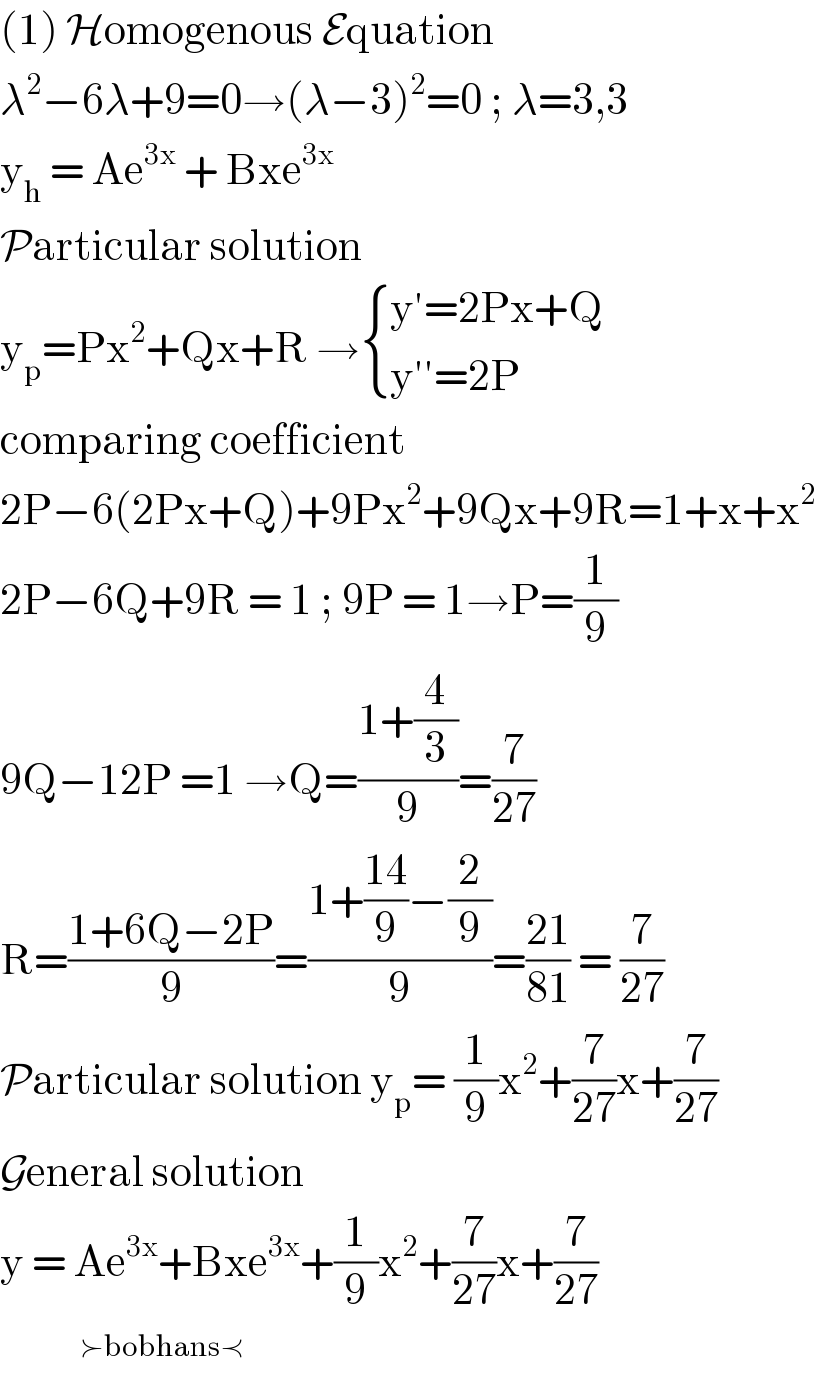
$$\left(\mathrm{1}\right)\:\mathcal{H}\mathrm{omogenous}\:\mathcal{E}\mathrm{quation}\: \\ $$$$\lambda^{\mathrm{2}} −\mathrm{6}\lambda+\mathrm{9}=\mathrm{0}\rightarrow\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0}\:;\:\lambda=\mathrm{3},\mathrm{3} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{\mathrm{3x}} \:+\:\mathrm{Bxe}^{\mathrm{3x}} \\ $$$$\mathcal{P}\mathrm{articular}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{Px}^{\mathrm{2}} +\mathrm{Qx}+\mathrm{R}\:\rightarrow\begin{cases}{\mathrm{y}'=\mathrm{2Px}+\mathrm{Q}}\\{\mathrm{y}''=\mathrm{2P}}\end{cases} \\ $$$$\mathrm{comparing}\:\mathrm{coefficient}\: \\ $$$$\mathrm{2P}−\mathrm{6}\left(\mathrm{2Px}+\mathrm{Q}\right)+\mathrm{9Px}^{\mathrm{2}} +\mathrm{9Qx}+\mathrm{9R}=\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{2P}−\mathrm{6Q}+\mathrm{9R}\:=\:\mathrm{1}\:;\:\mathrm{9P}\:=\:\mathrm{1}\rightarrow\mathrm{P}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{9Q}−\mathrm{12P}\:=\mathrm{1}\:\rightarrow\mathrm{Q}=\frac{\mathrm{1}+\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{9}}=\frac{\mathrm{7}}{\mathrm{27}} \\ $$$$\mathrm{R}=\frac{\mathrm{1}+\mathrm{6Q}−\mathrm{2P}}{\mathrm{9}}=\frac{\mathrm{1}+\frac{\mathrm{14}}{\mathrm{9}}−\frac{\mathrm{2}}{\mathrm{9}}}{\mathrm{9}}=\frac{\mathrm{21}}{\mathrm{81}}\:=\:\frac{\mathrm{7}}{\mathrm{27}} \\ $$$$\mathcal{P}\mathrm{articular}\:\mathrm{solution}\:\mathrm{y}_{\mathrm{p}} =\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{7}}{\mathrm{27}} \\ $$$$\mathcal{G}\mathrm{eneral}\:\mathrm{solution}\: \\ $$$$\mathrm{y}\:=\:\mathrm{Ae}^{\mathrm{3x}} +\mathrm{Bxe}^{\mathrm{3x}} +\frac{\mathrm{1}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{7}}{\mathrm{27}} \\ $$$$\:\:\:\:\:\:\:\:\:\:^{\succ\mathrm{bobhans}\prec\:} \\ $$
Answered by 1549442205PVT last updated on 07/Aug/20

$$\:\:\left(\mathrm{2}\right)\:\begin{cases}{\mathrm{x}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{3}} \:=\:\mathrm{11}\left(\mathrm{1}\right)}\\{\mathrm{x}^{\mathrm{2}} \mathrm{y}\:+\mathrm{xy}^{\mathrm{2}} \:=\:\mathrm{6}\left(\mathrm{2}\right)}\end{cases}\: \\ $$$$\mathrm{Multiplying}\:\mathrm{obliquely}\:\mathrm{two}\:\mathrm{equalities} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{6x}^{\mathrm{3}} +\mathrm{18y}^{\mathrm{3}} =\mathrm{11x}^{\mathrm{2}} \mathrm{y}+\mathrm{11xy}^{\mathrm{2}} \mathrm{and} \\ $$$$\mathrm{setting}\:\mathrm{y}=\mathrm{kx}\:\mathrm{we}\:\mathrm{obtain}: \\ $$$$\mathrm{6x}^{\mathrm{3}} +\mathrm{18k}^{\mathrm{3}} \mathrm{x}^{\mathrm{3}} =\mathrm{11kx}^{\mathrm{3}} +\mathrm{11k}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} .\mathrm{Dividing} \\ $$$$\mathrm{both}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{above}\:\mathrm{eqn}.\:\mathrm{by}\:\mathrm{x}^{\mathrm{3}} \neq\mathrm{0}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{18k}^{\mathrm{3}} −\mathrm{11k}^{\mathrm{2}} −\mathrm{11k}+\mathrm{6}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{2k}−\mathrm{1}\right)\left(\mathrm{9k}^{\mathrm{2}} −\mathrm{k}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\left.\mathrm{i}\right)\mathrm{2k}−\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{k}=\mathrm{1}/\mathrm{2}. \\ $$$$\mathrm{one}\:\mathrm{root}\Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\Leftrightarrow\mathrm{x}=\mathrm{2y}.\mathrm{Replace} \\ $$$$\mathrm{into}\:\mathrm{the}\:\mathrm{first}\:\mathrm{eqn}.\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{8y}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{3}} =\mathrm{11}\Leftrightarrow\mathrm{y}^{\mathrm{3}} =\mathrm{1}\Leftrightarrow\mathrm{y}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\left.\mathrm{ii}\right)\mathrm{9k}^{\mathrm{2}} −\mathrm{k}−\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{k}=\frac{\mathrm{1}\pm\sqrt{\mathrm{2017}}}{\mathrm{18}} \\ $$$$\left.\mathrm{a}\right)\mathrm{For}\:\mathrm{k}=\frac{\mathrm{1}+\sqrt{\mathrm{2017}}}{\mathrm{18}}\Rightarrow\mathrm{y}=\frac{\mathrm{1}+\sqrt{\mathrm{2017}}}{\mathrm{18}}\mathrm{x}. \\ $$$$\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\left(\mathrm{3k}^{\mathrm{3}} +\mathrm{1}\right)\mathrm{x}^{\mathrm{3}} =\mathrm{11} \\ $$$$\Leftrightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{11}}{\mathrm{3k}^{\mathrm{3}} +\mathrm{1}}}=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{21384}}{\mathrm{7996}+\mathrm{2020}\sqrt{\mathrm{2017}}}\:\:\:\:}\approx\mathrm{0}.\mathrm{600} \\ $$$$\mathrm{y}=\mathrm{kx}=\frac{\mathrm{1}+\sqrt{\mathrm{2017}}}{\mathrm{18}}×\:^{\mathrm{3}} \sqrt{\frac{\mathrm{21384}}{\mathrm{7996}+\mathrm{2020}\sqrt{\mathrm{2017}}}\:\:\:\:}\:\approx\mathrm{1}.\mathrm{5318} \\ $$$$\left.\mathrm{b}\right)\mathrm{For}\:\mathrm{k}=\frac{\mathrm{1}−\sqrt{\mathrm{2017}}}{\mathrm{18}}\Rightarrow\mathrm{y}=\frac{\mathrm{1}−\sqrt{\mathrm{2017}}}{\mathrm{18}}\mathrm{x} \\ $$$$\mathrm{Similarly},\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{11}}{\mathrm{3k}^{\mathrm{3}} +\mathrm{1}}}=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{21384}}{\mathrm{7996}−\mathrm{2020}\sqrt{\mathrm{2017}}}\:}\:\approx−\mathrm{06370} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{1}−\sqrt{\mathrm{2017}}}{\mathrm{18}}×\:^{\mathrm{3}} \sqrt{\frac{\mathrm{64512}}{\mathrm{23548}−\mathrm{2020}\sqrt{\mathrm{2017}}}\:}\:\approx\mathrm{1}.\mathrm{5540} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equtions} \\ $$$$\mathrm{has}\:\mathrm{three}\:\mathrm{solution}\::\left(\mathrm{x};\mathrm{y}\right)\in\left\{\left(\mathrm{2};\mathrm{1}\right);\right. \\ $$$$\left(\mathrm{0}.\mathrm{600};\mathrm{1}.\mathrm{5318}\right);\left(−\mathrm{0}.\mathrm{6370};\mathrm{1}.\mathrm{5540}\right) \\ $$
Commented by bemath last updated on 07/Aug/20

Commented by bemath last updated on 07/Aug/20
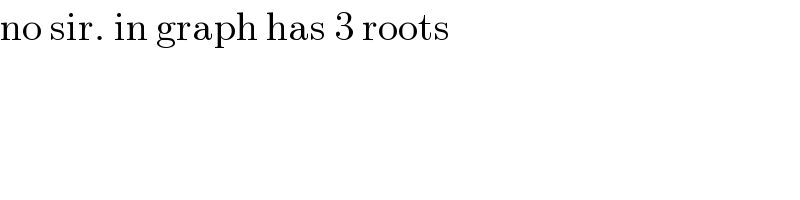
$$\mathrm{no}\:\mathrm{sir}.\:\mathrm{in}\:\mathrm{graph}\:\mathrm{has}\:\mathrm{3}\:\mathrm{roots}\: \\ $$
Commented by 1549442205PVT last updated on 07/Aug/20

$$\mathrm{Excuse},\mathrm{me}.\mathrm{I}\:\mathrm{mistaked}\:\mathrm{and}\:\mathrm{now}\:\mathrm{i}\:\mathrm{am} \\ $$$$\mathrm{correcting}\left(\mathrm{since}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\right. \\ $$$$\left.\mathrm{degree}\:\mathrm{3}\:\mathrm{w}.\mathrm{r}.\mathrm{t}.'\mathrm{k}'\:\mathrm{has}\:\mathrm{3}\:\mathrm{roots}\right) \\ $$
Commented by bemath last updated on 07/Aug/20

$$\mathrm{great}\:\mathrm{sir} \\ $$
