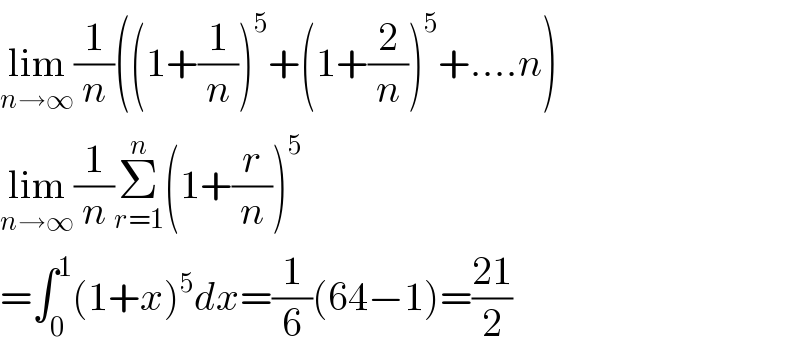Question Number 111313 by bemath last updated on 03/Sep/20
$$\:\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\left(\mathrm{1}\right)\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{5}} +\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{5}} +\left(\mathrm{n}+\mathrm{3}\right)^{\mathrm{5}} +…+\left(\mathrm{2n}\right)^{\mathrm{5}} }{\mathrm{n}^{\mathrm{6}} }? \\ $$$$\left(\mathrm{2}\right)\:\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx}\:\: \\ $$
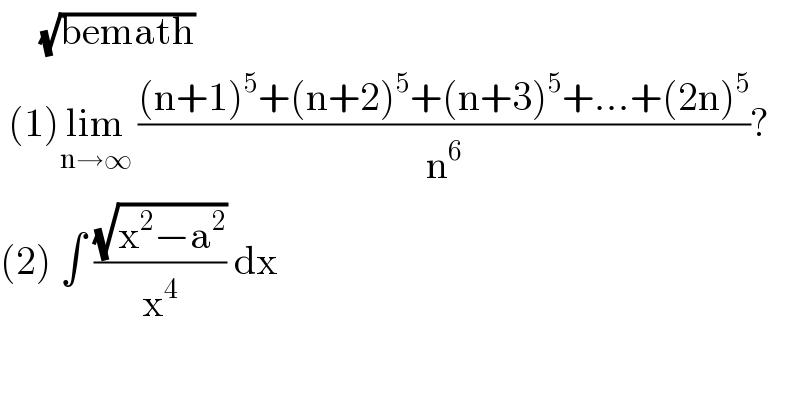
Answered by ajfour last updated on 03/Sep/20
$$\left(\mathrm{2}\right)\:\:\:\:{x}={a}\mathrm{sec}\:\theta\:\:\:\Rightarrow\:\:\mathrm{cos}\:\theta=\frac{{a}}{{x}} \\ $$$$\:\:\:\int\:\frac{{a}\mathrm{tan}\:\theta\left({a}\mathrm{sec}\:\theta\mathrm{tan}\:\theta\right){d}\theta}{{a}^{\mathrm{4}} \mathrm{sec}\:^{\mathrm{4}} \theta} \\ $$$$\:\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta{d}\theta\:\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left(\frac{\mathrm{sin}\:^{\mathrm{3}} \theta}{\mathrm{3}}\right)+{c} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\mathrm{3}/\mathrm{2}} +{c} \\ $$
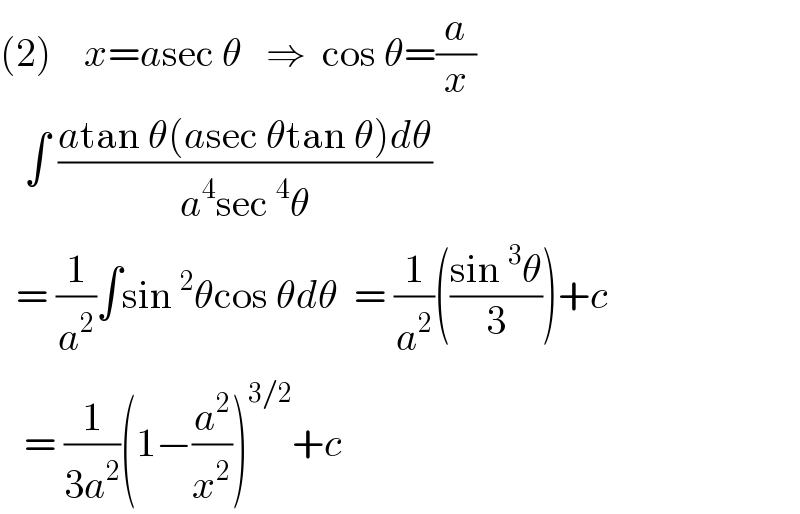
Commented by bemath last updated on 03/Sep/20
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by bobhans last updated on 03/Sep/20
![(■) I=∫ ((√(x^2 −a^2 ))/x^4 ) dx [ let x = a sec t ⇒ dx = asec t tan t dt ] I = ∫((√(a^2 (sec^2 t−1)))/(a^4 sec^4 t)). a sec t tan t dt I= (1/a^2 ) ∫ ((tan^2 t )/(sec^3 t)) dt = (1/a^2 )∫ sin^2 t cos t dt I = (1/a^2 ) ∫ sin^2 t d(sin t) = (1/(3a^2 )) sin^3 t + c I = (1/(3a^2 )) (((√(x^2 −a^2 ))/x))^3 + c = (1/(3a^2 x^3 ))(√((x^2 −a^2 )^3 )) + c](https://www.tinkutara.com/question/Q111316.png)
$$\left(\blacksquare\right)\:\mathrm{I}=\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx}\: \\ $$$$\:\:\left[\:\mathrm{let}\:\mathrm{x}\:=\:\mathrm{a}\:\mathrm{sec}\:\mathrm{t}\:\Rightarrow\:\mathrm{dx}\:=\:\mathrm{asec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt}\:\right]\: \\ $$$$\mathrm{I}\:=\:\int\frac{\sqrt{\mathrm{a}^{\mathrm{2}} \left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)}}{\mathrm{a}^{\mathrm{4}} \:\mathrm{sec}\:^{\mathrm{4}} \mathrm{t}}.\:\mathrm{a}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\:\int\:\frac{\mathrm{tan}^{\mathrm{2}} \:\mathrm{t}\:}{\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}}\:\mathrm{dt}\:=\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{cos}\:\mathrm{t}\:\mathrm{dt}\: \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\:\int\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{d}\left(\mathrm{sin}\:\mathrm{t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{t}\:+\:\mathrm{c} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\:\left(\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{x}}\right)^{\mathrm{3}} +\:\mathrm{c}\:=\:\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} }\sqrt{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{3}} }\:+\:\mathrm{c} \\ $$
Answered by bobhans last updated on 03/Sep/20
![(★) L = lim_(n→∞) [(1/n^6 ) Σ_(k=1) ^n (n+k)^5 ] L = lim_(n→∞) [ Σ_(k=1) ^n (1+(k/n))^5 .(1/n) ] recall ∫_a ^b f(x) dx = lim_(n→∞) Σ_(k=1) ^n f(x+k.△x).△x where △x = ((b−a)/n), we have △x = (1/n) by letting → { ((a=1)),((b=2)) :} therefore L = ∫_1 ^2 x^5 dx = [(1/6)x^6 ]_1 ^2 =((63)/6)=((21)/2)](https://www.tinkutara.com/question/Q111317.png)
$$\left(\bigstar\right)\:\mathrm{L}\:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{6}} }\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{n}+\mathrm{k}\right)^{\mathrm{5}} \:\right] \\ $$$$\:\:\:\mathrm{L}\:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{5}} .\frac{\mathrm{1}}{\mathrm{n}}\:\right] \\ $$$$\:\:\:\mathrm{recall}\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\mathrm{f}\left(\mathrm{x}+\mathrm{k}.\bigtriangleup\mathrm{x}\right).\bigtriangleup\mathrm{x} \\ $$$$\mathrm{where}\:\bigtriangleup\mathrm{x}\:=\:\frac{\mathrm{b}−\mathrm{a}}{\mathrm{n}},\:\mathrm{we}\:\mathrm{have}\:\bigtriangleup\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\mathrm{by}\:\mathrm{letting}\:\rightarrow\begin{cases}{\mathrm{a}=\mathrm{1}}\\{\mathrm{b}=\mathrm{2}}\end{cases} \\ $$$$\mathrm{therefore}\:\mathrm{L}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\mathrm{x}^{\mathrm{5}} \:\mathrm{dx}\:=\:\left[\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{6}} \:\right]_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{6}}=\frac{\mathrm{21}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 03/Sep/20
$$\mathrm{yes}…\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Sep/20
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\left(\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{5}} +\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)^{\mathrm{5}} +….{n}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{1}+\frac{{r}}{{n}}\right)^{\mathrm{5}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right)^{\mathrm{5}} {dx}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{64}−\mathrm{1}\right)=\frac{\mathrm{21}}{\mathrm{2}} \\ $$