Menu Close

bemath-1-lim-x-2x-2-x-3-1-3-x-2-lim-x-1-1-x-1-sin-pix-3-0-x-2-f-t-dt-x-cos-pix-Find-f-4-

Tinku Tara 0 Comments
Pin




Question Number 111498 by bemath last updated on 04/Sep/20
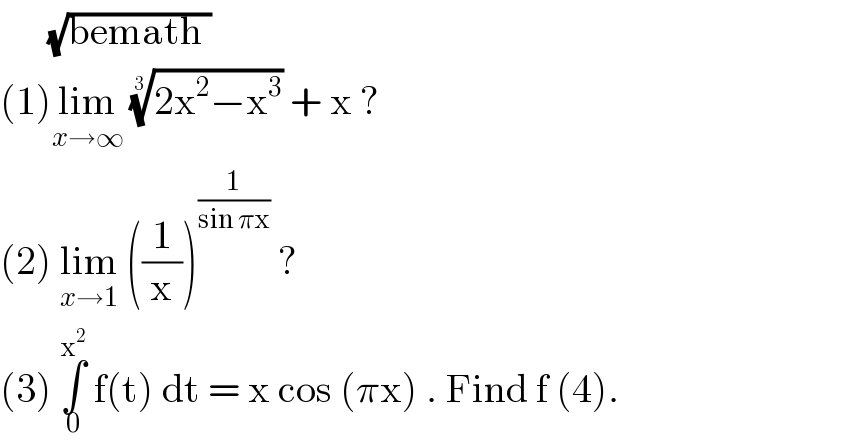
(√(bemath )) (1)lim_(x→∞) ((2x^2 −x^3 ))^(1/(3 )) + x ? (2) lim_(x→1) ((1/x))^(1/(sin πx)) ? (3) ∫_0 ^x^2 f(t) dt = x cos (πx) . Find f (4).
$$\:\:\:\:\:\:\sqrt{\mathrm{bemath}\:} \\ $$$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} }\:+\:\mathrm{x}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:\pi\mathrm{x}}} \:? \\ $$$$\left(\mathrm{3}\right)\:\underset{\mathrm{0}} {\overset{\mathrm{x}^{\mathrm{2}} } {\int}}\:\mathrm{f}\left(\mathrm{t}\right)\:\mathrm{dt}\:=\:\mathrm{x}\:\mathrm{cos}\:\left(\pi\mathrm{x}\right)\:.\:\mathrm{Find}\:\mathrm{f}\:\left(\mathrm{4}\right). \\ $$
Answered by john santu last updated on 04/Sep/20
let x = (1/t)→ { ((x→∞)),((t→0)) :} L=lim_(t→0) (((2/t^2 )−(1/t^3 )))^(1/(3 )) + (1/t) L= lim_(t→0) (((2t−1)/t^3 ))^(1/(3 )) + (1/t) L = lim_(t→0) ((((2t−1))^(1/(3 )) +1)/t) L= lim_(t→0) ((2t)/(t[ (2t−1)^2 −(2t−1)+1 ])) L= lim_(t→0) (2/((2t−1)^2 +2−2t)) = (2/3).
$$\:\:{let}\:{x}\:=\:\frac{\mathrm{1}}{{t}}\rightarrow\begin{cases}{{x}\rightarrow\infty}\\{{t}\rightarrow\mathrm{0}}\end{cases} \\ $$$${L}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{2}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }}\:+\:\frac{\mathrm{1}}{{t}} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{3}} }}\:+\:\frac{\mathrm{1}}{{t}} \\ $$$${L}\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{2}{t}−\mathrm{1}}+\mathrm{1}}{{t}} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{t}}{{t}\left[\:\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2}{t}−\mathrm{1}\right)+\mathrm{1}\:\right]} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}−\mathrm{2}{t}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}. \\ $$
Answered by bemath last updated on 04/Sep/20
Commented by bemath last updated on 04/Sep/20
typo in (x)^(1/(3 )) it should be (x^3 )^(1/(3 ))
$${typo}\:{in}\:\sqrt[{\mathrm{3}\:}]{{x}}\:{it}\:{should}\:{be}\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{3}} } \\ $$
Answered by john santu last updated on 04/Sep/20
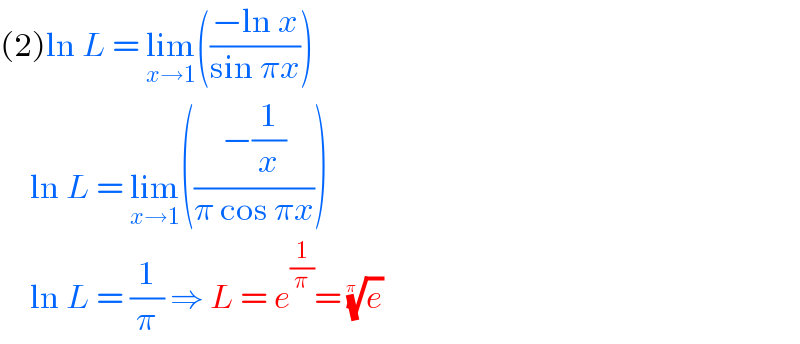
(2)ln L = lim_(x→1) (((−ln x)/(sin πx))) ln L = lim_(x→1) (((−(1/x))/(π cos πx))) ln L = (1/π) ⇒ L = e^(1/π) = (e)^(1/(π ))
$$\left(\mathrm{2}\right)\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{−\mathrm{ln}\:{x}}{\mathrm{sin}\:\pi{x}}\right) \\ $$$$\:\:\:\:\:\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{−\frac{\mathrm{1}}{{x}}}{\pi\:\mathrm{cos}\:\pi{x}}\right) \\ $$$$\:\:\:\:\:\mathrm{ln}\:{L}\:=\:\frac{\mathrm{1}}{\pi}\:\Rightarrow\:{L}\:=\:{e}^{\frac{\mathrm{1}}{\pi}} =\:\sqrt[{\pi\:}]{{e}}\: \\ $$
Answered by john santu last updated on 04/Sep/20
(3) (d/dx) [∫_0 ^( x^2 ) f(t) dt ] = (d/dx) [x cos πx ] ⇒ 2x f(x^2 ) = cos πx −πx sin πx put x = 2 ⇒ 4f(4) = cos 2π−2π sin 2π ⇒ f(4) = (1/4)
$$\left(\mathrm{3}\right)\:\frac{{d}}{{dx}}\:\left[\int_{\mathrm{0}} ^{\:\:{x}^{\mathrm{2}} } {f}\left({t}\right)\:{dt}\:\right]\:=\:\frac{{d}}{{dx}}\:\left[{x}\:\mathrm{cos}\:\pi{x}\:\right] \\ $$$$\Rightarrow\:\mathrm{2}{x}\:{f}\left({x}^{\mathrm{2}} \right)\:=\:\mathrm{cos}\:\pi{x}\:−\pi{x}\:\mathrm{sin}\:\pi{x} \\ $$$${put}\:{x}\:=\:\mathrm{2}\: \\ $$$$\Rightarrow\:\mathrm{4}{f}\left(\mathrm{4}\right)\:=\:\mathrm{cos}\:\mathrm{2}\pi−\mathrm{2}\pi\:\mathrm{sin}\:\mathrm{2}\pi \\ $$$$\Rightarrow\:{f}\left(\mathrm{4}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 04/Sep/20
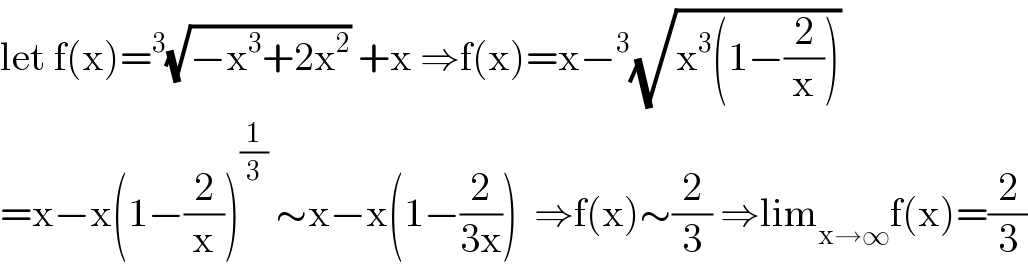
let f(x)=^3 (√(−x^3 +2x^2 )) +x ⇒f(x)=x−^3 (√(x^3 (1−(2/x)))) =x−x(1−(2/x))^(1/3) ∼x−x(1−(2/(3x))) ⇒f(x)∼(2/3) ⇒lim_(x→∞) f(x)=(2/3)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=^{\mathrm{3}} \sqrt{−\mathrm{x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} }\:+\mathrm{x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}−^{\mathrm{3}} \sqrt{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)} \\ $$$$=\mathrm{x}−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\sim\mathrm{x}−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3x}}\right)\:\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 04/Sep/20
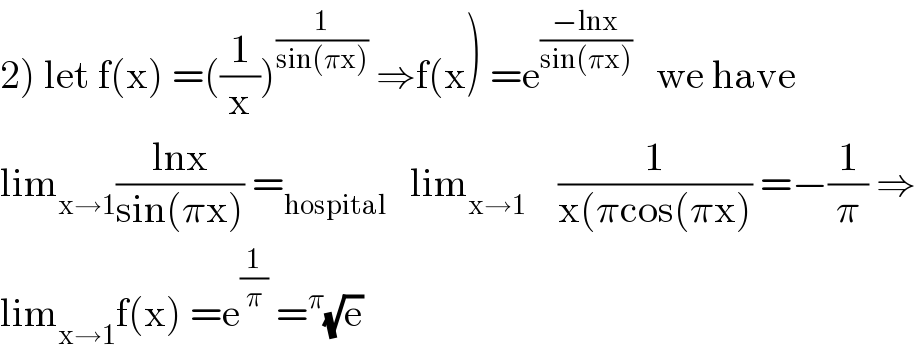
2) let f(x) =((1/x))^(1/(sin(πx))) ⇒f(x) =e^((−lnx)/(sin(πx))) we have lim_(x→1) ((lnx)/(sin(πx))) =_(hospital) lim_(x→1) (1/(x(πcos(πx))) =−(1/π) ⇒ lim_(x→1) f(x) =e^(1/π) =^π (√e)
$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{−\mathrm{lnx}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}} \:\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}\:=_{\mathrm{hospital}} \:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{x}\left(\pi\mathrm{cos}\left(\pi\mathrm{x}\right)\right.}\:=−\frac{\mathrm{1}}{\pi}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\pi}} \:=^{\pi} \sqrt{\mathrm{e}} \\ $$
Commented by bobhans last updated on 04/Sep/20
typo e^(−(1/π)) = (1/e^(1/π) )
$$\mathrm{typo}\:\mathrm{e}^{−\frac{\mathrm{1}}{\pi}} \:=\:\frac{\mathrm{1}}{\mathrm{e}^{\frac{\mathrm{1}}{\pi}} } \\ $$
Commented by mathmax by abdo last updated on 04/Sep/20
no typo!
$$\mathrm{no}\:\mathrm{typo}! \\ $$
Commented by bobhans last updated on 04/Sep/20
why ? you got e^(−(1/π)) ? it not same to (e)^(1/(π )) ???
$$\mathrm{why}\:?\:\:\mathrm{you}\:\mathrm{got}\:\mathrm{e}^{−\frac{\mathrm{1}}{\pi}} \:?\:\mathrm{it}\:\mathrm{not}\:\mathrm{same}\:\mathrm{to}\: \\ $$$$\sqrt[{\pi\:}]{\mathrm{e}}\:??? \\ $$
Answered by mathmax by abdo last updated on 04/Sep/20
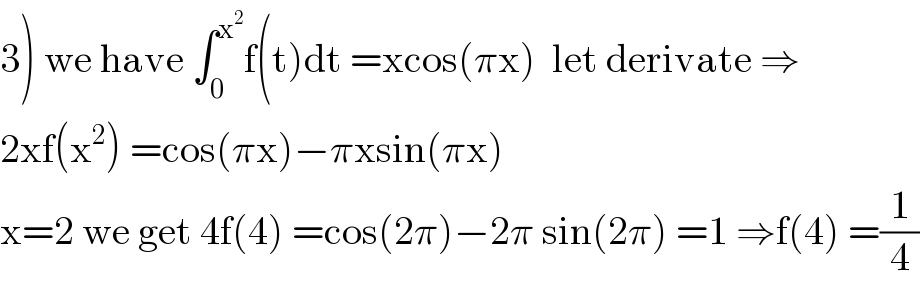
3) we have ∫_0 ^x^2 f(t)dt =xcos(πx) let derivate ⇒ 2xf(x^2 ) =cos(πx)−πxsin(πx) x=2 we get 4f(4) =cos(2π)−2π sin(2π) =1 ⇒f(4) =(1/4)
$$\left.\mathrm{3}\right)\:\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{xcos}\left(\pi\mathrm{x}\right)\:\:\mathrm{let}\:\mathrm{derivate}\:\Rightarrow \\ $$$$\mathrm{2xf}\left(\mathrm{x}^{\mathrm{2}} \right)\:=\mathrm{cos}\left(\pi\mathrm{x}\right)−\pi\mathrm{xsin}\left(\pi\mathrm{x}\right) \\ $$$$\mathrm{x}=\mathrm{2}\:\mathrm{we}\:\mathrm{get}\:\mathrm{4f}\left(\mathrm{4}\right)\:=\mathrm{cos}\left(\mathrm{2}\pi\right)−\mathrm{2}\pi\:\mathrm{sin}\left(\mathrm{2}\pi\right)\:=\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{4}\right)\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Sep/20
lim_(x→1) ((1/x))^(1/(sinπx)) =y (1/(sinπx))log((1/x))=logy (((1/x)−1)/(sinπx)) ((log(1+(1/x)−1))/(((1/x)−1)))=logy lim_(w→0) (((1/(w+1))−1)/(sin(πw+π)))=logy lim_(w→0) (((−w)/(w+1))/(−sinπw))=logy lim_(x→0) (((−w)/(w+1))/(−wπ))=logy (1/π)=logy y=e^(1/π)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{\frac{\mathrm{1}}{{sin}\pi{x}}} ={y} \\ $$$$\frac{\mathrm{1}}{{sin}\pi{x}}{log}\left(\frac{\mathrm{1}}{{x}}\right)={logy} \\ $$$$\frac{\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{sin}\pi{x}}\:\frac{{log}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}{\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}={logy} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{w}+\mathrm{1}}−\mathrm{1}}{{sin}\left(\pi{w}+\pi\right)}={logy} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−{w}}{{w}+\mathrm{1}}}{−{sin}\pi{w}}={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\:\frac{\frac{−{w}}{{w}+\mathrm{1}}}{−{w}\pi}={logy} \\ $$$$\frac{\mathrm{1}}{\pi}={logy} \\ $$$${y}={e}^{\frac{\mathrm{1}}{\pi}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *