Question Number 108095 by bemath last updated on 14/Aug/20
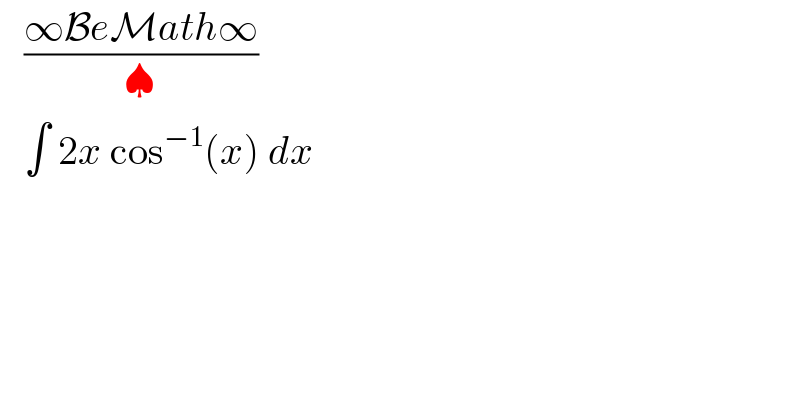
$$\:\:\:\frac{\infty\mathcal{B}{e}\mathcal{M}{ath}\infty}{\spadesuit} \\ $$$$\:\:\:\int\:\mathrm{2}{x}\:\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\:{dx}\: \\ $$
Answered by bemath last updated on 14/Aug/20

Answered by Dwaipayan Shikari last updated on 14/Aug/20
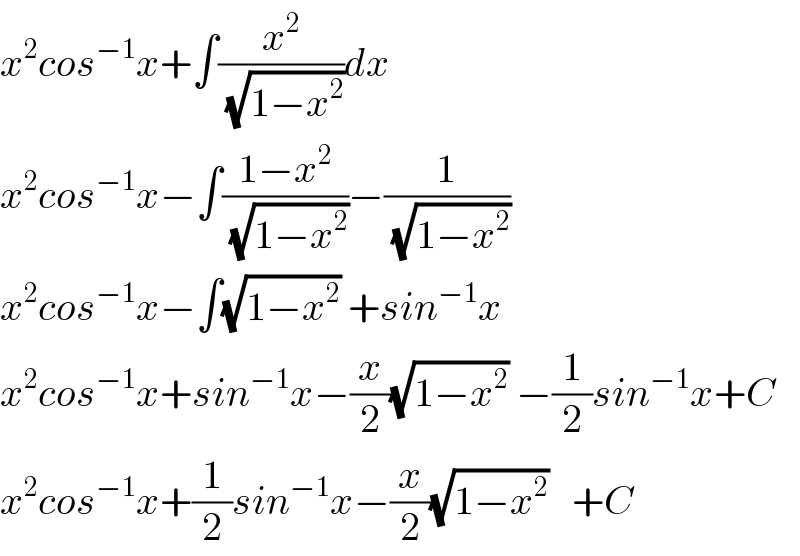
$${x}^{\mathrm{2}} {cos}^{−\mathrm{1}} {x}+\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${x}^{\mathrm{2}} {cos}^{−\mathrm{1}} {x}−\int\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${x}^{\mathrm{2}} {cos}^{−\mathrm{1}} {x}−\int\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+{sin}^{−\mathrm{1}} {x} \\ $$$${x}^{\mathrm{2}} {cos}^{−\mathrm{1}} {x}+{sin}^{−\mathrm{1}} {x}−\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} {x}+{C} \\ $$$${x}^{\mathrm{2}} {cos}^{−\mathrm{1}} {x}+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} {x}−\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\:+{C} \\ $$
Answered by mathmax by abdo last updated on 14/Aug/20

$$\mathrm{I}\:=\mathrm{2}\int\:\mathrm{x}\:\mathrm{arcosx}\:\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\left.\mathrm{I}\:=\mathrm{2}\left\{\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcosx}\:+\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right\}\:=\mathrm{x}^{\mathrm{2}} \mathrm{arcosx}+\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\right\}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:=_{\mathrm{x}=\mathrm{sint}} \:\:\:\int\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{cost}}\:\mathrm{cost}\:\mathrm{dt}\:=\int\:\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\int\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{t}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2t}\right)\:+\mathrm{C} \\ $$$$=\frac{\mathrm{t}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sint}\:\mathrm{cost}\:+\mathrm{C}\:\:=\frac{\mathrm{arcsinx}}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{x}^{\mathrm{2}} \:\mathrm{arcosx}\:+\frac{\mathrm{arcsinx}}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:+\mathrm{C} \\ $$
