Question Number 107714 by bemath last updated on 12/Aug/20
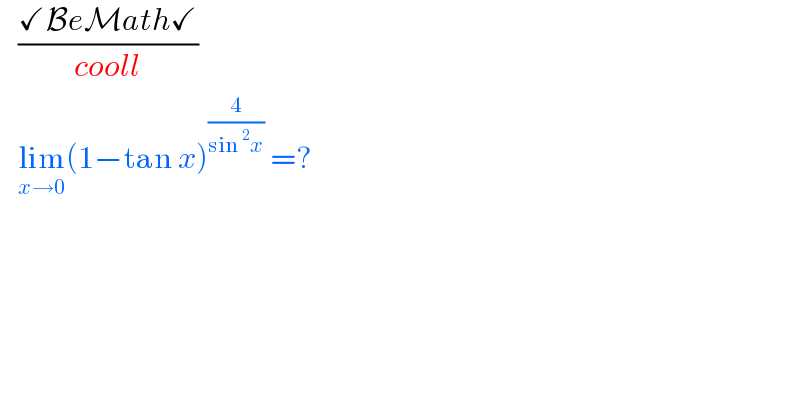
$$\:\:\:\frac{\checkmark\mathcal{B}{e}\mathcal{M}{ath}\checkmark}{{cooll}} \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\mathrm{tan}\:{x}\right)^{\frac{\mathrm{4}}{\mathrm{sin}\:^{\mathrm{2}} {x}}} \:=? \\ $$
Answered by bemath last updated on 12/Aug/20

Answered by Dwaipayan Shikari last updated on 12/Aug/20
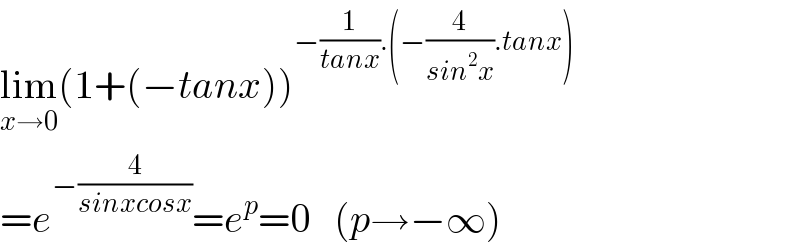
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(−{tanx}\right)\right)^{−\frac{\mathrm{1}}{{tanx}}.\left(−\frac{\mathrm{4}}{{sin}^{\mathrm{2}} {x}}.{tanx}\right)} \\ $$$$={e}^{−\frac{\mathrm{4}}{{sinxcosx}}} ={e}^{{p}} =\mathrm{0}\:\:\:\left({p}\rightarrow−\infty\right) \\ $$
