Question Number 111017 by bemath last updated on 01/Sep/20
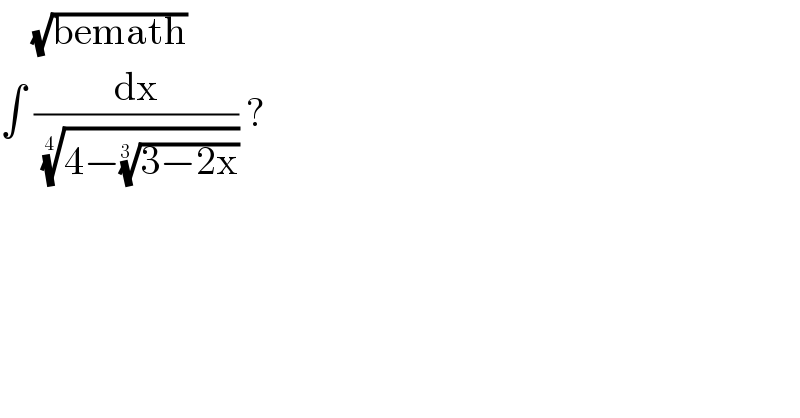
$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\int\:\frac{\mathrm{dx}}{\:\sqrt[{\mathrm{4}\:}]{\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2x}}}}\:? \\ $$
Answered by john santu last updated on 01/Sep/20
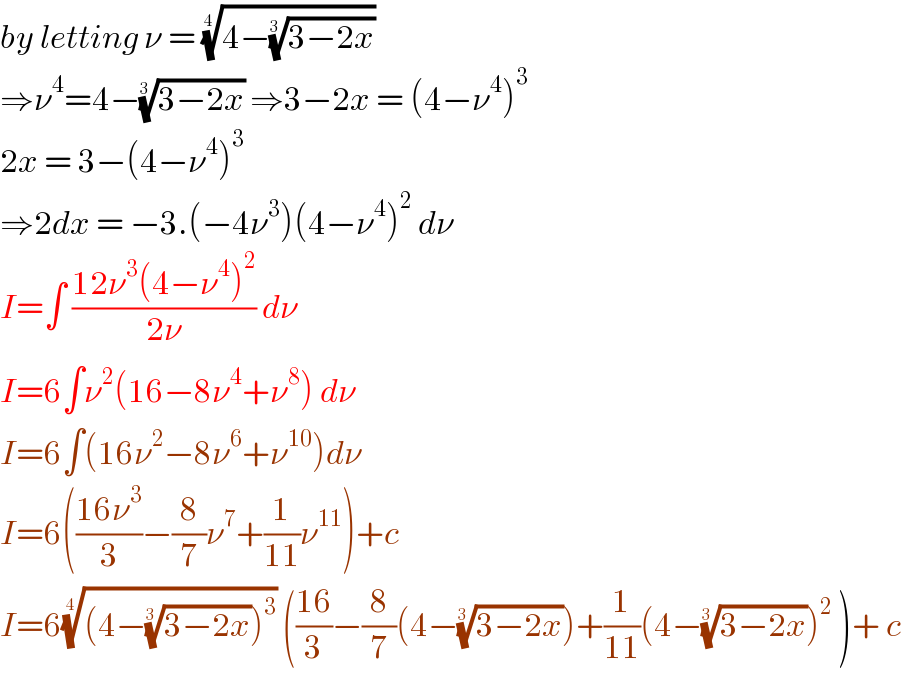
$${by}\:{letting}\:\nu\:=\:\sqrt[{\mathrm{4}\:}]{\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2}{x}}} \\ $$$$\Rightarrow\nu^{\mathrm{4}} =\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2}{x}}\:\Rightarrow\mathrm{3}−\mathrm{2}{x}\:=\:\left(\mathrm{4}−\nu^{\mathrm{4}} \right)^{\mathrm{3}} \\ $$$$\mathrm{2}{x}\:=\:\mathrm{3}−\left(\mathrm{4}−\nu^{\mathrm{4}} \right)^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{dx}\:=\:−\mathrm{3}.\left(−\mathrm{4}\nu^{\mathrm{3}} \right)\left(\mathrm{4}−\nu^{\mathrm{4}} \right)^{\mathrm{2}} \:{d}\nu \\ $$$${I}=\int\:\frac{\mathrm{12}\nu^{\mathrm{3}} \left(\mathrm{4}−\nu^{\mathrm{4}} \right)^{\mathrm{2}} }{\mathrm{2}\nu}\:{d}\nu \\ $$$${I}=\mathrm{6}\int\nu^{\mathrm{2}} \left(\mathrm{16}−\mathrm{8}\nu^{\mathrm{4}} +\nu^{\mathrm{8}} \right)\:{d}\nu \\ $$$${I}=\mathrm{6}\int\left(\mathrm{16}\nu^{\mathrm{2}} −\mathrm{8}\nu^{\mathrm{6}} +\nu^{\mathrm{10}} \right){d}\nu \\ $$$${I}=\mathrm{6}\left(\frac{\mathrm{16}\nu^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{7}}\nu^{\mathrm{7}} +\frac{\mathrm{1}}{\mathrm{11}}\nu^{\mathrm{11}} \right)+{c} \\ $$$${I}=\mathrm{6}\sqrt[{\mathrm{4}\:}]{\left(\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2}{x}}\right)^{\mathrm{3}} }\:\left(\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{7}}\left(\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2}{x}}\right)+\frac{\mathrm{1}}{\mathrm{11}}\left(\mathrm{4}−\sqrt[{\mathrm{3}\:}]{\mathrm{3}−\mathrm{2}{x}}\right)^{\mathrm{2}} \:\right)+\:{c}\: \\ $$
Answered by Dwaipayan Shikari last updated on 01/Sep/20
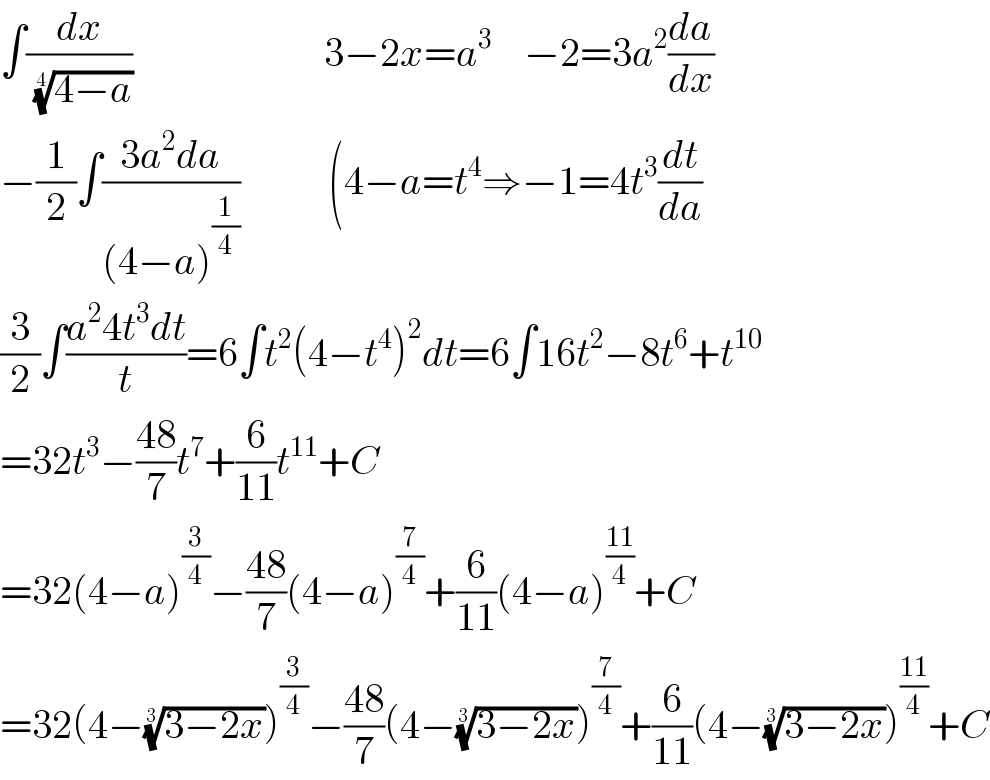
$$\int\frac{{dx}}{\:\sqrt[{\mathrm{4}}]{\mathrm{4}−{a}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−\mathrm{2}{x}={a}^{\mathrm{3}} \:\:\:\:−\mathrm{2}=\mathrm{3}{a}^{\mathrm{2}} \frac{{da}}{{dx}}\:\:\:\:\:\:\:\: \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{3}{a}^{\mathrm{2}} {da}}{\left(\mathrm{4}−{a}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{4}−{a}={t}^{\mathrm{4}} \Rightarrow−\mathrm{1}=\mathrm{4}{t}^{\mathrm{3}} \frac{{dt}}{{da}}\right. \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{a}^{\mathrm{2}} \mathrm{4}{t}^{\mathrm{3}} {dt}}{{t}}=\mathrm{6}\int{t}^{\mathrm{2}} \left(\mathrm{4}−{t}^{\mathrm{4}} \right)^{\mathrm{2}} {dt}=\mathrm{6}\int\mathrm{16}{t}^{\mathrm{2}} −\mathrm{8}{t}^{\mathrm{6}} +{t}^{\mathrm{10}} \\ $$$$=\mathrm{32}{t}^{\mathrm{3}} −\frac{\mathrm{48}}{\mathrm{7}}{t}^{\mathrm{7}} +\frac{\mathrm{6}}{\mathrm{11}}{t}^{\mathrm{11}} +{C} \\ $$$$=\mathrm{32}\left(\mathrm{4}−{a}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} −\frac{\mathrm{48}}{\mathrm{7}}\left(\mathrm{4}−{a}\right)^{\frac{\mathrm{7}}{\mathrm{4}}} +\frac{\mathrm{6}}{\mathrm{11}}\left(\mathrm{4}−{a}\right)^{\frac{\mathrm{11}}{\mathrm{4}}} +{C} \\ $$$$=\mathrm{32}\left(\mathrm{4}−\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{2}{x}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} −\frac{\mathrm{48}}{\mathrm{7}}\left(\mathrm{4}−\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{2}{x}}\right)^{\frac{\mathrm{7}}{\mathrm{4}}} +\frac{\mathrm{6}}{\mathrm{11}}\left(\mathrm{4}−\sqrt[{\mathrm{3}}]{\mathrm{3}−\mathrm{2}{x}}\right)^{\frac{\mathrm{11}}{\mathrm{4}}} +{C} \\ $$
