Menu Close

bemath-dx-x-1-1-3-x-1-2-1-3-

Tinku Tara 0 Comments
Pin




Question Number 111195 by bemath last updated on 02/Sep/20
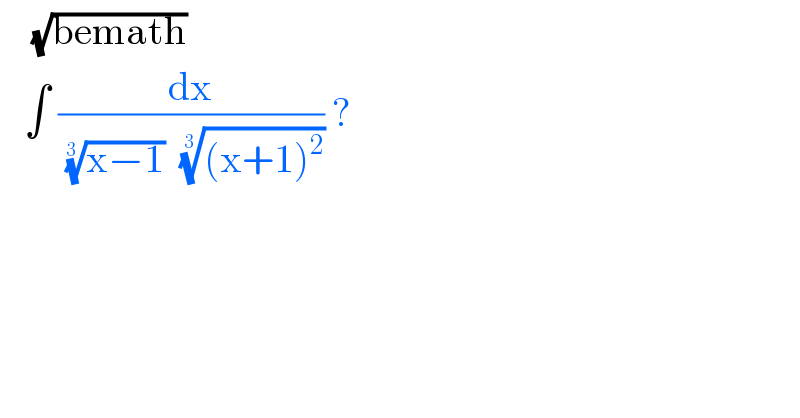
(√(bemath)) ∫ (dx/( ((x−1))^(1/(3 )) (((x+1)^2 ))^(1/(3 )) )) ?
$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\:\:\int\:\frac{\mathrm{dx}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:? \\ $$
Answered by Sarah85 last updated on 02/Sep/20
substitute t=(((x−1)/(x+1)))^(1/3) ⇔ x=−((t^3 +1)/(t^3 −1)) ⇒ ⇒ dx=(3/2)(((x−1)^2 (x+2)^4 ))^(1/3) dt ⇒ −3∫(t/(t^3 −1))dt=−∫(dt/(t−1))+∫((t−1)/(t^2 +t+1))dt= =−ln (t−1) +(1/2)ln (t^2 +t+1) −(√3)arctan ((2t+1)/( (√3))) = =(1/2)ln ((t^2 +t+1)/((t−1)^2 )) −(√3)arctan ((2t+1)/( (√3))) ...
$$\mathrm{substitute}\:{t}=\sqrt[{\mathrm{3}}]{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}\:\Leftrightarrow\:{x}=−\frac{{t}^{\mathrm{3}} +\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:{dx}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)^{\mathrm{4}} }{dt} \\ $$$$\Rightarrow \\ $$$$−\mathrm{3}\int\frac{{t}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}=−\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=−\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$… \\ $$
Commented by bemath last updated on 03/Sep/20
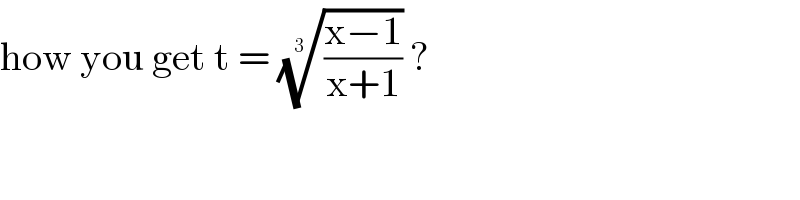
how you get t = (((x−1)/(x+1)))^(1/(3 )) ?
$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{t}\:=\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\:? \\ $$
Commented by Sarah85 last updated on 03/Sep/20
try and error
$$\mathrm{try}\:\mathrm{and}\:\mathrm{error} \\ $$
Answered by mindispower last updated on 02/Sep/20
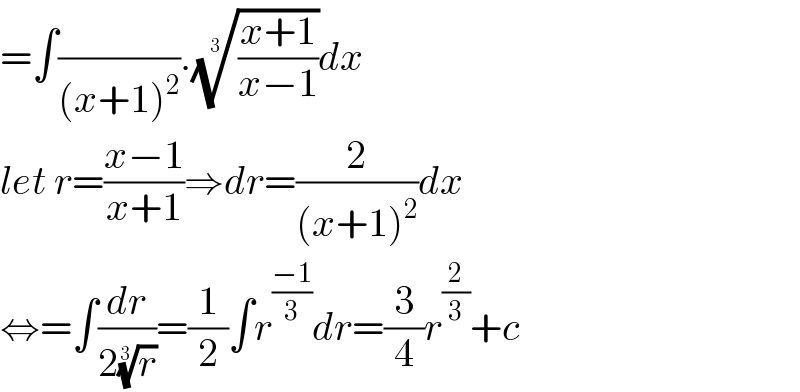
=∫(/((x+1)^2 )).(((x+1)/(x−1)))^(1/3) dx let r=((x−1)/(x+1))⇒dr=(2/((x+1)^2 ))dx ⇔=∫(dr/(2(r)^(1/3) ))=(1/2)∫r^((−1)/3) dr=(3/4)r^(2/3) +c
$$=\int\frac{}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }.\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}{dx} \\ $$$${let}\:{r}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\Rightarrow{dr}=\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\Leftrightarrow=\int\frac{{dr}}{\mathrm{2}\sqrt[{\mathrm{3}}]{{r}}}=\frac{\mathrm{1}}{\mathrm{2}}\int{r}^{\frac{−\mathrm{1}}{\mathrm{3}}} {dr}=\frac{\mathrm{3}}{\mathrm{4}}{r}^{\frac{\mathrm{2}}{\mathrm{3}}} +{c} \\ $$
Commented by Her_Majesty last updated on 02/Sep/20
something went wrong I think
$${something}\:{went}\:{wrong}\:{I}\:{think} \\ $$
Commented by bobhans last updated on 03/Sep/20
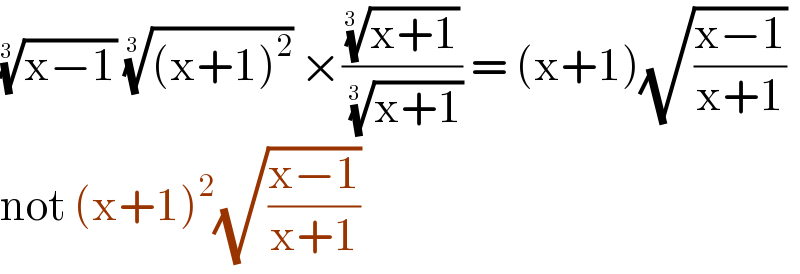
((x−1))^(1/(3 )) (((x+1)^2 ))^(1/(3 )) ×(((x+1))^(1/(3 )) /( ((x+1))^(1/(3 )) )) = (x+1)(√((x−1)/(x+1))) not (x+1)^2 (√((x−1)/(x+1)))
$$\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:×\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}\:=\:\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$$$\mathrm{not}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *