Question Number 106950 by bemath last updated on 08/Aug/20
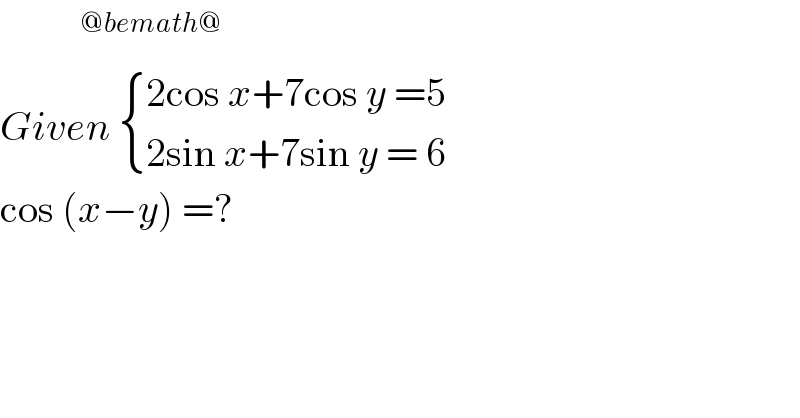
$$\:\:\:\:\:\:\:\:\:\:^{@{bemath}@} \\ $$$${Given}\:\begin{cases}{\mathrm{2cos}\:{x}+\mathrm{7cos}\:{y}\:=\mathrm{5}}\\{\mathrm{2sin}\:{x}+\mathrm{7sin}\:{y}\:=\:\mathrm{6}}\end{cases} \\ $$$$\mathrm{cos}\:\left({x}−{y}\right)\:=?\: \\ $$
Answered by john santu last updated on 08/Aug/20
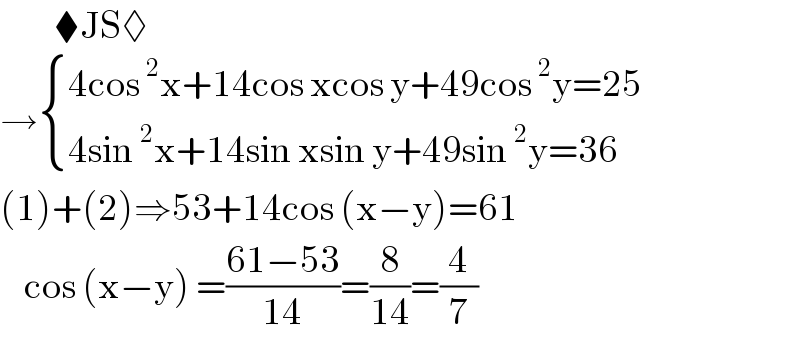
$$\:\:\:\:\:\:\:\:\:\blacklozenge\mathrm{JS}\lozenge \\ $$$$\rightarrow\begin{cases}{\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{14cos}\:\mathrm{xcos}\:\mathrm{y}+\mathrm{49cos}\:^{\mathrm{2}} \mathrm{y}=\mathrm{25}}\\{\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{14sin}\:\mathrm{xsin}\:\mathrm{y}+\mathrm{49sin}\:^{\mathrm{2}} \mathrm{y}=\mathrm{36}}\end{cases} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow\mathrm{53}+\mathrm{14cos}\:\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{61} \\ $$$$\:\:\:\:\mathrm{cos}\:\left(\mathrm{x}−\mathrm{y}\right)\:=\frac{\mathrm{61}−\mathrm{53}}{\mathrm{14}}=\frac{\mathrm{8}}{\mathrm{14}}=\frac{\mathrm{4}}{\mathrm{7}} \\ $$
