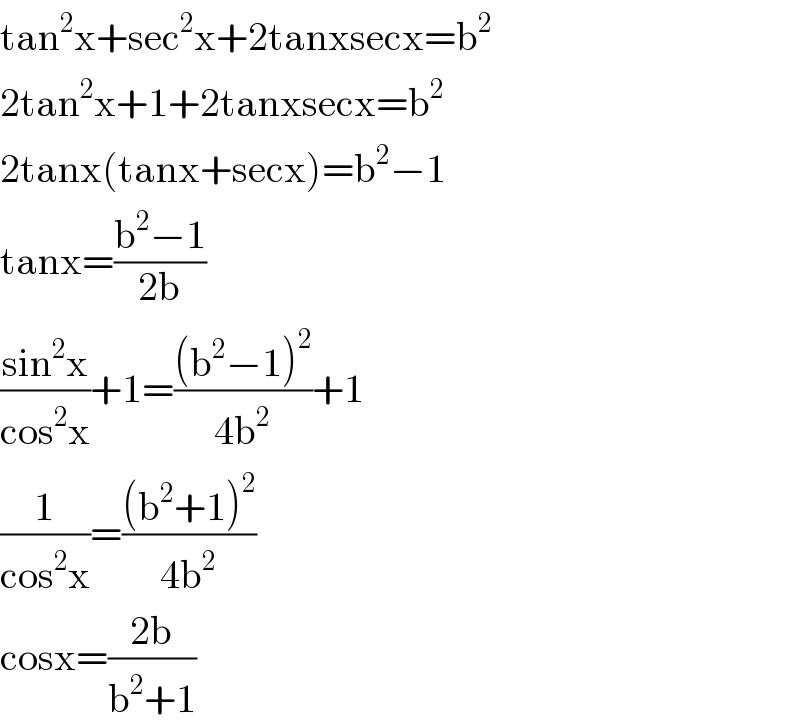Question Number 107364 by bemath last updated on 10/Aug/20
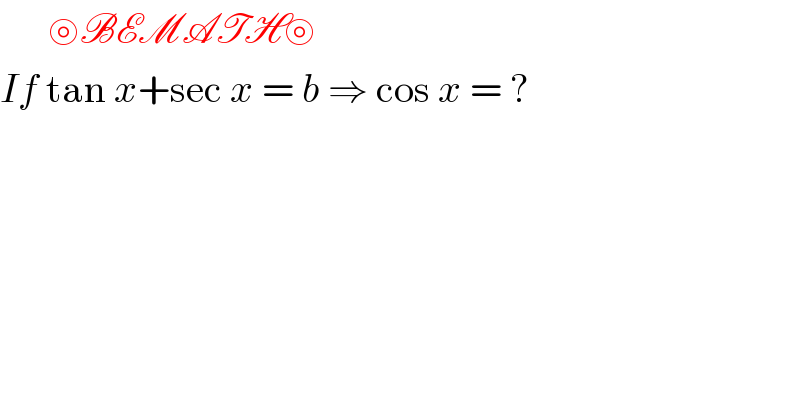
Answered by bobhans last updated on 10/Aug/20
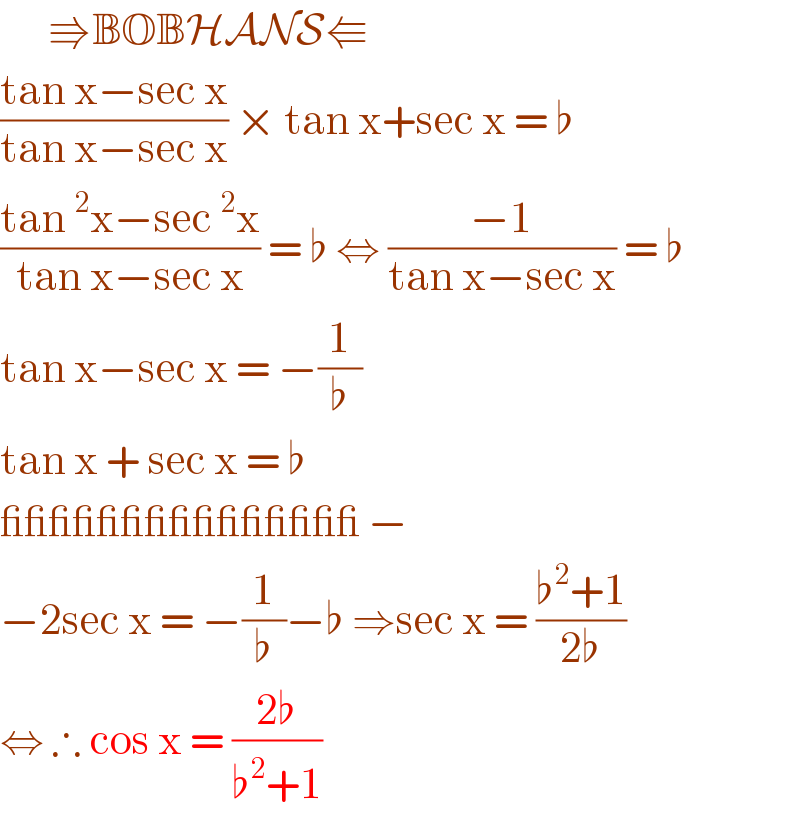
Answered by som(math1967) last updated on 10/Aug/20
![sec^2 x−tan^2 x=1 ⇒secx−tanx=(1/b) [∵secx+tanx=b] ∴2secx=b+(1/b) secx=((b^2 +1)/(2b)) ∴cosx=((2b)/(b^2 +1)) ans](https://www.tinkutara.com/question/Q107366.png)
Answered by Dwaipayan Shikari last updated on 10/Aug/20
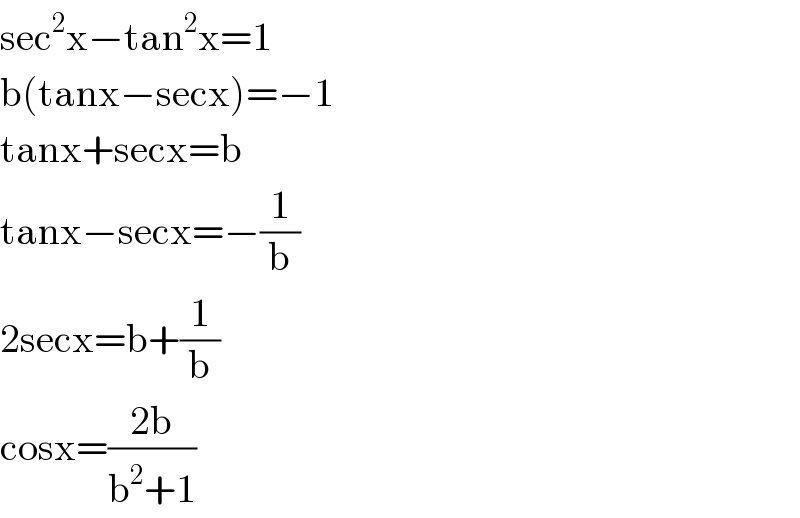
Answered by Dwaipayan Shikari last updated on 10/Aug/20