Question Number 111326 by bemath last updated on 03/Sep/20
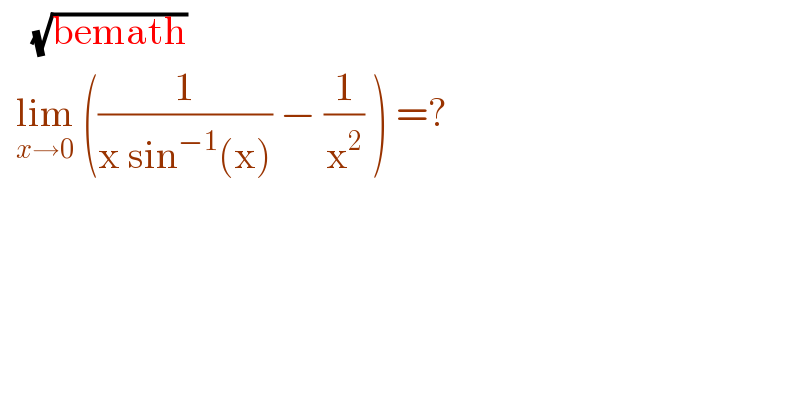
$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{x}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)}\:−\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\right)\:=? \\ $$
Answered by john santu last updated on 03/Sep/20
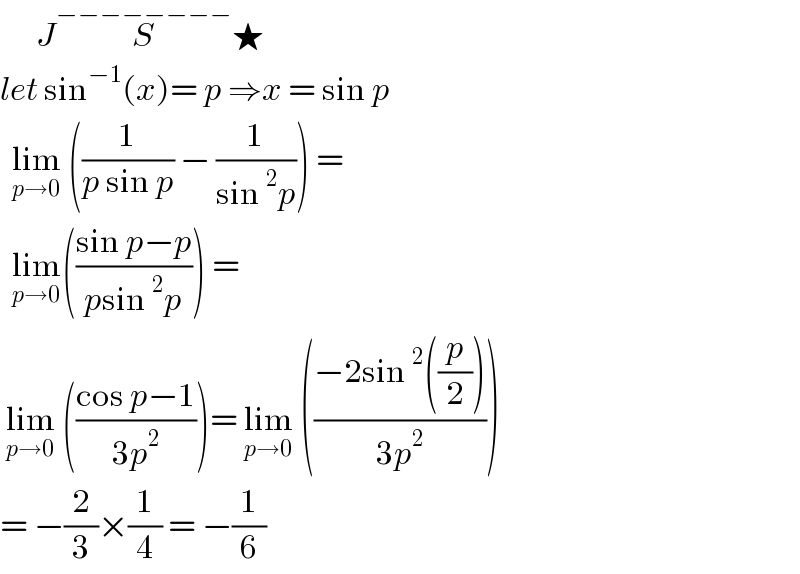
$$\:\:\:\:\:\:{J}\overset{−−−−−−−−} {{S}}\bigstar \\ $$$${let}\:\mathrm{sin}^{−\mathrm{1}} \left({x}\right)=\:{p}\:\Rightarrow{x}\:=\:\mathrm{sin}\:{p} \\ $$$$\:\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{p}\:\mathrm{sin}\:{p}}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {p}}\right)\:=\: \\ $$$$\:\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{p}−{p}}{{p}\mathrm{sin}\:^{\mathrm{2}} {p}}\right)\:= \\ $$$$\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{cos}\:{p}−\mathrm{1}}{\mathrm{3}{p}^{\mathrm{2}} }\right)=\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{p}}{\mathrm{2}}\right)}{\mathrm{3}{p}^{\mathrm{2}} }\right)\: \\ $$$$=\:−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}\:=\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by bemath last updated on 03/Sep/20

Answered by Dwaipayan Shikari last updated on 03/Sep/20
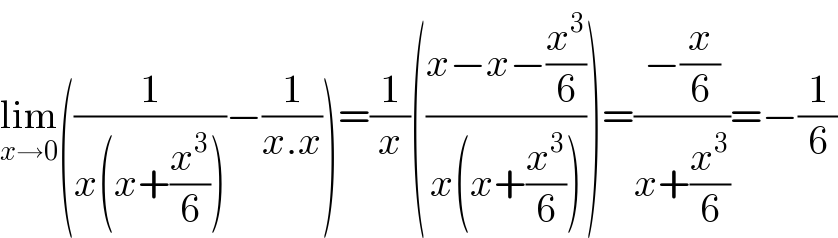
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}−\frac{\mathrm{1}}{{x}.{x}}\right)=\frac{\mathrm{1}}{{x}}\left(\frac{{x}−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}\right)=\frac{−\frac{{x}}{\mathrm{6}}}{{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
