Question Number 107414 by bemath last updated on 10/Aug/20
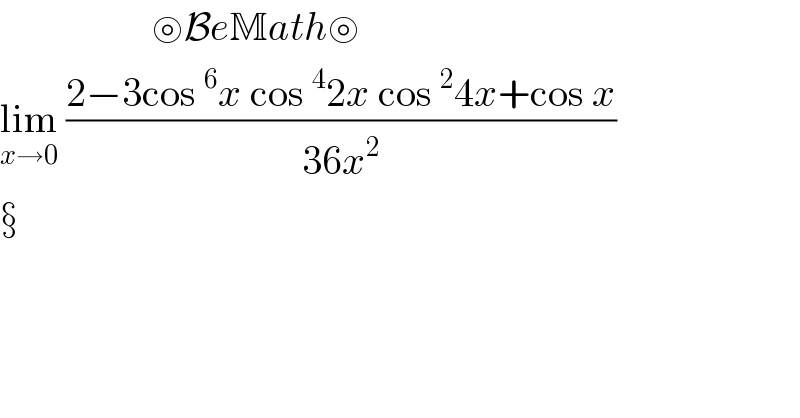
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\circledcirc\mathcal{B}{e}\mathbb{M}{ath}\circledcirc \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{3cos}\:^{\mathrm{6}} {x}\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{4}{x}+\mathrm{cos}\:{x}}{\mathrm{36}{x}^{\mathrm{2}} }\:\:\: \\ $$$$ \\ $$
Answered by ajfour last updated on 10/Aug/20
^2 }+(√(1−h^2 )))/(36h^2 )) =lim_(h^2 =k→0) ((2−3{1−3k){1−8k(1−k){1−16k+...}+(√(1−k)))/(36k)) = lim_(k→0) ((2−3(1−3k)(1−8k+..)(1−16k+..)+(√(1−k)))/(36k)) = lim_(k→0) ((2−3(1−27k+...)+1−(k/2))/(36k)) = ((81−(1/2))/(36)) = ((161)/(72)) .](https://www.tinkutara.com/question/Q107418.png)
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{4}{x}\right)+\mathrm{cos}\:{x}}{\mathrm{36}{x}^{\mathrm{2}} } \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\mathrm{3sin}\:^{\mathrm{2}} {x}\right)\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}\right)\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{4}{x}\right)+\mathrm{cos}\:{x}}{\mathrm{36}{x}^{\mathrm{2}} } \\ $$$$\:\:=\:\underset{\mathrm{sin}\:{x}={h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\mathrm{3}{h}^{\mathrm{2}} \right)\left\{\mathrm{1}−\mathrm{8}{h}^{\mathrm{2}} \left(\mathrm{1}−{h}^{\mathrm{2}} \right)\right\}\left\{\mathrm{1}−\mathrm{4}\left[\mathrm{4}\left({h}^{\mathrm{2}} \right)\left(\mathrm{1}−{h}^{\mathrm{2}} \right)\right]\left(\mathrm{1}−\mathrm{2}{h}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}+\sqrt{\mathrm{1}−{h}^{\mathrm{2}} }}{\mathrm{36}{h}^{\mathrm{2}} } \\ $$$$\:\:=\underset{{h}^{\mathrm{2}} ={k}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left\{\mathrm{1}−\mathrm{3}{k}\right)\left\{\mathrm{1}−\mathrm{8}{k}\left(\mathrm{1}−{k}\right)\left\{\mathrm{1}−\mathrm{16}{k}+…\right\}+\sqrt{\mathrm{1}−{k}}\right.}{\mathrm{36}{k}} \\ $$$$\:\:=\:\underset{{k}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\mathrm{3}{k}\right)\left(\mathrm{1}−\mathrm{8}{k}+..\right)\left(\mathrm{1}−\mathrm{16}{k}+..\right)+\sqrt{\mathrm{1}−{k}}}{\mathrm{36}{k}} \\ $$$$\:\:=\:\underset{{k}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\mathrm{27}{k}+…\right)+\mathrm{1}−\frac{{k}}{\mathrm{2}}}{\mathrm{36}{k}} \\ $$$$\:\:=\:\frac{\mathrm{81}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{36}}\:=\:\frac{\mathrm{161}}{\mathrm{72}}\:. \\ $$
Answered by john santu last updated on 11/Aug/20
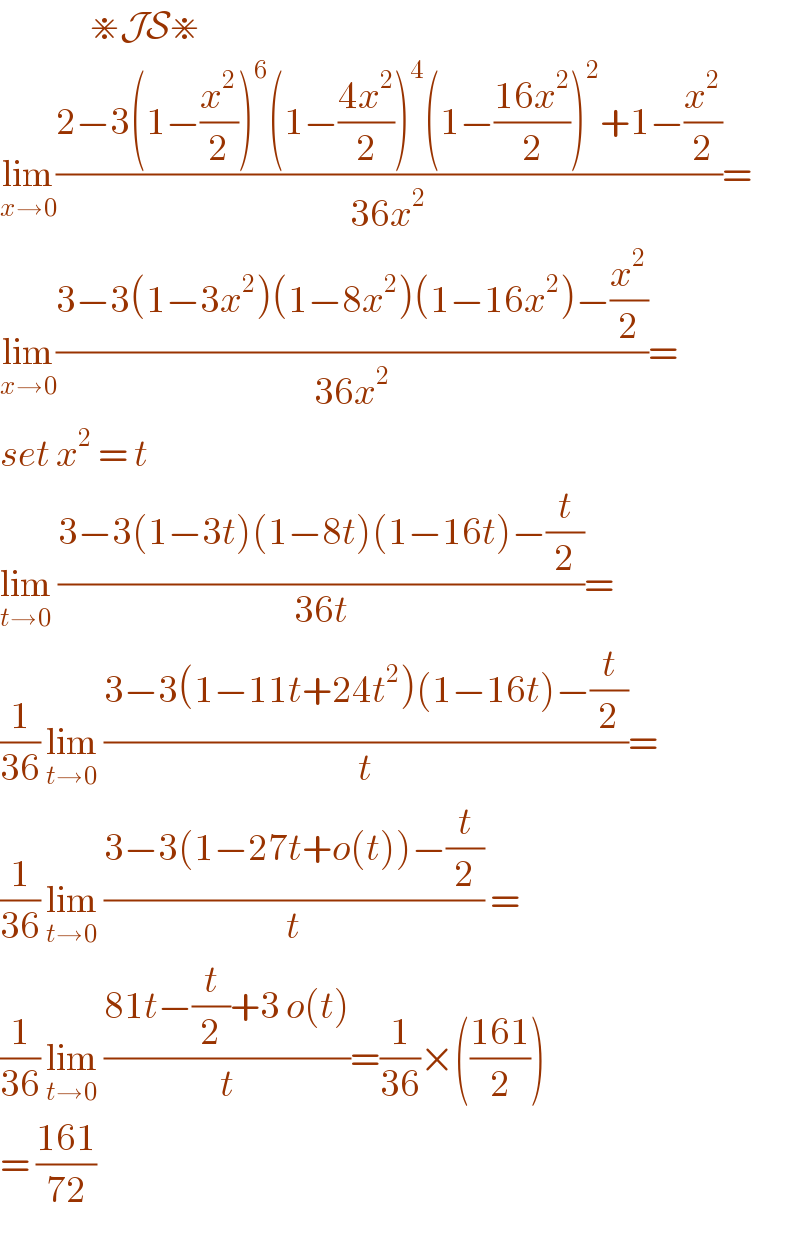
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{3}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{6}} \left(\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{4}} \left(\mathrm{1}−\frac{\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{36}{x}^{\mathrm{2}} }= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}−\mathrm{3}\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{8}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{16}{x}^{\mathrm{2}} \right)−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{36}{x}^{\mathrm{2}} }= \\ $$$${set}\:{x}^{\mathrm{2}} \:=\:{t} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}\left(\mathrm{1}−\mathrm{3}{t}\right)\left(\mathrm{1}−\mathrm{8}{t}\right)\left(\mathrm{1}−\mathrm{16}{t}\right)−\frac{{t}}{\mathrm{2}}}{\mathrm{36}{t}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{36}}\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}\left(\mathrm{1}−\mathrm{11}{t}+\mathrm{24}{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{16}{t}\right)−\frac{{t}}{\mathrm{2}}}{{t}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{36}}\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}\left(\mathrm{1}−\mathrm{27}{t}+{o}\left({t}\right)\right)−\frac{{t}}{\mathrm{2}}}{{t}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{36}}\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{81}{t}−\frac{{t}}{\mathrm{2}}+\mathrm{3}\:{o}\left({t}\right)}{{t}}=\frac{\mathrm{1}}{\mathrm{36}}×\left(\frac{\mathrm{161}}{\mathrm{2}}\right) \\ $$$$=\:\frac{\mathrm{161}}{\mathrm{72}} \\ $$
