Question Number 111092 by bemath last updated on 02/Sep/20
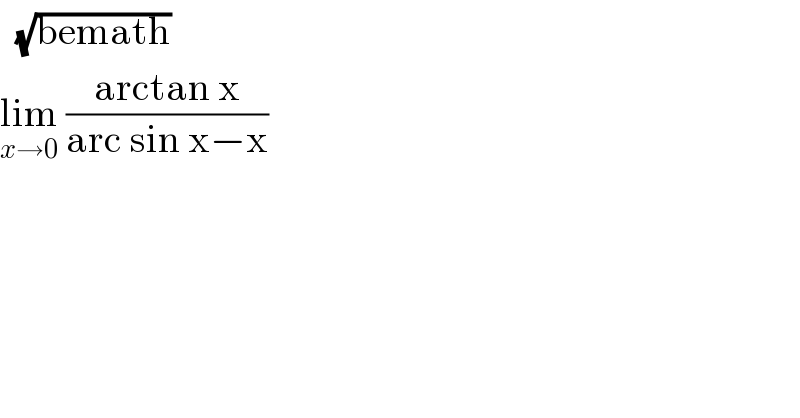
$$\:\:\sqrt{\mathrm{bemath}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{arctan}\:\mathrm{x}}{\mathrm{arc}\:\mathrm{sin}\:\mathrm{x}−\mathrm{x}} \\ $$
Commented by imsahil last updated on 02/Sep/20
How to write cube root?
Commented by bobhans last updated on 02/Sep/20

$$\sqrt[{\mathrm{3}\:\:}]{} \\ $$
Commented by Rasheed.Sindhi last updated on 02/Sep/20
Commented by Rasheed.Sindhi last updated on 02/Sep/20

$$@\:{imsahil} \\ $$$${To}\:{write}\:{cuberoot}\:{from}\:{the}\:{app}-{keyboard}. \\ $$$$\left(\mathrm{1}\right){click}\:\:\sqrt{\:\:}\:\:\left({marked}\:{by}\:\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right){click}\:{the}\:{button}\:{marked}\:{by}\:\mathrm{2} \\ $$$$\left(\mathrm{3}\right){write}\:\:“\:\mathrm{3}\:'' \\ $$
Answered by bobhans last updated on 02/Sep/20
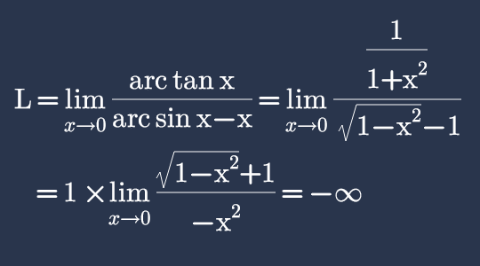
Commented by bemath last updated on 02/Sep/20
![it should be lim_(x→0) ((arc tan x)/(arc sin x−x)) = lim_(x→0) ((((1/(1+x^2 ))))/(((1/( (√(1−x^2 ))))−1))) = 1× lim_(x→0) [ ((√(1−x^2 ))/(1−(√(1−x^2 )))) ] = lim_(x→0) [((1.(1+(√(1−x^2 ))))/x^2 ) ]= ∞](https://www.tinkutara.com/question/Q111102.png)
$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{arc}\:\mathrm{tan}\:\mathrm{x}}{\mathrm{arc}\:\mathrm{sin}\:\mathrm{x}−\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)}{\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}−\mathrm{1}\right)} \\ $$$$=\:\mathrm{1}×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\:\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\right]\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}.\left(\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} }\:\right]=\:\infty\: \\ $$
Answered by ajfour last updated on 02/Sep/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)}{\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\mathrm{1}\right)} \\ $$
