bemath-lim-x-2-x-3-x-1-x-

Question Number 107207 by bemath last updated on 09/Aug/20

⊚ b e m a t h ⊚

\lim_{x \to \infty} {(2^{x} + 3^{x})}^{\frac{1}{x}} ?

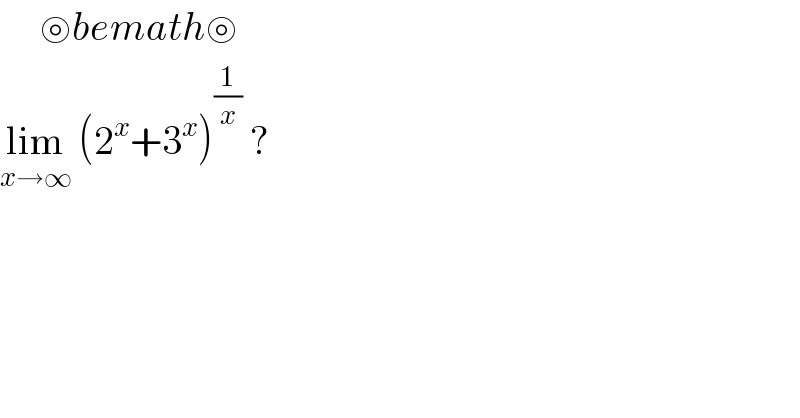
Answered by Dwaipayan Shikari last updated on 09/Aug/20

\underset{x \to \infty}{\lim 3} {(1 + {(\frac{2}{3})}^{x})}^{\frac{1}{x}} = \underset{x \to \infty}{\lim 3} {(1 + {(\frac{2}{3})}^{x})}^{\frac{1}{x} {(\frac{3}{2})}^{x} {(\frac{2}{3})}^{x}} = {\underset{x \to \infty}{\lim 3 e}}^{\frac{1}{x} . {(\frac{2}{3})}^{x}} = {3 e}^{0} = 3

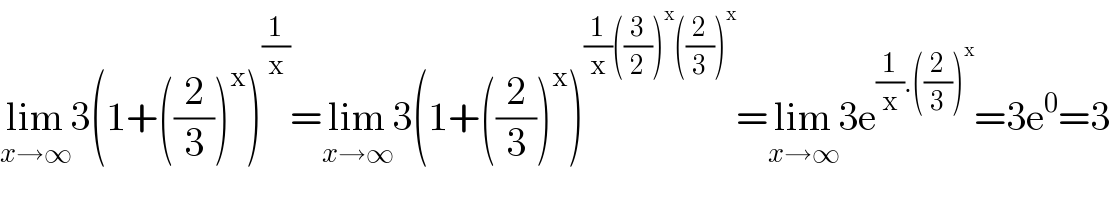
Answered by bemath last updated on 09/Aug/20

Answered by Dwaipayan Shikari last updated on 09/Aug/20

\lim_{x \to \infty} {(2^{x} + 3^{x})}^{\frac{1}{x}} = y

\frac{1}{x} \log (2^{x} + 3^{x}) = logy

\frac{1}{x} ({\log 3}^{x} + \log (1 + {(\frac{2}{3})}^{x})) = logy

\log 3 + \log (1 + {(\frac{2}{3})}^{x}) = logy

\log 3 = logy {(\frac{2}{3})}^{x} \to 0 (x \to \infty)

y = 3

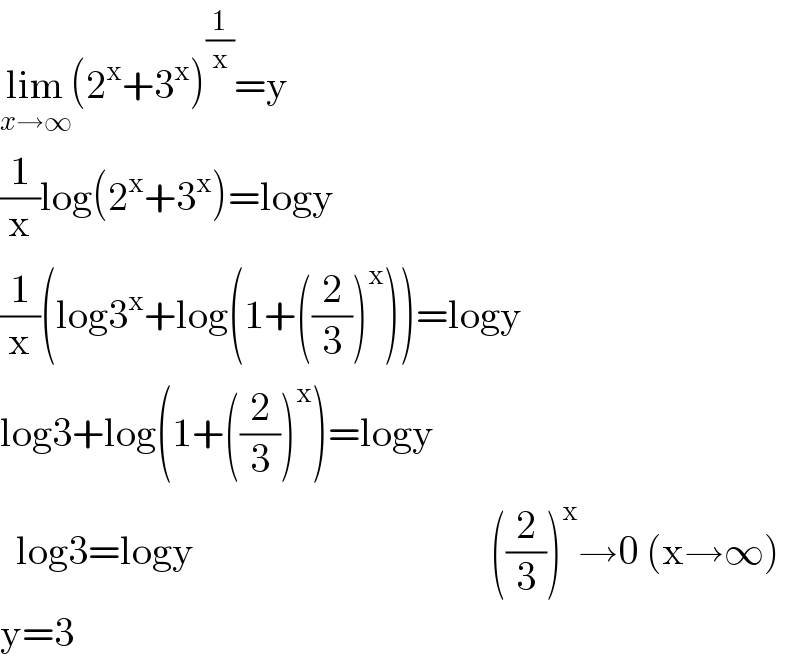
Answered by 1549442205PVT last updated on 10/Aug/20

\lim_{x \to \infty} {(2^{x} + 3^{x})}^{\frac{1}{x}} = \lim [3^{x} {(1 + {(\frac{2}{3})}^{x}]}^{\frac{1}{x}}

= l \underset{x \to \infty}{im} 3 . [{(1 + {(\frac{2}{3})}^{x}]}^{\frac{1}{x}} =

3 . \lim_{x \to \infty} [{(1 + {(\frac{2}{3})}^{x}]}^{\frac{1}{x}} = 3 . {[1 + {(\frac{2}{3})}^{\infty}]}^{\frac{1}{\infty}}

= 3 . {(1 + 0)}^{0} = 3.1 = 3