Question Number 107534 by bemath last updated on 11/Aug/20
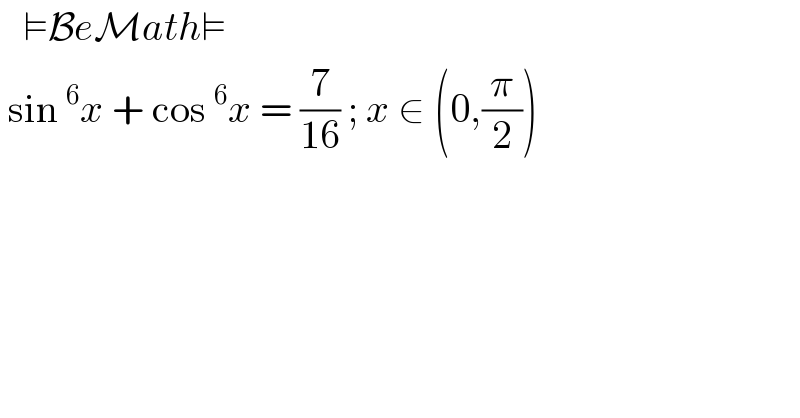
$$\:\:\:\vDash\mathcal{B}{e}\mathcal{M}{ath}\vDash \\ $$$$\:\mathrm{sin}\:^{\mathrm{6}} {x}\:+\:\mathrm{cos}\:^{\mathrm{6}} {x}\:=\:\frac{\mathrm{7}}{\mathrm{16}}\:;\:{x}\:\in\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right) \\ $$
Commented by hgrocks last updated on 11/Aug/20
7 and 16 both my favorite numbers ����
Commented by bemath last updated on 11/Aug/20

$${thank}\:{you}\:{all}\:{sir} \\ $$
Answered by Rio Michael last updated on 11/Aug/20
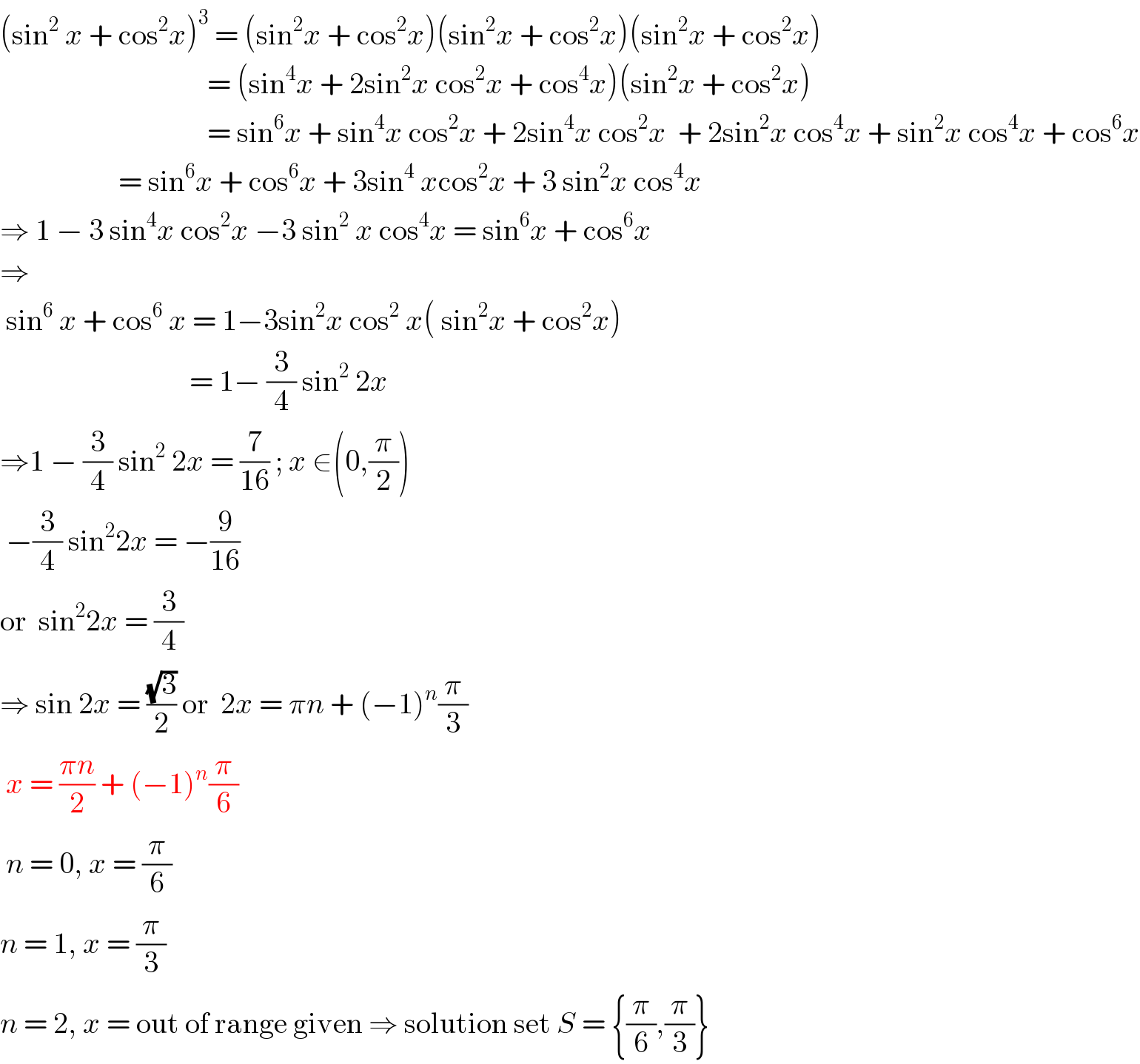
$$\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \:=\:\left(\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right)\left(\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right)\left(\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{sin}^{\mathrm{4}} {x}\:+\:\mathrm{2sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{4}} {x}\right)\left(\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{sin}^{\mathrm{6}} {x}\:+\:\mathrm{sin}^{\mathrm{4}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}\:+\:\mathrm{2sin}^{\mathrm{4}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}\:\:+\:\mathrm{2sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{4}} {x}\:+\:\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{4}} {x}\:+\:\mathrm{cos}^{\mathrm{6}} {x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{sin}^{\mathrm{6}} {x}\:+\:\mathrm{cos}^{\mathrm{6}} {x}\:+\:\mathrm{3sin}^{\mathrm{4}} \:{x}\mathrm{cos}^{\mathrm{2}} {x}\:+\:\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{4}} {x} \\ $$$$\Rightarrow\:\mathrm{1}\:−\:\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}\:−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{4}} {x}\:=\:\mathrm{sin}^{\mathrm{6}} {x}\:+\:\mathrm{cos}^{\mathrm{6}} {x} \\ $$$$\Rightarrow \\ $$$$\:\mathrm{sin}^{\mathrm{6}} \:{x}\:+\:\mathrm{cos}^{\mathrm{6}} \:{x}\:=\:\mathrm{1}−\mathrm{3sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\left(\:\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{cos}^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x} \\ $$$$\Rightarrow\mathrm{1}\:−\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\:=\:\frac{\mathrm{7}}{\mathrm{16}}\:;\:{x}\:\in\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:−\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}\:=\:−\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\mathrm{or}\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{2}{x}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{or}\:\:\mathrm{2}{x}\:=\:\pi{n}\:+\:\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{3}} \\ $$$$\:{x}\:=\:\frac{\pi{n}}{\mathrm{2}}\:+\:\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{6}} \\ $$$$\:{n}\:=\:\mathrm{0},\:{x}\:=\:\frac{\pi}{\mathrm{6}} \\ $$$${n}\:=\:\mathrm{1},\:{x}\:=\:\frac{\pi}{\mathrm{3}} \\ $$$${n}\:=\:\mathrm{2},\:{x}\:=\:\mathrm{out}\:\mathrm{of}\:\mathrm{range}\:\mathrm{given}\:\Rightarrow\:\mathrm{solution}\:\mathrm{set}\:{S}\:=\:\left\{\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{3}}\right\} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Aug/20
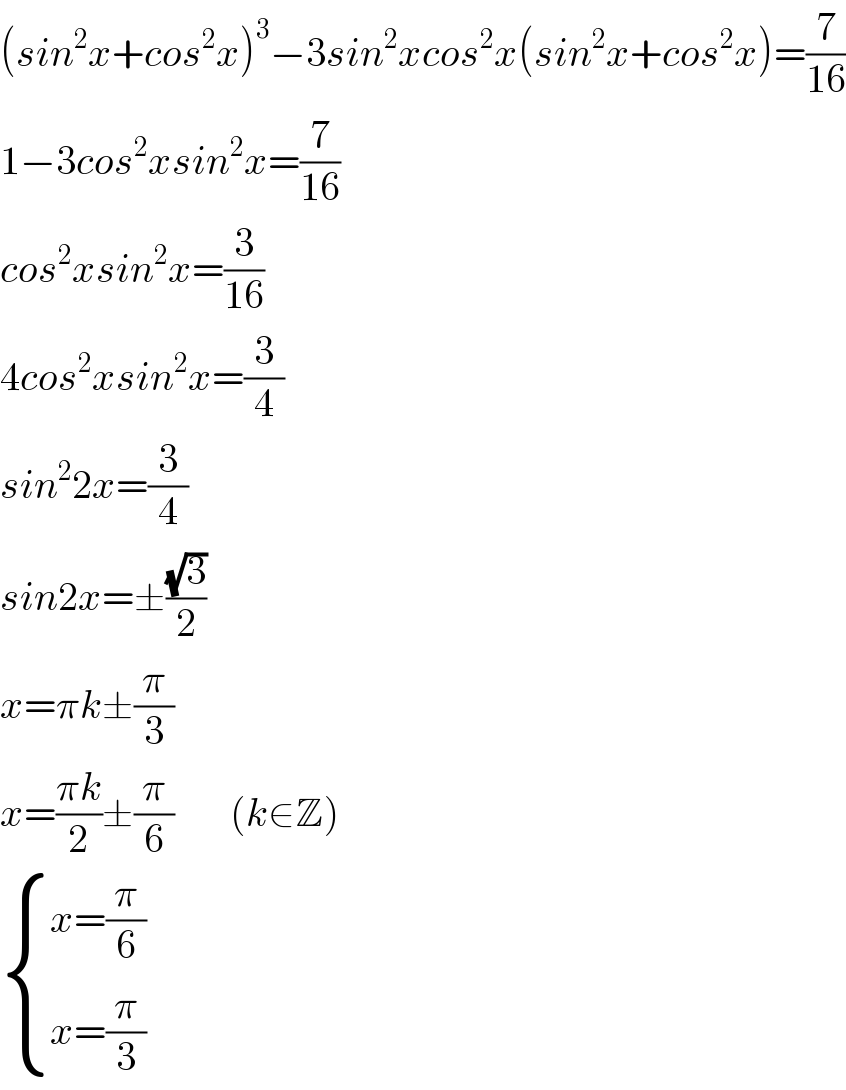
$$\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)=\frac{\mathrm{7}}{\mathrm{16}} \\ $$$$\mathrm{1}−\mathrm{3}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}=\frac{\mathrm{7}}{\mathrm{16}} \\ $$$${cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}=\frac{\mathrm{3}}{\mathrm{16}} \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${sin}^{\mathrm{2}} \mathrm{2}{x}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${sin}\mathrm{2}{x}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\pi{k}\pm\frac{\pi}{\mathrm{3}} \\ $$$${x}=\frac{\pi{k}}{\mathrm{2}}\pm\frac{\pi}{\mathrm{6}}\:\:\:\:\:\:\:\left({k}\in\mathbb{Z}\right) \\ $$$$\begin{cases}{{x}=\frac{\pi}{\mathrm{6}}}\\{{x}=\frac{\pi}{\mathrm{3}}}\end{cases} \\ $$
Answered by Sarah85 last updated on 11/Aug/20
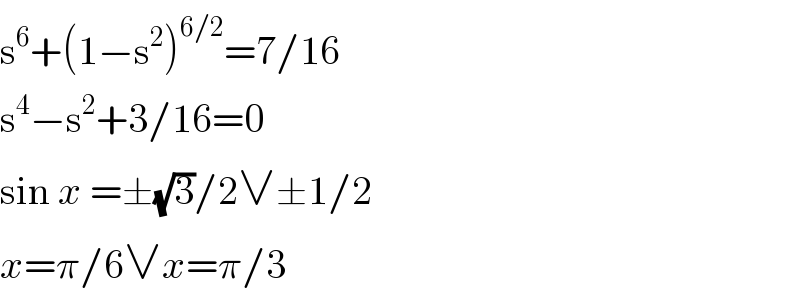
$$\mathrm{s}^{\mathrm{6}} +\left(\mathrm{1}−\mathrm{s}^{\mathrm{2}} \right)^{\mathrm{6}/\mathrm{2}} =\mathrm{7}/\mathrm{16} \\ $$$$\mathrm{s}^{\mathrm{4}} −\mathrm{s}^{\mathrm{2}} +\mathrm{3}/\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\:=\pm\sqrt{\mathrm{3}}/\mathrm{2}\vee\pm\mathrm{1}/\mathrm{2} \\ $$$${x}=\pi/\mathrm{6}\vee{x}=\pi/\mathrm{3} \\ $$
Answered by john santu last updated on 11/Aug/20
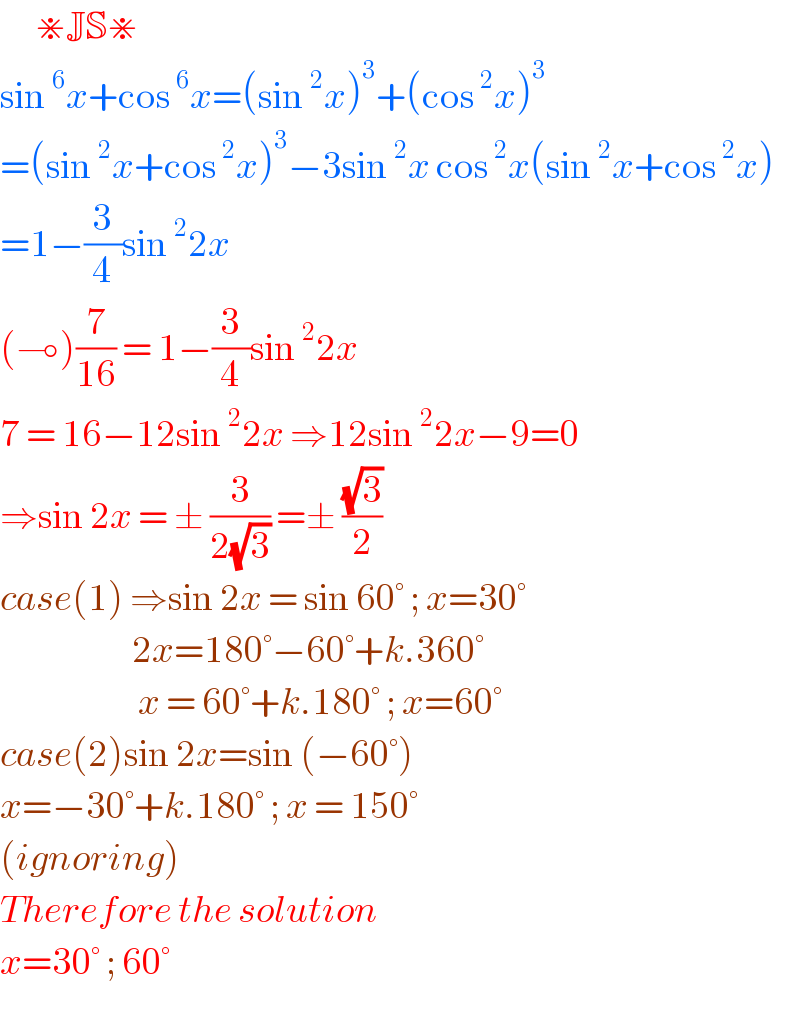
$$\:\:\:\:\:\:\divideontimes\mathbb{JS}\divideontimes \\ $$$$\mathrm{sin}\:^{\mathrm{6}} {x}+\mathrm{cos}\:^{\mathrm{6}} {x}=\left(\mathrm{sin}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} +\left(\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}\left(\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\: \\ $$$$\left(\multimap\right)\frac{\mathrm{7}}{\mathrm{16}}\:=\:\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\mathrm{7}\:=\:\mathrm{16}−\mathrm{12sin}\:^{\mathrm{2}} \mathrm{2}{x}\:\Rightarrow\mathrm{12sin}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}{x}\:=\:\pm\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\pm\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${case}\left(\mathrm{1}\right)\:\Rightarrow\mathrm{sin}\:\mathrm{2}{x}\:=\:\mathrm{sin}\:\mathrm{60}°\:;\:{x}=\mathrm{30}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}=\mathrm{180}°−\mathrm{60}°+{k}.\mathrm{360}°\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:=\:\mathrm{60}°+{k}.\mathrm{180}°\:;\:{x}=\mathrm{60}° \\ $$$${case}\left(\mathrm{2}\right)\mathrm{sin}\:\mathrm{2}{x}=\mathrm{sin}\:\left(−\mathrm{60}°\right) \\ $$$${x}=−\mathrm{30}°+{k}.\mathrm{180}°\:;\:{x}\:=\:\mathrm{150}° \\ $$$$\left({ignoring}\right) \\ $$$${Therefore}\:{the}\:{solution}\: \\ $$$${x}=\mathrm{30}°\:;\:\mathrm{60}°\: \\ $$
Answered by Her_Majesty last updated on 11/Aug/20
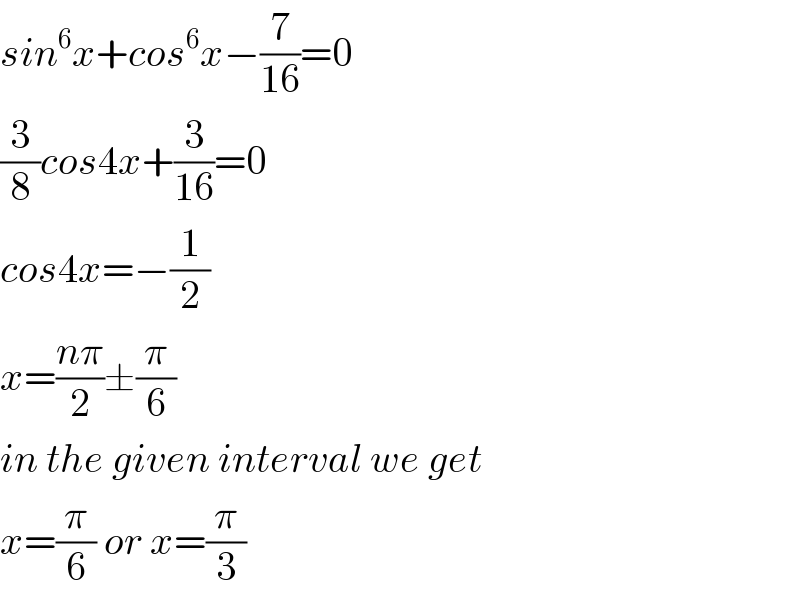
$${sin}^{\mathrm{6}} {x}+{cos}^{\mathrm{6}} {x}−\frac{\mathrm{7}}{\mathrm{16}}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{\mathrm{8}}{cos}\mathrm{4}{x}+\frac{\mathrm{3}}{\mathrm{16}}=\mathrm{0} \\ $$$${cos}\mathrm{4}{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}=\frac{{n}\pi}{\mathrm{2}}\pm\frac{\pi}{\mathrm{6}} \\ $$$${in}\:{the}\:{given}\:{interval}\:{we}\:{get} \\ $$$${x}=\frac{\pi}{\mathrm{6}}\:{or}\:{x}=\frac{\pi}{\mathrm{3}} \\ $$
