Menu Close

bemath-sin-x-sin-3-x-cos-3-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 107238 by bemath last updated on 09/Aug/20
⊞bemath⊞ ∫ ((sin x)/(sin^3 x+cos^3 x)) dx ?
$$\:\:\:\:\:\:\:\boxplus{bemath}\boxplus \\ $$$$\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}}\:{dx}\:?\: \\ $$
Answered by john santu last updated on 09/Aug/20
⋇JS⋇ ∫ ((csc^2 x )/(1+cot^3 x)) dx = −∫ ((d(cot x))/(1+cot^3 x)) =−∫(dv/(1+v^3 )) [ with v = cot x ] = −∫ ((1−v^2 )/(1+v^3 )) dv −(1/3)∫ ((d(1+v^3 ))/(1+v^3 )) =−(1/2)∫ ((1+(1−2v))/(1+v^3 ))dv−(1/3)ln ∣1+v^3 ∣ =−(1/2)∫ (dv/((v−(1/2))^2 +(((√3)/2))^2 )) +(1/2)∫ ((d(1−v+v^2 ))/(1−v))−(1/3)ln ∣1+v^3 ∣ = −(1/( (√3))) arc tan (((2cot x−1)/( (√3))))+(1/6)ln ∣1−cot x+cot^2 x∣−(1/3)ln ∣1+cot x∣ + C
$$\:\:\:\:\divideontimes\mathrm{JS}\divideontimes \\ $$$$\int\:\frac{\mathrm{csc}^{\mathrm{2}} \:\mathrm{x}\:}{\mathrm{1}+\mathrm{cot}\:^{\mathrm{3}} \mathrm{x}}\:\mathrm{dx}\:=\:−\int\:\frac{\mathrm{d}\left(\mathrm{cot}\:\mathrm{x}\right)}{\mathrm{1}+\mathrm{cot}\:^{\mathrm{3}} \mathrm{x}} \\ $$$$=−\int\frac{\mathrm{dv}}{\mathrm{1}+\mathrm{v}^{\mathrm{3}} }\:\left[\:\mathrm{with}\:\mathrm{v}\:=\:\mathrm{cot}\:\mathrm{x}\:\right] \\ $$$$=\:−\int\:\frac{\mathrm{1}−\mathrm{v}^{\mathrm{2}} }{\mathrm{1}+\mathrm{v}^{\mathrm{3}} }\:\mathrm{dv}\:−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{v}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{v}^{\mathrm{3}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}+\left(\mathrm{1}−\mathrm{2v}\right)}{\mathrm{1}+\mathrm{v}^{\mathrm{3}} }\mathrm{dv}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid\mathrm{1}+\mathrm{v}^{\mathrm{3}} \mid \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dv}}{\left(\mathrm{v}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{1}−\mathrm{v}+\mathrm{v}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{v}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln} \\ $$$$\mid\mathrm{1}+\mathrm{v}^{\mathrm{3}} \mid \\ $$$$=\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{2cot}\:\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln} \\ $$$$\mid\mathrm{1}−\mathrm{cot}\:\mathrm{x}+\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid\mathrm{1}+\mathrm{cot}\:\mathrm{x}\mid \\ $$$$+\:\mathrm{C}\: \\ $$
Answered by som(math1967) last updated on 09/Aug/20
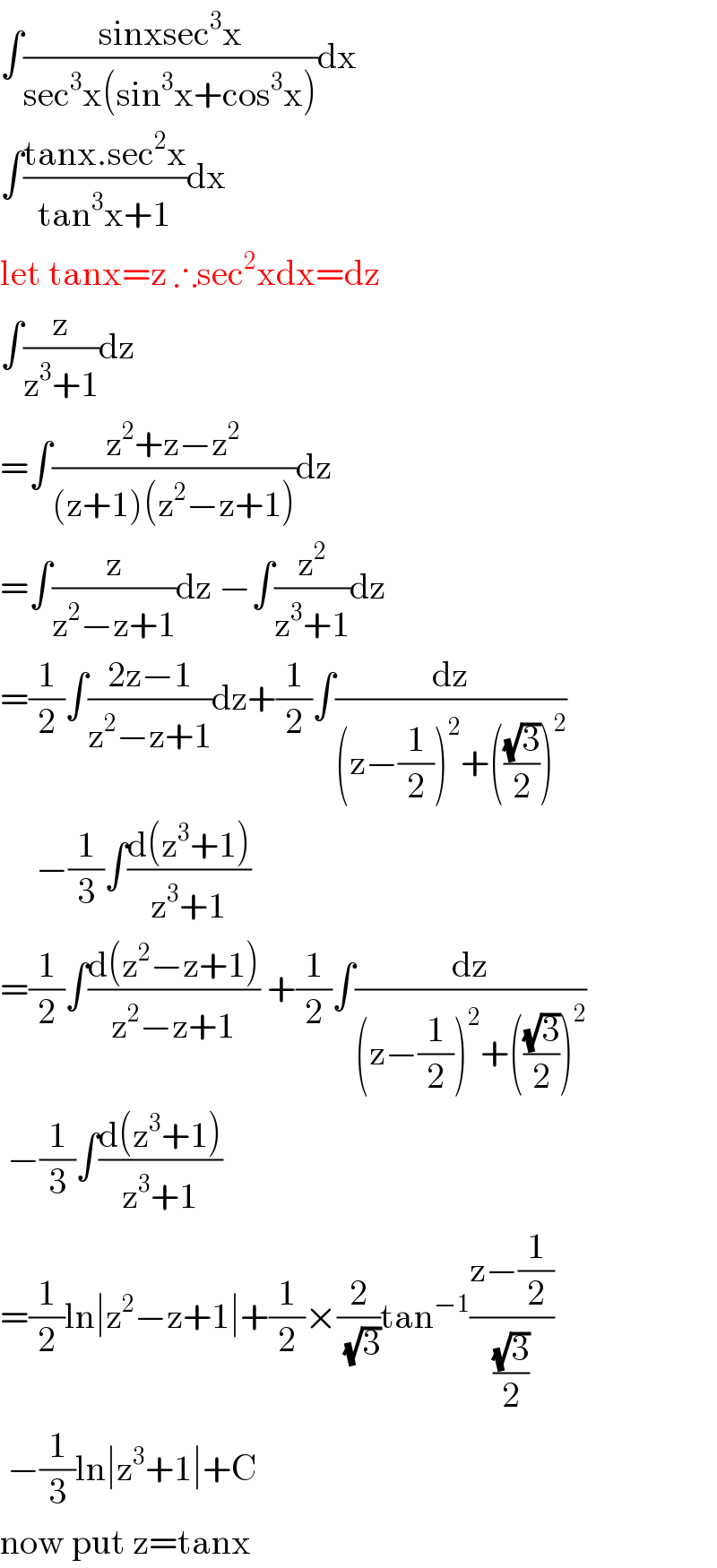
∫((sinxsec^3 x)/(sec^3 x(sin^3 x+cos^3 x)))dx ∫((tanx.sec^2 x)/(tan^3 x+1))dx let tanx=z ∴sec^2 xdx=dz ∫(z/(z^3 +1))dz =∫((z^2 +z−z^2 )/((z+1)(z^2 −z+1)))dz =∫(z/(z^2 −z+1))dz −∫(z^2 /(z^3 +1))dz =(1/2)∫((2z−1)/(z^2 −z+1))dz+(1/2)∫(dz/((z−(1/2))^2 +(((√3)/2))^2 )) −(1/3)∫((d(z^3 +1))/(z^3 +1)) =(1/2)∫((d(z^2 −z+1))/(z^2 −z+1)) +(1/2)∫(dz/((z−(1/2))^2 +(((√3)/2))^2 )) −(1/3)∫((d(z^3 +1))/(z^3 +1)) =(1/2)ln∣z^2 −z+1∣+(1/2)×(2/( (√3)))tan^(−1) ((z−(1/2))/((√3)/2)) −(1/3)ln∣z^3 +1∣+C now put z=tanx
$$\int\frac{\mathrm{sinxsec}^{\mathrm{3}} \mathrm{x}}{\mathrm{sec}^{\mathrm{3}} \mathrm{x}\left(\mathrm{sin}^{\mathrm{3}} \mathrm{x}+\mathrm{cos}^{\mathrm{3}} \mathrm{x}\right)}\mathrm{dx} \\ $$$$\int\frac{\mathrm{tanx}.\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{tan}^{\mathrm{3}} \mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{tanx}=\mathrm{z}\:\therefore\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{dz} \\ $$$$\int\frac{\mathrm{z}}{\mathrm{z}^{\mathrm{3}} +\mathrm{1}}\mathrm{dz} \\ $$$$=\int\frac{\mathrm{z}^{\mathrm{2}} +\mathrm{z}−\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}+\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)}\mathrm{dz} \\ $$$$=\int\frac{\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}}\mathrm{dz}\:−\int\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{3}} +\mathrm{1}}\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2z}−\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}}\mathrm{dz}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dz}}{\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{d}\left(\mathrm{z}^{\mathrm{3}} +\mathrm{1}\right)}{\mathrm{z}^{\mathrm{3}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)}{\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dz}}{\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{d}\left(\mathrm{z}^{\mathrm{3}} +\mathrm{1}\right)}{\mathrm{z}^{\mathrm{3}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{z}^{\mathrm{3}} +\mathrm{1}\mid+\mathrm{C} \\ $$$$\mathrm{now}\:\mathrm{put}\:\mathrm{z}=\mathrm{tanx} \\ $$
Answered by abdomathmax last updated on 09/Aug/20
I =∫ ((sinx)/(sin^3 x +cos^3 x))dx ⇒I =∫ ((sinx dx)/((sinx +cosx)(sin^2 x−cosxsinx +cos^2 x))) =∫ ((sinx dx)/((sinx +cosx)(1−cosx sinx))) =∫ (dx/((1+(1/(tanx)))(1−(1/2)sin(2x)))) =∫ ((tanx dx)/((1+tanx)(1−(1/2)×((2tanx)/(1+tan^2 x))))) =_(tanx =t) ∫ (t/((1+t)(1−(t/(1+t^2 )))))×(dt/(1+t^2 )) =∫ ((tdt)/((t+1)(1+t^2 −t))) =∫ ((tdt)/((t+1)(t^2 −t +1))) let decompose F(t) =(t/((t+1)(t^2 −t+1))) ⇒ F(t) =(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =((−1)/3) , lim_(t→+∞) tF(t) =0 =a+b ⇒b =(1/3) ⇒ F(t)=((−1)/(3(t+1))) +(((t/3)+c)/(t^2 −t +1)) F(0) =0 =−(1/3) +c ⇒c =(1/3) ⇒ F(t) =−(1/(3(t+1))) +(1/3)((t+1)/(t^2 −t +1)) ⇒ ∫ F(t)dt =((−1)/3)ln∣t+1∣+(1/6)∫ ((2t−1+3)/(t^2 −t+1))dt =−(1/3)ln∣t+1∣+(1/6)ln(t^2 −t+1)+(1/2)∫(dt/(t^2 −t+1)) ∫ (dt/(t^2 −t+1)) =∫ (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) =(4/3)∫ (1/(u^2 +1))((√3)/2)du =(2/( (√3))) arctan(((2t−1)/( (√3)))) +C ⇒ I =−(1/3)ln∣t+1∣+(1/6)ln(t^2 −t+1)+(1/( (√3))) arctan(((2t−1)/( (√3)))) +C =−(1/3)ln∣1+tanx∣+(1/6)ln(tan^2 x−tanx +1) +(1/( (√3))) arctan(((2tanx−1)/( (√3))))+C
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{sinx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}\:+\mathrm{cos}^{\mathrm{3}} \mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int\:\frac{\mathrm{sinx}\:\mathrm{dx}}{\left(\mathrm{sinx}\:+\mathrm{cosx}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cosxsinx}\:+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$=\int\:\:\frac{\mathrm{sinx}\:\mathrm{dx}}{\left(\mathrm{sinx}\:+\mathrm{cosx}\right)\left(\mathrm{1}−\mathrm{cosx}\:\mathrm{sinx}\right)} \\ $$$$=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tanx}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\right)} \\ $$$$=\int\:\:\:\frac{\mathrm{tanx}\:\mathrm{dx}}{\left(\mathrm{1}+\mathrm{tanx}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2tanx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\right)} \\ $$$$=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\:\:\int\:\:\:\frac{\mathrm{t}}{\left(\mathrm{1}+\mathrm{t}\right)\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{\mathrm{tdt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{t}\right)}\:=\int\:\frac{\mathrm{tdt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}\right)} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{bt}\:+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}} \\ $$$$\mathrm{a}\:=\frac{−\mathrm{1}}{\mathrm{3}}\:\:\:,\:\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{−\mathrm{1}}{\mathrm{3}\left(\mathrm{t}+\mathrm{1}\right)}\:+\frac{\frac{\mathrm{t}}{\mathrm{3}}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{t}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}}\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\frac{−\mathrm{1}}{\mathrm{3}}\boldsymbol{\mathrm{ln}}\mid\mathrm{t}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{6}}\int\:\frac{\mathrm{2t}−\mathrm{1}+\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{t}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\boldsymbol{\mathrm{t}}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}} \\ $$$$\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\:=\int\:\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\:=_{\boldsymbol{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\boldsymbol{\mathrm{u}}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int\:\:\:\:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{du}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{t}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{1}+\mathrm{tanx}\mid+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{tanx}\:+\mathrm{1}\right) \\ $$$$+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2tanx}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *