Question Number 108605 by bemath last updated on 18/Aug/20
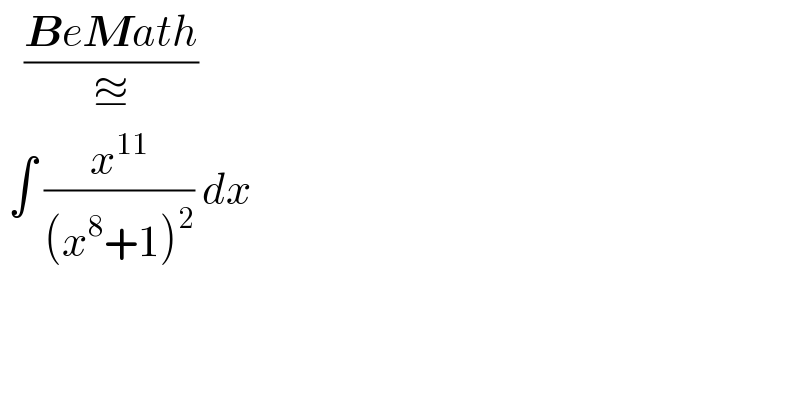
$$\:\:\:\frac{\boldsymbol{{B}}{e}\boldsymbol{{M}}{ath}}{\approxeq} \\ $$$$\:\int\:\frac{{x}^{\mathrm{11}} }{\left({x}^{\mathrm{8}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\: \\ $$
Answered by bemath last updated on 18/Aug/20
![let x^4 = tan v ⇒4x^3 dx=sec^2 v dv I=(1/4)∫ ((x^8 (4x^3 dx))/((x^8 +1)^2 )) =(1/4) ∫ ((tan^2 v sec^2 v dv)/(sec^4 v)) I= (1/4)∫ ((tan^2 v)/(sec^2 v)) dv = (1/4)∫sin^2 v dv I=(1/8)∫(1−cos 2v)dv I=(1/8)v−(1/8)sin v cos v + c I=(1/8) [tan^(−1) (x^4 )−(x^4 /(x^8 +1)) ] + c](https://www.tinkutara.com/question/Q108606.png)
$$\:\:{let}\:{x}^{\mathrm{4}} \:=\:\mathrm{tan}\:{v}\:\Rightarrow\mathrm{4}{x}^{\mathrm{3}} \:{dx}=\mathrm{sec}\:^{\mathrm{2}} {v}\:{dv} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{{x}^{\mathrm{8}} \left(\mathrm{4}{x}^{\mathrm{3}} \:{dx}\right)}{\left({x}^{\mathrm{8}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\frac{\mathrm{tan}\:^{\mathrm{2}} {v}\:\mathrm{sec}\:^{\mathrm{2}} {v}\:{dv}}{\mathrm{sec}\:^{\mathrm{4}} {v}} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{tan}\:^{\mathrm{2}} {v}}{\mathrm{sec}\:^{\mathrm{2}} {v}}\:{dv}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{sin}\:^{\mathrm{2}} {v}\:{dv} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{v}\right){dv} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}{v}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:{v}\:\mathrm{cos}\:{v}\:+\:{c} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}\:\left[\mathrm{tan}^{−\mathrm{1}} \left({x}^{\mathrm{4}} \right)−\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{8}} +\mathrm{1}}\:\right]\:+\:{c} \\ $$
Answered by malwan last updated on 18/Aug/20
![y=x^4 ⇒dy=4x^3 dx ⇒∫((x^8 ×x^3 )/(x^8 +1))dx=(1/4)∫(y^2 /(y^2 +1))dy =(1/4)∫((y^2 +1−1)/(y^2 +1)) dy =(1/4)∫[1−(1/(y^2 +1))]dy =(1/4)[y−tan^(−1) y]+ c =(1/4)[x^4 −tan^(−1) x^4 ]+ c](https://www.tinkutara.com/question/Q108607.png)
$${y}={x}^{\mathrm{4}} \Rightarrow{dy}=\mathrm{4}{x}^{\mathrm{3}} {dx} \\ $$$$\Rightarrow\int\frac{{x}^{\mathrm{8}} ×{x}^{\mathrm{3}} }{{x}^{\mathrm{8}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{y}^{\mathrm{2}} }{{y}^{\mathrm{2}} +\mathrm{1}}{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{y}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}\:{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left[\mathrm{1}−\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}\right]{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[{y}−{tan}^{−\mathrm{1}} {y}\right]+\:{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[{x}^{\mathrm{4}} −{tan}^{−\mathrm{1}} \:{x}^{\mathrm{4}} \:\right]+\:{c} \\ $$
Commented by bemath last updated on 18/Aug/20

$${cooll} \\ $$
