Question Number 107756 by bemath last updated on 12/Aug/20
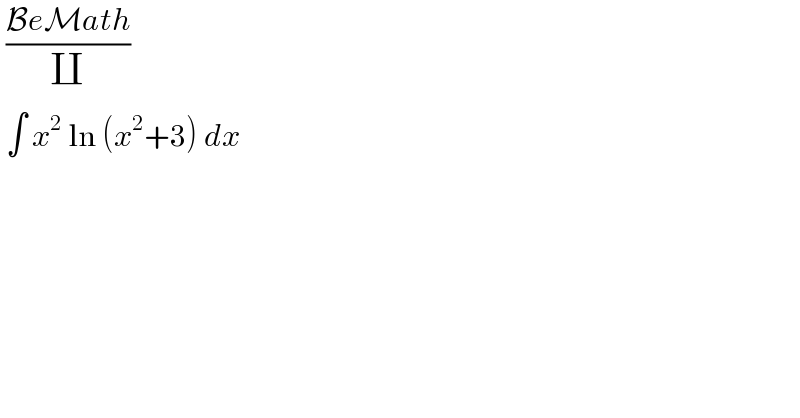
$$\:\frac{\mathcal{B}{e}\mathcal{M}{ath}}{\coprod} \\ $$$$\:\int\:{x}^{\mathrm{2}} \:\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{3}\right)\:{dx}\: \\ $$
Answered by hgrocks last updated on 12/Aug/20
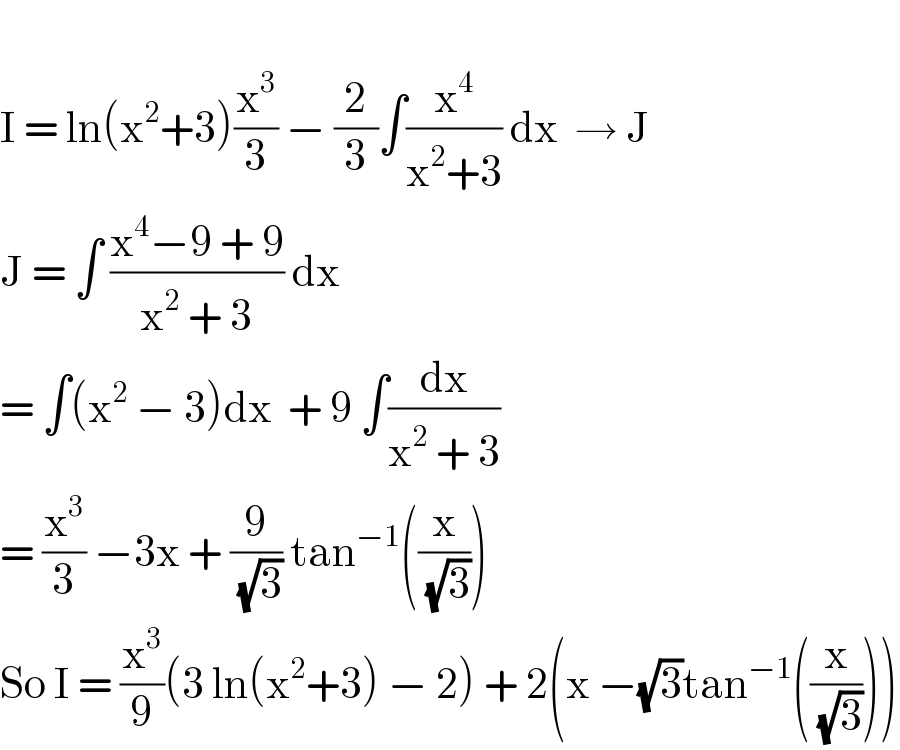
$$ \\ $$$$\mathrm{I}\:=\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:−\:\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\:\mathrm{dx}\:\:\rightarrow\:\mathrm{J} \\ $$$$\mathrm{J}\:=\:\int\:\frac{\mathrm{x}^{\mathrm{4}} −\mathrm{9}\:+\:\mathrm{9}}{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{3}}\:\mathrm{dx}\: \\ $$$$=\:\int\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{3}\right)\mathrm{dx}\:\:+\:\mathrm{9}\:\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{3}}\: \\ $$$$=\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:−\mathrm{3x}\:+\:\frac{\mathrm{9}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\mathrm{So}\:\mathrm{I}\:=\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{9}}\left(\mathrm{3}\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)\:−\:\mathrm{2}\right)\:+\:\mathrm{2}\left(\mathrm{x}\:−\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{3}}}\right)\right) \\ $$
Answered by bobhans last updated on 12/Aug/20
![((⊺Bobhans⊺)/Π) set ln (x^2 +3) = u ⇒ ((2x)/(x^2 +3)) dx = du v = (1/3)x^3 I=(1/3)x^3 ln (x^2 +3)−(1/3)∫ ((2x^4 )/((x^2 +3))) dx I=(1/3)x^3 ln (x^2 +3)−(2/3) ∫(x^4 /(x^2 +3)) dx I=(1/3)x^3 ln (x^2 +3)−(2/3)∫ (((x^2 +3)^2 −6x^2 −9)/(x^2 +3))dx I=(1/3)x^3 ln (x^2 +3)−(2/3)∫ ((x^2 +3)−((6(x^2 +3)+9)/(x^2 +3)))dx I=(1/3)x^3 ln (x^2 +3)−(2/3)[(1/3)x^3 +3x−6x+∫(9/(x^2 +3))dx] I=(1/3)x^3 ln (x^2 +3)−(2/9)x^3 +2x−2(√3) tan^(−1) ((x/( (√3))))+C](https://www.tinkutara.com/question/Q107762.png)
$$\:\:\:\:\:\:\frac{\intercal\mathcal{B}\mathrm{obhans}\intercal}{\Pi} \\ $$$$\mathrm{set}\:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)\:=\:\mathrm{u}\:\Rightarrow\:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\:\mathrm{dx}\:=\:\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\mathrm{v}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\:\:\:\:\:\:\: \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{2x}^{\mathrm{4}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)}\:\mathrm{dx}\:\: \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\:\int\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\:\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} −\mathrm{6x}^{\mathrm{2}} −\mathrm{9}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\int\:\left(\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{6}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)+\mathrm{9}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{6x}+\int\frac{\mathrm{9}}{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\mathrm{dx}\right] \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{x}^{\mathrm{3}} +\mathrm{2x}−\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{C} \\ $$$$ \\ $$
