Question Number 106787 by bemath last updated on 07/Aug/20
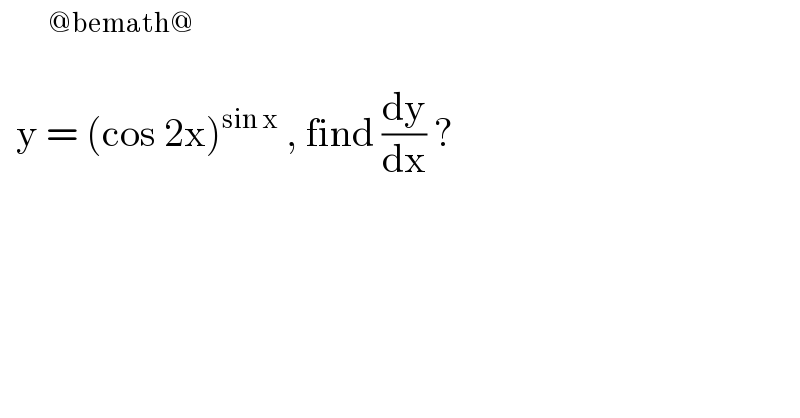
$$\:\:\:\:\:\:\overset{@\mathrm{bemath}@} {\:} \\ $$$$\:\:\mathrm{y}\:=\:\left(\mathrm{cos}\:\mathrm{2x}\right)^{\mathrm{sin}\:\mathrm{x}} \:,\:\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 07/Aug/20
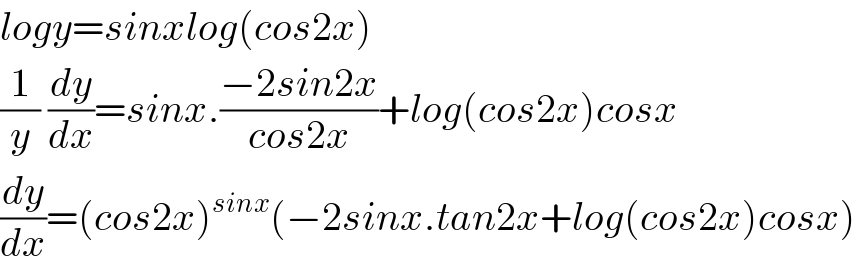
$${logy}={sinxlog}\left({cos}\mathrm{2}{x}\right) \\ $$$$\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}={sinx}.\frac{−\mathrm{2}{sin}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}+{log}\left({cos}\mathrm{2}{x}\right){cosx} \\ $$$$\frac{{dy}}{{dx}}=\left({cos}\mathrm{2}{x}\right)^{{sinx}} \left(−\mathrm{2}{sinx}.{tan}\mathrm{2}{x}+{log}\left({cos}\mathrm{2}{x}\right){cosx}\right) \\ $$
Answered by john santu last updated on 07/Aug/20
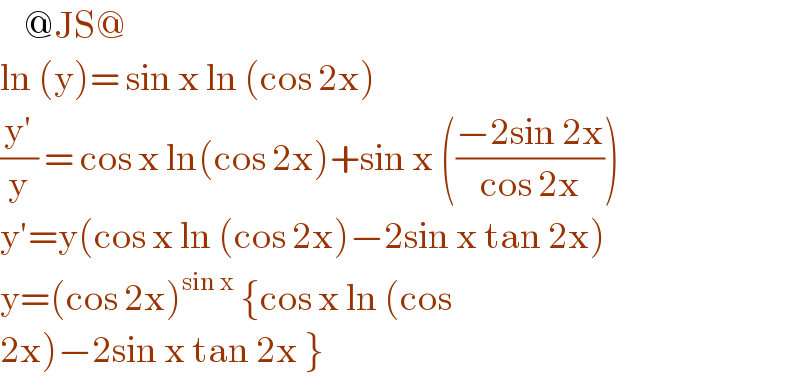
$$\:\:\:\:@\mathrm{JS}@ \\ $$$$\mathrm{ln}\:\left(\mathrm{y}\right)=\:\mathrm{sin}\:\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{cos}\:\mathrm{2x}\right) \\ $$$$\frac{\mathrm{y}'}{\mathrm{y}}\:=\:\mathrm{cos}\:\mathrm{x}\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{2x}\right)+\mathrm{sin}\:\mathrm{x}\:\left(\frac{−\mathrm{2sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{2x}}\right) \\ $$$$\mathrm{y}'=\mathrm{y}\left(\mathrm{cos}\:\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{cos}\:\mathrm{2x}\right)−\mathrm{2sin}\:\mathrm{x}\:\mathrm{tan}\:\mathrm{2x}\right) \\ $$$$\mathrm{y}=\left(\mathrm{cos}\:\mathrm{2x}\right)^{\mathrm{sin}\:\mathrm{x}} \:\left\{\mathrm{cos}\:\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{cos}\right.\right. \\ $$$$\left.\mathrm{2}\left.\mathrm{x}\right)−\mathrm{2sin}\:\mathrm{x}\:\mathrm{tan}\:\mathrm{2x}\:\right\}\: \\ $$
