Menu Close

bob-hans-1-lim-x-3-sin-x-9-x-tan-x-3-cos-9-x-x-2-x-tan-1-y-dx-x-2-2-1-y-2-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 110350 by bobhans last updated on 28/Aug/20
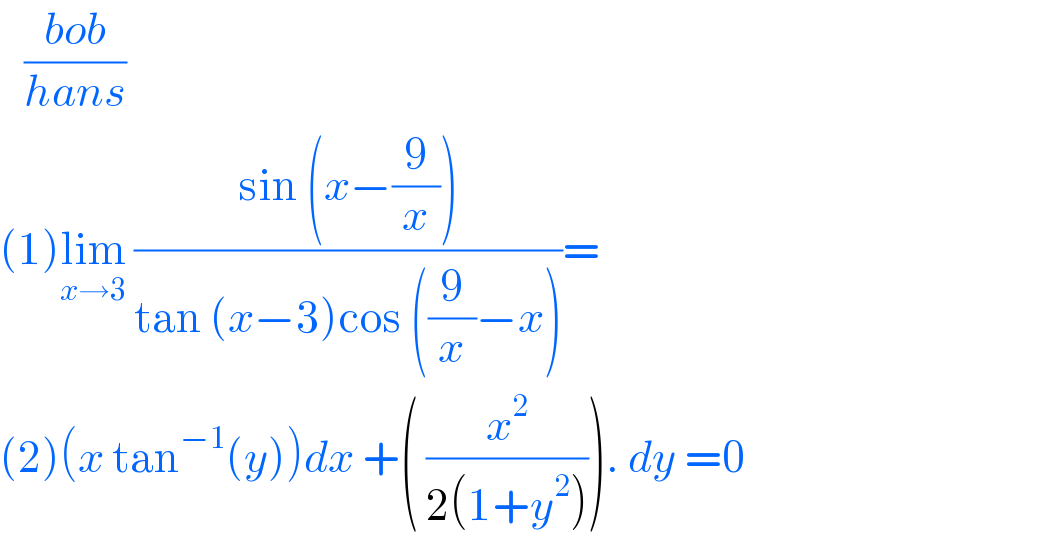
((bob)/(hans)) (1)lim_(x→3) ((sin (x−(9/x)))/(tan (x−3)cos ((9/x)−x)))= (2)(x tan^(−1) (y))dx +( (x^2 /(2(1+y^2 )))). dy =0
$$\:\:\:\frac{{bob}}{{hans}} \\ $$$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({x}−\frac{\mathrm{9}}{{x}}\right)}{\mathrm{tan}\:\left({x}−\mathrm{3}\right)\mathrm{cos}\:\left(\frac{\mathrm{9}}{{x}}−{x}\right)}= \\ $$$$\left(\mathrm{2}\right)\left({x}\:\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\right){dx}\:+\left(\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}\right).\:{dy}\:=\mathrm{0}\: \\ $$
Answered by john santu last updated on 28/Aug/20
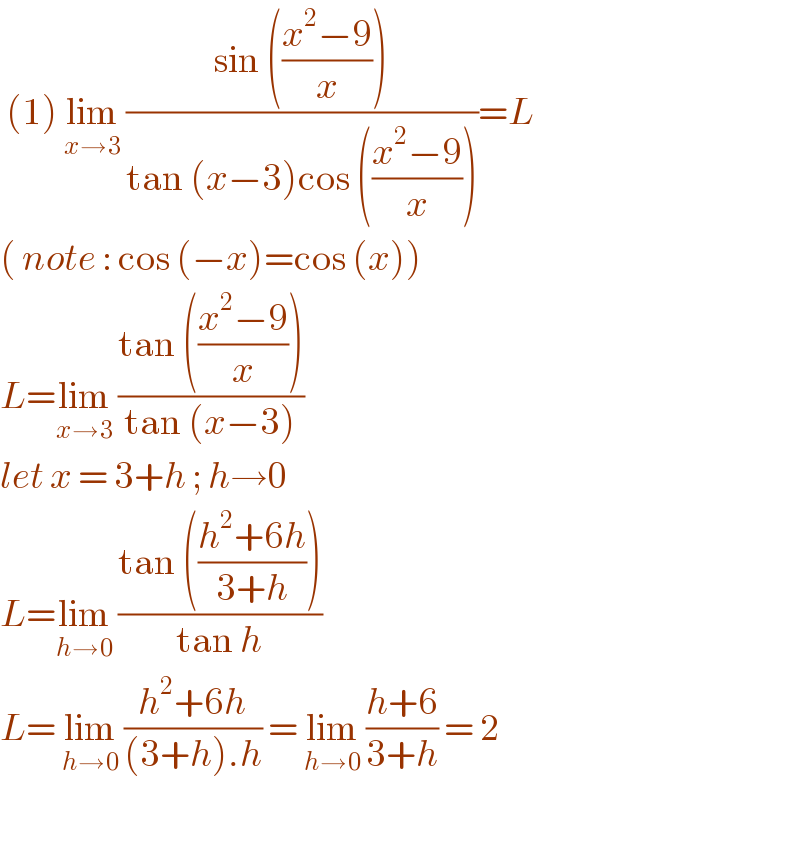
(1) lim_(x→3) ((sin (((x^2 −9)/x)))/(tan (x−3)cos (((x^2 −9)/x))))=L ( note : cos (−x)=cos (x)) L=lim_(x→3) ((tan (((x^2 −9)/x)))/(tan (x−3))) let x = 3+h ; h→0 L=lim_(h→0) ((tan (((h^2 +6h)/(3+h))))/(tan h)) L= lim_(h→0) ((h^2 +6h)/((3+h).h)) = lim_(h→0) ((h+6)/(3+h)) = 2
$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{{x}^{\mathrm{2}} −\mathrm{9}}{{x}}\right)}{\mathrm{tan}\:\left({x}−\mathrm{3}\right)\mathrm{cos}\:\left(\frac{{x}^{\mathrm{2}} −\mathrm{9}}{{x}}\right)}={L} \\ $$$$\left(\:{note}\::\:\mathrm{cos}\:\left(−{x}\right)=\mathrm{cos}\:\left({x}\right)\right) \\ $$$${L}=\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\frac{{x}^{\mathrm{2}} −\mathrm{9}}{{x}}\right)}{\mathrm{tan}\:\left({x}−\mathrm{3}\right)}\: \\ $$$${let}\:{x}\:=\:\mathrm{3}+{h}\:;\:{h}\rightarrow\mathrm{0} \\ $$$${L}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\frac{{h}^{\mathrm{2}} +\mathrm{6}{h}}{\mathrm{3}+{h}}\right)}{\mathrm{tan}\:{h}} \\ $$$${L}=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{h}^{\mathrm{2}} +\mathrm{6}{h}}{\left(\mathrm{3}+{h}\right).{h}}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{h}+\mathrm{6}}{\mathrm{3}+{h}}\:=\:\mathrm{2} \\ $$$$ \\ $$
Answered by john santu last updated on 28/Aug/20
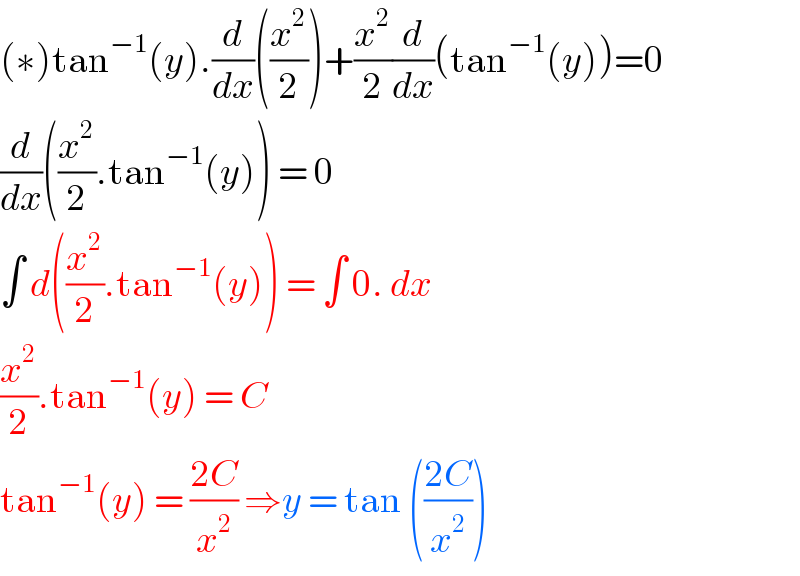
(∗)tan^(−1) (y).(d/dx)((x^2 /2))+(x^2 /2)(d/dx)(tan^(−1) (y))=0 (d/dx)((x^2 /2).tan^(−1) (y)) = 0 ∫ d((x^2 /2).tan^(−1) (y)) = ∫ 0. dx (x^2 /2).tan^(−1) (y) = C tan^(−1) (y) = ((2C)/x^2 ) ⇒y = tan (((2C)/x^2 ))
$$\left(\ast\right)\mathrm{tan}^{−\mathrm{1}} \left({y}\right).\frac{{d}}{{dx}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\frac{{d}}{{dx}}\left(\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\right)=\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}.\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\right)\:=\:\mathrm{0} \\ $$$$\int\:{d}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}.\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\right)\:=\:\int\:\mathrm{0}.\:{dx}\: \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}.\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\:=\:{C}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\:=\:\frac{\mathrm{2}{C}}{{x}^{\mathrm{2}} }\:\Rightarrow{y}\:=\:\mathrm{tan}\:\left(\frac{\mathrm{2}{C}}{{x}^{\mathrm{2}} }\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *