Question Number 107299 by bobhans last updated on 10/Aug/20
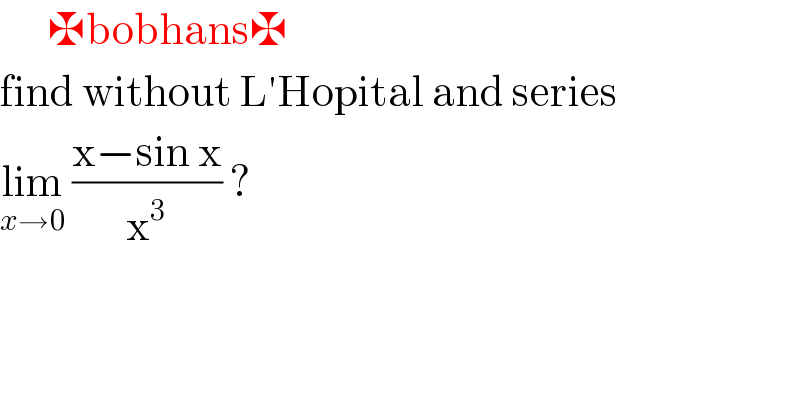
$$\:\:\:\:\:\:\maltese\mathrm{bobhans}\maltese \\ $$$$\mathrm{find}\:\mathrm{without}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{and}\:\mathrm{series}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\:? \\ $$
Answered by john santu last updated on 10/Aug/20
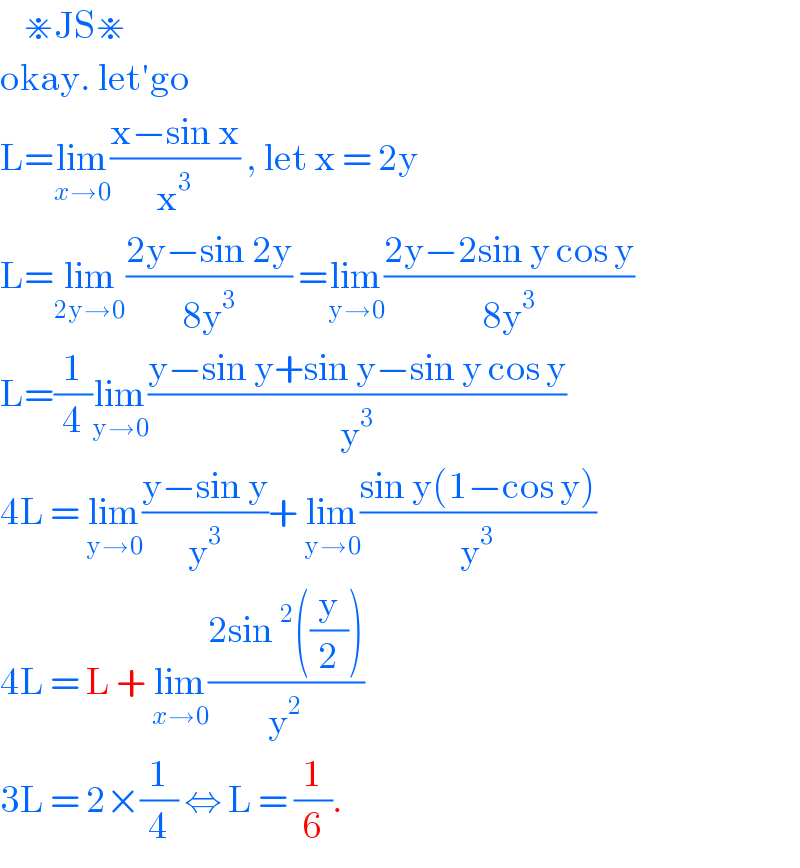
$$\:\:\:\:\divideontimes\mathrm{JS}\divideontimes \\ $$$$\mathrm{okay}.\:\mathrm{let}'\mathrm{go} \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\:,\:\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2y} \\ $$$$\mathrm{L}=\underset{\mathrm{2y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2y}−\mathrm{sin}\:\mathrm{2y}}{\mathrm{8y}^{\mathrm{3}} }\:=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2y}−\mathrm{2sin}\:\mathrm{y}\:\mathrm{cos}\:\mathrm{y}}{\mathrm{8y}^{\mathrm{3}} } \\ $$$$\mathrm{L}=\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{y}−\mathrm{sin}\:\mathrm{y}+\mathrm{sin}\:\mathrm{y}−\mathrm{sin}\:\mathrm{y}\:\mathrm{cos}\:\mathrm{y}}{\mathrm{y}^{\mathrm{3}} } \\ $$$$\mathrm{4L}\:=\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{y}−\mathrm{sin}\:\mathrm{y}}{\mathrm{y}^{\mathrm{3}} }+\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{y}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{y}\right)}{\mathrm{y}^{\mathrm{3}} } \\ $$$$\mathrm{4L}\:=\:\mathrm{L}\:+\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{y}}{\mathrm{2}}\right)}{\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{3L}\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}\:\Leftrightarrow\:\mathrm{L}\:=\:\frac{\mathrm{1}}{\mathrm{6}}. \\ $$
Commented by bemath last updated on 10/Aug/20

$${waw}…{great}\: \\ $$
Commented by bobhans last updated on 10/Aug/20

$$\mathrm{thAnk}\:\mathrm{you} \\ $$
Commented by malwaan last updated on 10/Aug/20

$${great}\:! \\ $$
Answered by $@y@m last updated on 10/Aug/20
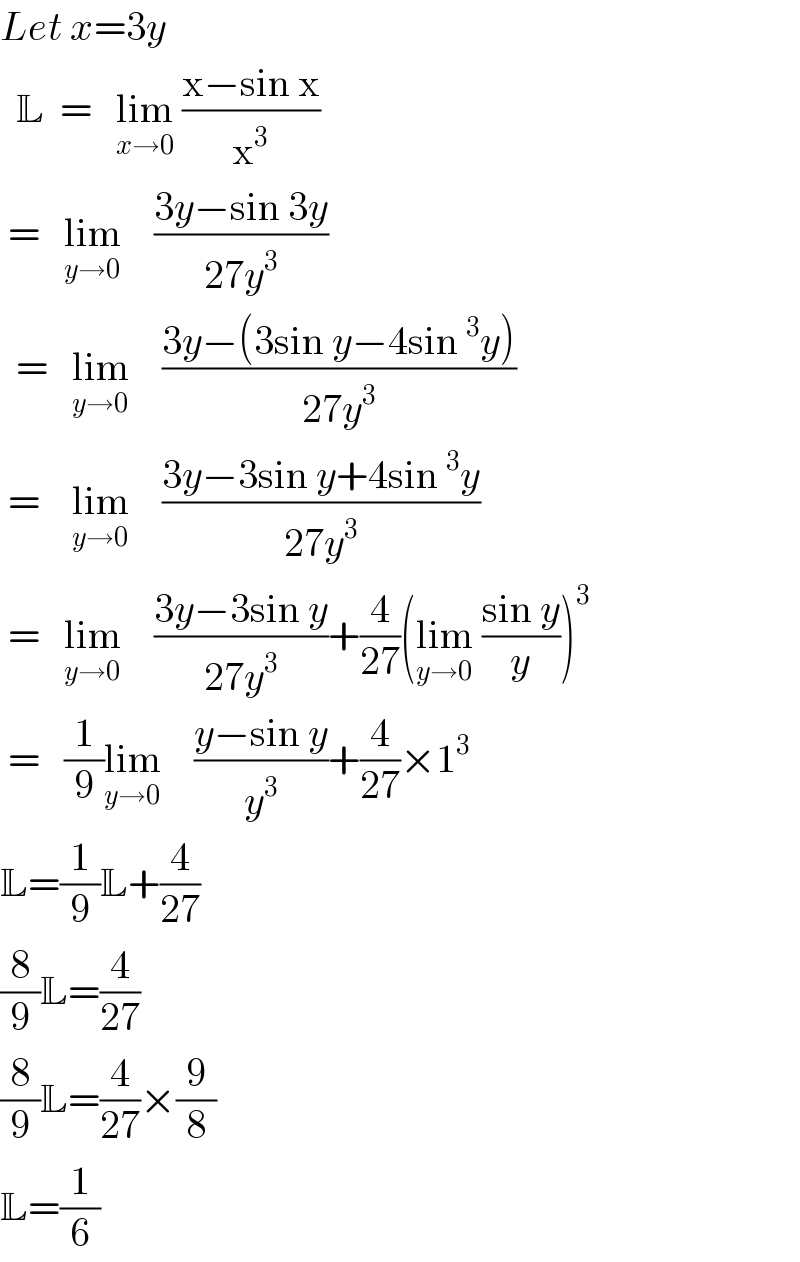
$${Let}\:{x}=\mathrm{3}{y} \\ $$$$\:\:\mathbb{L}\:\:=\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\: \\ $$$$\:=\:\:\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{3}{y}−\mathrm{sin}\:\mathrm{3}{y}}{\mathrm{27}{y}^{\mathrm{3}} } \\ $$$$\:\:=\:\:\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{3}{y}−\left(\mathrm{3sin}\:{y}−\mathrm{4sin}\:^{\mathrm{3}} {y}\right)}{\mathrm{27}{y}^{\mathrm{3}} } \\ $$$$\:=\:\:\:\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{3}{y}−\mathrm{3sin}\:{y}+\mathrm{4sin}\:^{\mathrm{3}} {y}}{\mathrm{27}{y}^{\mathrm{3}} } \\ $$$$\:=\:\:\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{3}{y}−\mathrm{3sin}\:{y}}{\mathrm{27}{y}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{27}}\left(\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{y}}{{y}}\right)^{\mathrm{3}} \\ $$$$\:=\:\:\:\frac{\mathrm{1}}{\mathrm{9}}\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{{y}−\mathrm{sin}\:{y}}{{y}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{27}}×\mathrm{1}^{\mathrm{3}} \\ $$$$\mathbb{L}=\frac{\mathrm{1}}{\mathrm{9}}\mathbb{L}+\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$\frac{\mathrm{8}}{\mathrm{9}}\mathbb{L}=\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$\frac{\mathrm{8}}{\mathrm{9}}\mathbb{L}=\frac{\mathrm{4}}{\mathrm{27}}×\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\mathbb{L}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by bemath last updated on 10/Aug/20

$${waw}…{great}…{too} \\ $$
