Question Number 108401 by bobhans last updated on 16/Aug/20
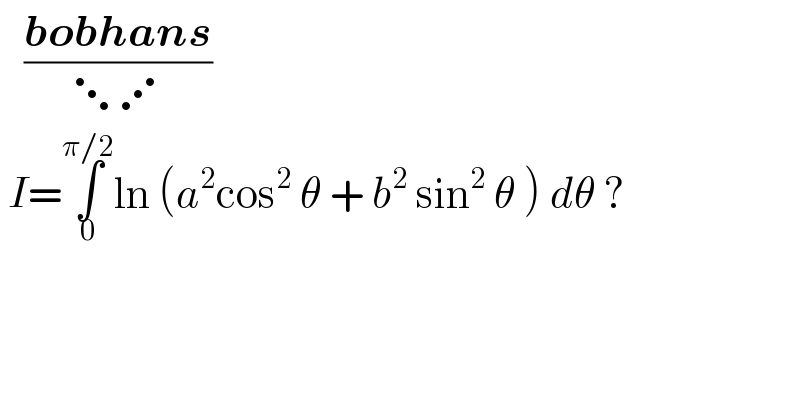
$$\:\:\:\frac{\boldsymbol{{bobhans}}}{\ddots\iddots} \\ $$$$\:{I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{ln}\:\left({a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\:+\:{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta\:\right)\:{d}\theta\:?\: \\ $$
Commented by john santu last updated on 17/Aug/20

$$\:\:\:\:\:\frac{\multimap{JS}\multimap}{\circledast} \\ $$$${I}\:=\pi\:\mathrm{ln}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$
Commented by bobhans last updated on 17/Aug/20
$${jooss}..{thank}\:{you}\:{all}\: \\ $$
Answered by Dwaipayan Shikari last updated on 16/Aug/20
![I=∫_0 ^(π/2) log(sin^2 θ+(a^2 /b^2 )cos^2 θ)+2logb=I(k)+πlogb I(k)=∫_0 ^(π/2) log(sin^2 θ+k^2 cos^2 θ) (k=(a/b)) I′(k)=∫_0 ^(π/2) ((2kcos^2 θ)/(sin^2 θ+k^2 cos^2 θ))dθ I^′ (k)=∫_0 ^(π/2) ((2k)/(tan^2 θ+k^2 ))dθ I^′ (k)=∫_0 ^(π/2) ((2k)/((tan^2 θ+k^2 )(tan^2 θ+1)))dt tanθ=t sec^2 θ=(dt/dθ) I^′ (k)=2k∫_0 ^∞ (1/(t^2 +k^2 ))−(1/(t^2 +1)) dt I′(k)=((2k)/(k^2 −1))∫_0 ^∞ (1/(t^2 +1))−(1/(t^2 +k^2 ))dt I′(k)=((2k)/(k^2 −1))[tan^(−1) t−(1/k)tan^(−1) (t/k)]_0 ^∞ I^′ (k)=((2k)/(k^2 −1)).((k−1)/k).(π/2)=(π/(k+1)) I(k)=∫(π/(k+1))=πlog(k+1)+C=∫_0 ^(π/2) log(sin^2 θ+k^2 cos^2 θ) If k=1 , πlog(2)+C=0, C=−πlog(2) I(k)=πlog(k+1)−πlog(2)=πlog(a+b)−πlog(2)−πlog(b) So Answer is I(k)+πlogb πlog(((a+b)/2))](https://www.tinkutara.com/question/Q108404.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{cos}^{\mathrm{2}} \theta\right)+\mathrm{2}{logb}={I}\left({k}\right)+\pi{logb} \\ $$$${I}\left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)\:\:\:\left({k}=\frac{{a}}{{b}}\right) \\ $$$${I}'\left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{kcos}^{\mathrm{2}} \theta}{{sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}{d}\theta \\ $$$${I}^{'} \left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{k}}{{tan}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} }{d}\theta \\ $$$${I}^{'} \left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{k}}{\left({tan}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} \right)\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tan}\theta={t}\:\:\:\:{sec}^{\mathrm{2}} \theta=\frac{{dt}}{{d}\theta} \\ $$$${I}^{'} \left({k}\right)=\mathrm{2}{k}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$$${I}'\left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{k}^{\mathrm{2}} }{dt} \\ $$$${I}'\left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}\left[{tan}^{−\mathrm{1}} {t}−\frac{\mathrm{1}}{{k}}{tan}^{−\mathrm{1}} \frac{{t}}{{k}}\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}^{'} \left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}.\frac{{k}−\mathrm{1}}{{k}}.\frac{\pi}{\mathrm{2}}=\frac{\pi}{{k}+\mathrm{1}} \\ $$$${I}\left({k}\right)=\int\frac{\pi}{{k}+\mathrm{1}}=\pi{log}\left({k}+\mathrm{1}\right)+{C}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right) \\ $$$${If}\:{k}=\mathrm{1}\:\:,\:\:\pi{log}\left(\mathrm{2}\right)+{C}=\mathrm{0},\:\:{C}=−\pi{log}\left(\mathrm{2}\right)\: \\ $$$${I}\left({k}\right)=\pi{log}\left({k}+\mathrm{1}\right)−\pi{log}\left(\mathrm{2}\right)=\pi{log}\left({a}+{b}\right)−\pi{log}\left(\mathrm{2}\right)−\pi{log}\left({b}\right) \\ $$$${So} \\ $$$${Answer}\:{is}\:\:\:\:\:{I}\left({k}\right)+\pi{logb} \\ $$$$\pi{log}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 16/Aug/20
![I=∫_0 ^(π/2) log(sin^2 θ+(a^2 /b^2 )cos^2 θ)+2logb=I(k)+πlogb I(k)=∫_0 ^(π/2) log(sin^2 θ+k^2 cos^2 θ) (k=(a/b)) I′(k)=∫_0 ^(π/2) ((2kcos^2 θ)/(sin^2 θ+k^2 cos^2 θ))dθ I^′ (k)=∫_0 ^(π/2) ((2k)/(tan^2 θ+k^2 ))dθ I^′ (k)=∫_0 ^(π/2) ((2k)/((tan^2 θ+k^2 )(tan^2 θ+1)))dt tanθ=t sec^2 θ=(dt/dθ) I^′ (k)=2k∫_0 ^∞ (1/(t^2 +k^2 ))−(1/(t^2 +1)) dt I′(k)=((2k)/(k^2 −1))∫_0 ^∞ (1/(t^2 +1))−(1/(t^2 +k^2 ))dt I′(k)=((2k)/(k^2 −1))[tan^(−1) t−(1/k)tan^(−1) (t/k)]_0 ^∞ I^′ (k)=((2k)/(k^2 −1)).((k−1)/k).(π/2)=(π/(k+1)) I(k)=∫(π/(k+1))=πlog(k+1)+C=∫_0 ^(π/2) log(sin^2 θ+k^2 cos^2 θ) If k=1 , πlog(2)+C=0, C=−πlog(2) I(k)=πlog(k+1)−πlog(2)=πlog(a+b)−πlog(2)−πlog(b) So Answer is I(k)+πlogb ♣πlog(((a+b)/2))...⇒∫_0 ^(π/2) {log(a^2 sin^2 (x) + b^2 cos^2 (x))}dx=πlog(((a+b)/2))♣ peace upon you. thank you very excellent.](https://www.tinkutara.com/question/Q108409.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{cos}^{\mathrm{2}} \theta\right)+\mathrm{2}{logb}={I}\left({k}\right)+\pi{logb} \\ $$$${I}\left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)\:\:\:\left({k}=\frac{{a}}{{b}}\right) \\ $$$${I}'\left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{kcos}^{\mathrm{2}} \theta}{{sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}{d}\theta \\ $$$${I}^{'} \left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{k}}{{tan}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} }{d}\theta \\ $$$${I}^{'} \left({k}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{k}}{\left({tan}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} \right)\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tan}\theta={t}\:\:\:\:{sec}^{\mathrm{2}} \theta=\frac{{dt}}{{d}\theta} \\ $$$${I}^{'} \left({k}\right)=\mathrm{2}{k}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$$${I}'\left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{k}^{\mathrm{2}} }{dt} \\ $$$${I}'\left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}\left[{tan}^{−\mathrm{1}} {t}−\frac{\mathrm{1}}{{k}}{tan}^{−\mathrm{1}} \frac{{t}}{{k}}\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}^{'} \left({k}\right)=\frac{\mathrm{2}{k}}{{k}^{\mathrm{2}} −\mathrm{1}}.\frac{{k}−\mathrm{1}}{{k}}.\frac{\pi}{\mathrm{2}}=\frac{\pi}{{k}+\mathrm{1}} \\ $$$${I}\left({k}\right)=\int\frac{\pi}{{k}+\mathrm{1}}=\pi{log}\left({k}+\mathrm{1}\right)+{C}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{2}} \theta+{k}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right) \\ $$$${If}\:{k}=\mathrm{1}\:\:,\:\:\pi{log}\left(\mathrm{2}\right)+{C}=\mathrm{0},\:\:{C}=−\pi{log}\left(\mathrm{2}\right)\: \\ $$$${I}\left({k}\right)=\pi{log}\left({k}+\mathrm{1}\right)−\pi{log}\left(\mathrm{2}\right)=\pi{log}\left({a}+{b}\right)−\pi{log}\left(\mathrm{2}\right)−\pi{log}\left({b}\right) \\ $$$${So} \\ $$$${Answer}\:{is}\:\:\:\:\:{I}\left({k}\right)+\pi{logb} \\ $$$$\clubsuit\pi{log}\left(\frac{{a}+{b}}{\mathrm{2}}\right)…\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{{log}\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} \left({x}\right)\:+\:{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \left({x}\right)\right)\right\}{dx}=\pi{log}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\clubsuit \\ $$$$ \\ $$$$\mathrm{peace}\:\mathrm{upon}\:\mathrm{you}.\:\mathrm{thank}\:\mathrm{you}\: \\ $$$$\mathrm{very}\:\mathrm{excellent}. \\ $$
Answered by mathmax by abdo last updated on 16/Aug/20

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}+\mathrm{b}^{\mathrm{2}} \frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\:\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left\{\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\:\mathrm{cos}\left(\mathrm{2}\theta\right)\right\}\mathrm{d}\theta\right. \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left\{\mathrm{1}+\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\:\mathrm{cos}\left(\mathrm{2}\theta\right)\right\}\mathrm{d}\theta\:\:\left(\mathrm{2}\theta\:=\mathrm{x}\right)\:\left(\alpha=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\alpha\:\mathrm{cosx}\right)\mathrm{dx}\:\mathrm{let}\:\mathrm{explicit}\:\mathrm{for}\:\mathrm{o}<\alpha<\mathrm{1} \\ $$$$\mathrm{f}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\alpha\:\mathrm{cosx}\right)\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\alpha\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosx}}{\mathrm{1}+\alpha\:\mathrm{cosx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\alpha}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}+\alpha\mathrm{cosx}\:−\mathrm{1}}{\mathrm{1}+\alpha\mathrm{cosx}}\mathrm{dx}\:=\frac{\pi}{\alpha}−\frac{\mathrm{1}}{\alpha}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\alpha\:\mathrm{cosx}} \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\alpha\mathrm{cosx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:+\alpha−\alpha\mathrm{t}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{1}−\alpha\right)\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}+\alpha}\:=\frac{\mathrm{2}}{\mathrm{1}−\alpha}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}} \\ $$$$=_{\mathrm{t}\:=\sqrt{\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}}\mathrm{u}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−\alpha}.\frac{\mathrm{1}−\alpha}{\mathrm{1}+\alpha}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{1}+\alpha}}{\:\sqrt{\mathrm{1}−\alpha}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}^{'} \left(\alpha\right)\:=\frac{\pi}{\alpha}−\frac{\pi}{\alpha\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\mathrm{f}\left(\alpha\right)\:=\pi\:\int_{\mathrm{1}} ^{\alpha} \:\frac{\mathrm{dt}}{\mathrm{t}}−\pi\:\int_{\mathrm{1}} ^{\alpha} \:\frac{\mathrm{dt}}{\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:+\mathrm{C}\:=\pi\mathrm{ln}\alpha\:−\pi\int_{\mathrm{1}} ^{\alpha} \:\frac{\mathrm{dt}}{\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:+\mathrm{C} \\ $$$$\mathrm{C}\:=\mathrm{f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{cosx}\right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{1}} ^{\alpha} \:\frac{\mathrm{dt}}{\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:=_{\mathrm{t}=\mathrm{sinz}} \:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\alpha} \:\:\frac{\mathrm{cosz}\:\mathrm{dz}}{\mathrm{sinz}\:\mathrm{cosz}}\:=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{arcsin}\alpha} \:\frac{\mathrm{dz}}{\mathrm{sinz}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{z}}{\mathrm{2}}\right)=\mathrm{m}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{tan}\left(\frac{\mathrm{arcsin}\alpha}{\mathrm{2}}\right)} \:\:\frac{\mathrm{2dm}}{\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\frac{\mathrm{2m}}{\mathrm{1}+\mathrm{m}^{\mathrm{2}} }}\:=\int_{\mathrm{1}} ^{\mathrm{tan}\left(\frac{\mathrm{arcsin}\alpha}{\mathrm{2}}\right)} \:\frac{\mathrm{dm}}{\mathrm{m}} \\ $$$$=\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{arcsin}\alpha}{\mathrm{2}}\right)\mid\:\Rightarrow\mathrm{f}\left(\alpha\right)\:=\pi\mathrm{ln}\left(\alpha\right)−\pi\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{arcsin}\alpha}{\mathrm{2}}\right)\mid\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}\left(\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\right) \\ $$
Commented by mathmax by abdo last updated on 16/Aug/20
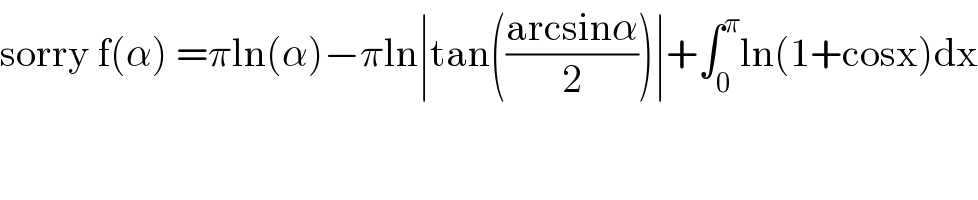
$$\mathrm{sorry}\:\mathrm{f}\left(\alpha\right)\:=\pi\mathrm{ln}\left(\alpha\right)−\pi\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{arcsin}\alpha}{\mathrm{2}}\right)\mid+\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{1}+\mathrm{cosx}\right)\mathrm{dx} \\ $$
