Question Number 108444 by bobhans last updated on 17/Aug/20
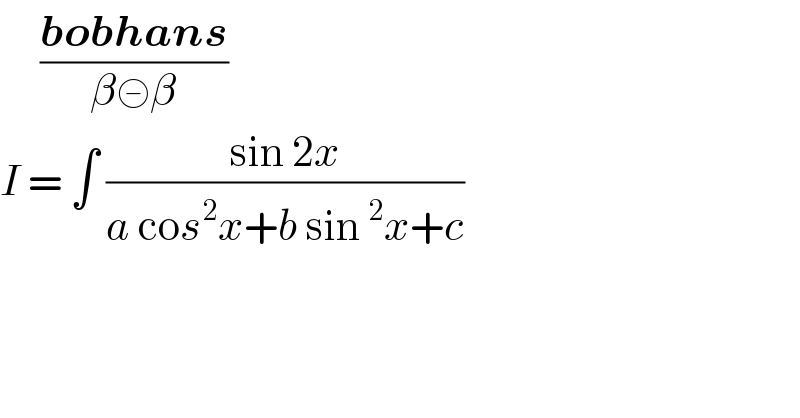
$$\:\:\:\:\:\frac{\boldsymbol{{bobhans}}}{\beta\circleddash\beta} \\ $$$${I}\:=\:\int\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{{a}\:\mathrm{co}{s}^{\mathrm{2}} {x}+{b}\:\mathrm{sin}\:^{\mathrm{2}} {x}+{c}} \\ $$
Answered by john santu last updated on 17/Aug/20
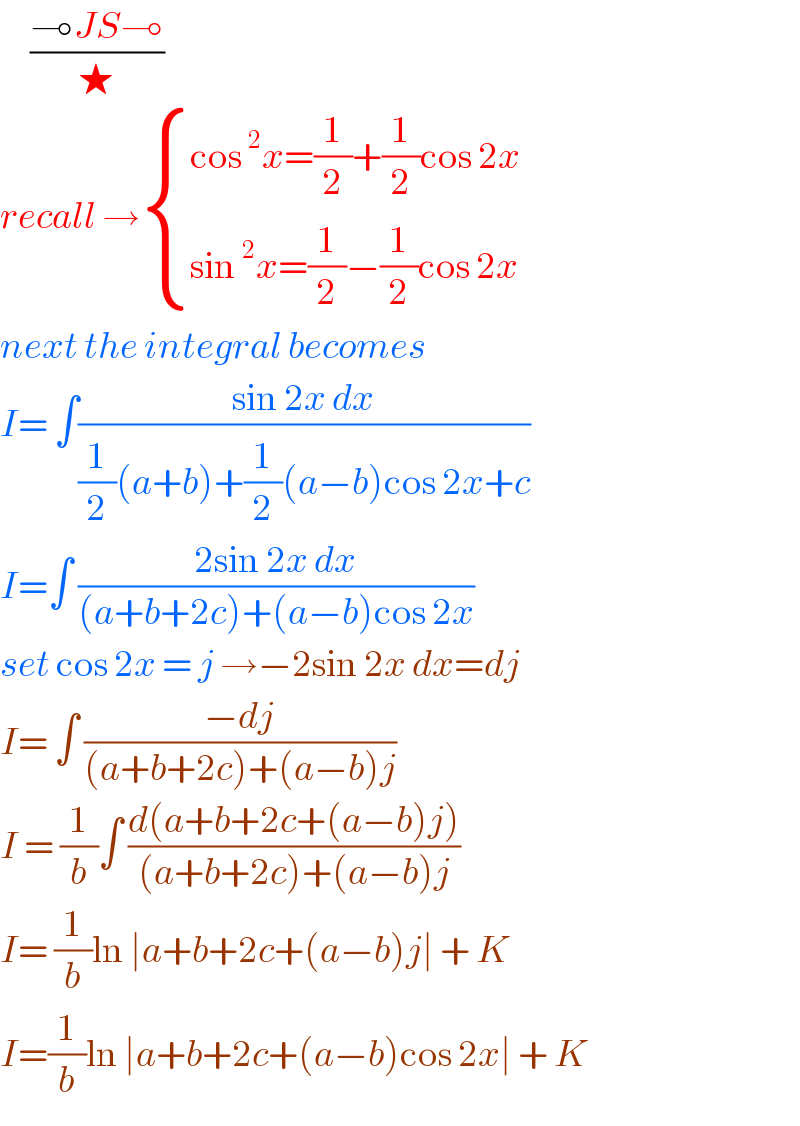
$$\:\:\:\:\:\frac{\multimap{JS}\multimap}{\bigstar} \\ $$$${recall}\:\rightarrow\begin{cases}{\mathrm{cos}\:^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}}\\{\mathrm{sin}\:^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}}\end{cases} \\ $$$${next}\:{the}\:{integral}\:{becomes} \\ $$$${I}=\:\int\frac{\mathrm{sin}\:\mathrm{2}{x}\:{dx}}{\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{b}\right)\mathrm{cos}\:\mathrm{2}{x}+{c}} \\ $$$${I}=\int\:\frac{\mathrm{2sin}\:\mathrm{2}{x}\:{dx}}{\left({a}+{b}+\mathrm{2}{c}\right)+\left({a}−{b}\right)\mathrm{cos}\:\mathrm{2}{x}} \\ $$$${set}\:\mathrm{cos}\:\mathrm{2}{x}\:=\:{j}\:\rightarrow−\mathrm{2sin}\:\mathrm{2}{x}\:{dx}={dj} \\ $$$${I}=\:\int\:\frac{−{dj}}{\left({a}+{b}+\mathrm{2}{c}\right)+\left({a}−{b}\right){j}} \\ $$$${I}\:=\:\frac{\mathrm{1}}{{b}}\int\:\frac{{d}\left({a}+{b}+\mathrm{2}{c}+\left({a}−{b}\right){j}\right)}{\left({a}+{b}+\mathrm{2}{c}\right)+\left({a}−{b}\right){j}} \\ $$$${I}=\:\frac{\mathrm{1}}{{b}}\mathrm{ln}\:\mid{a}+{b}+\mathrm{2}{c}+\left({a}−{b}\right){j}\mid\:+\:{K} \\ $$$${I}=\frac{\mathrm{1}}{{b}}\mathrm{ln}\:\mid{a}+{b}+\mathrm{2}{c}+\left({a}−{b}\right)\mathrm{cos}\:\mathrm{2}{x}\mid\:+\:{K}\: \\ $$
