Menu Close

bobhans-lim-x-0-1-sin-4x-1-3-cos-2x-x-tan-x-

Tinku Tara 0 Comments
Pin




Question Number 106842 by bobhans last updated on 07/Aug/20
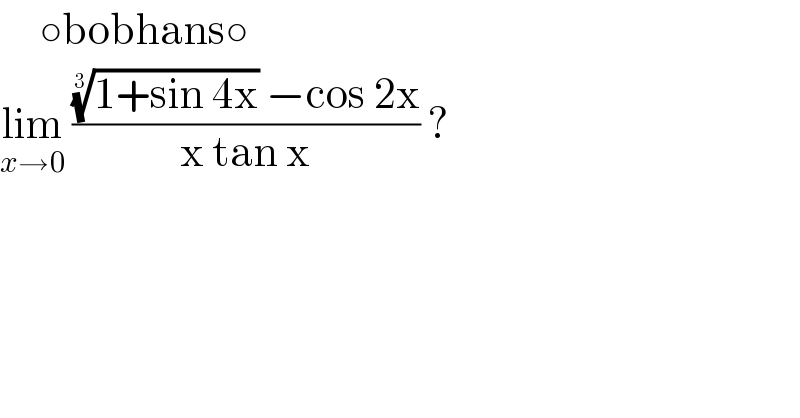
○bobhans○ lim_(x→0) ((((1+sin 4x))^(1/3) −cos 2x)/(x tan x)) ?
$$\:\:\:\:\:\circ\mathrm{bobhans}\circ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{4x}}\:−\mathrm{cos}\:\mathrm{2x}}{\mathrm{x}\:\mathrm{tan}\:\mathrm{x}}\:? \\ $$
Commented by bemath last updated on 07/Aug/20
the limit is DNE
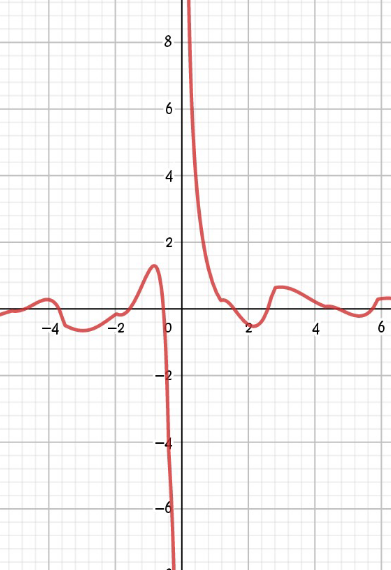
$$\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{DNE}\: \\ $$
Commented by bemath last updated on 07/Aug/20
Commented by bemath last updated on 07/Aug/20
lim_(x→0^− ) f(x)≠lim_(x→0^+ ) f(x)
$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}f}\left(\mathrm{x}\right)\neq\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}f}\left(\mathrm{x}\right) \\ $$
Commented by 1549442205PVT last updated on 07/Aug/20
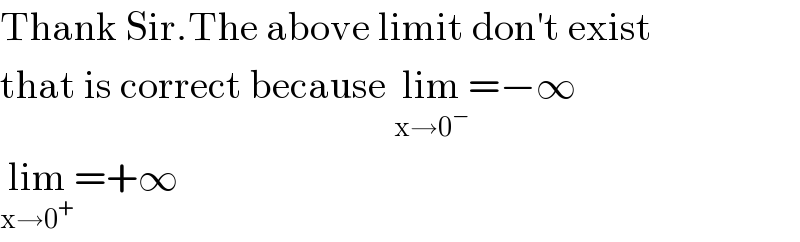
Thank Sir.The above limit don′t exist that is correct because lim_(x→0^− ) =−∞ lim_(x→0^+ ) =+∞
$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{The}\:\mathrm{above}\:\mathrm{limit}\:\mathrm{don}'\mathrm{t}\:\mathrm{exist} \\ $$$$\mathrm{that}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{because}\:\underset{\mathrm{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}=−\infty \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}=+\infty \\ $$
Commented by bobhans last updated on 07/Aug/20
yes..limit DNE
$$\mathrm{yes}..\mathrm{limit}\:\mathrm{DNE} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Aug/20
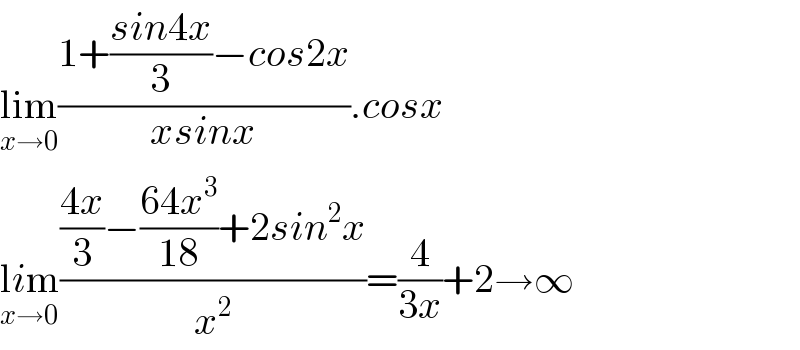
lim_(x→0) ((1+((sin4x)/3)−cos2x)/(xsinx)).cosx lim_(x→0) ((((4x)/3)−((64x^3 )/(18))+2sin^2 x)/x^2 )=(4/(3x))+2→∞
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\frac{{sin}\mathrm{4}{x}}{\mathrm{3}}−{cos}\mathrm{2}{x}}{{xsinx}}.{cosx} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{l}{i}\mathrm{m}}\frac{\frac{\mathrm{4}{x}}{\mathrm{3}}−\frac{\mathrm{64}{x}^{\mathrm{3}} }{\mathrm{18}}+\mathrm{2}{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{3}{x}}+\mathrm{2}\rightarrow\infty \\ $$
Commented by Dwaipayan Shikari last updated on 07/Aug/20
Limit doesn′t exist
$${Limit}\:{doesn}'{t}\:{exist} \\ $$
Answered by 1549442205PVT last updated on 07/Aug/20
Multiplying both the numerator and denominator by the conjugate expression of numerator: (applying the identity:(a−b)(a^2 +ab+b^2 )=a^3 −b^3 ) ((((1+sin 4x))^(1/3) −cos 2x)/(x tan x)) =((1+sin4x−cos^3 2x)/(xtanx(^3 (√((1+sin4x)^2 )) +cos2x^3 (√(1+sin4x )) +cos^2 2x))) =((1+sin4x−cos^3 2x)/(xtanx(^3 (√((1+sin4x)^2 )) +cos2x^3 (√(1+sin4x )) +cos^2 2x))) Hence,lim_(x→0) ((((1+sin 4x))^(1/3) −cos 2x)/(x tan x))= lm_(x→0) ((1+sin 4x −cos^3 2x)/(x tan x))×lim_(x→0) (1/(^3 (√((1+sin4x)^2 )) +cos2x^3 (√(1+sin4x )) +cos^2 2x)) lim_(x→0) ((1+sin4x−cos^3 2x)/(xtanx)) = _(L′Hopital) lim _(x→0) ((4cos4x+6cos^2 2xsin2x)/(tanx+x(1+tan^2 x))) ×(1/3) =(4/0)×(1/3)=∞
$$\mathrm{Multiplying}\:\mathrm{both}\:\mathrm{the}\:\mathrm{numerator}\:\mathrm{and}\:\mathrm{denominator} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{conjugate}\:\mathrm{expression}\:\mathrm{of}\:\mathrm{numerator}: \\ $$$$\left(\mathrm{applying}\:\mathrm{the}\:\mathrm{identity}:\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right)=\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} \right) \\ $$$$\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{4x}}\:−\mathrm{cos}\:\mathrm{2x}}{\mathrm{x}\:\mathrm{tan}\:\mathrm{x}}\:=\frac{\mathrm{1}+\mathrm{sin4x}−\mathrm{cos}^{\mathrm{3}} \mathrm{2x}}{\mathrm{xtanx}\left(\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{sin4x}\right)^{\mathrm{2}} }\:+\mathrm{cos2x}\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin4x}\:}\:+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}\right)} \\ $$$$=\frac{\mathrm{1}+\mathrm{sin4x}−\mathrm{cos}^{\mathrm{3}} \mathrm{2x}}{\mathrm{xtanx}\left(\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{sin4x}\right)^{\mathrm{2}} }\:+\mathrm{cos2x}\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin4x}\:}\:+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}\right)} \\ $$$$\mathrm{Hence},\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{4x}}\:−\mathrm{cos}\:\mathrm{2x}}{\mathrm{x}\:\mathrm{tan}\:\mathrm{x}}= \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lm}}\:\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{4x}\:−\mathrm{cos}\:^{\mathrm{3}} \mathrm{2x}}{\mathrm{x}\:\mathrm{tan}\:\mathrm{x}}×\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{sin4x}\right)^{\mathrm{2}} }\:+\mathrm{cos2x}\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin4x}\:}\:+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{sin4x}−\mathrm{cos}^{\mathrm{3}} \mathrm{2x}}{\mathrm{xtanx}}\:\:\underset{\mathrm{L}'\mathrm{Hopital}} {\:\:=\:\:}\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}\:}\frac{\mathrm{4cos4x}+\mathrm{6cos}^{\mathrm{2}} \mathrm{2xsin2x}}{\mathrm{tanx}+\mathrm{x}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}\:×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{0}}×\frac{\mathrm{1}}{\mathrm{3}}=\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *