Question Number 108891 by bobhans last updated on 20/Aug/20
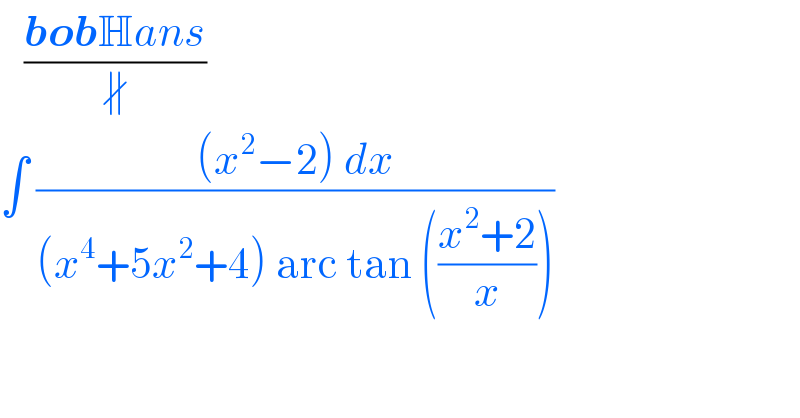
$$\:\:\:\frac{\boldsymbol{{bob}}\mathbb{H}{ans}}{\nparallel} \\ $$$$\int\:\frac{\left({x}^{\mathrm{2}} −\mathrm{2}\right)\:{dx}}{\left({x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}\right)\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right)} \\ $$
Answered by bemath last updated on 20/Aug/20

$$\:\:\:\frac{\wedge\mathcal{B}{e}\mathcal{M}{ath}\wedge}{\iddots\ddots\iddots\ddots\iddots\ddots} \\ $$$${let}\:{w}\:=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right) \\ $$$$\frac{{dw}}{{dx}}\:=\:\frac{{d}\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right)}{\mathrm{1}+\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right)^{\mathrm{2}} }\:=\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}\:.\left(\mathrm{1}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right) \\ $$$$=\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}\:.\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} }\:=\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$${I}\:=\:\int\:\frac{{dw}}{{w}}\:=\:\mathrm{ln}\:\mid{w}\mid\:+\:{c}\:=\:\mathrm{ln}\:\mid\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right)\mid\:+\:{c} \\ $$
