Menu Close

bonjour-calculer-la-limite-suivante-en-utilisant-les-developpements-limites-lim-x-0-1-x-2-1-sin-2-x-

Tinku Tara 0 Comments
Pin




Question Number 157647 by wendjudi last updated on 26/Oct/21
bonjour ,calculer la limite suivante en utilisant les developpements limites: lim_(x→0) ((1/x^2 ) − (1/(sin^2 x))).
$${bonjour}\:,{calculer}\:{la}\:{limite}\:{suivante}\:{en}\:{utilisant}\:{les}\:{developpements}\:{limites}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\right). \\ $$
Commented by cortano last updated on 26/Oct/21
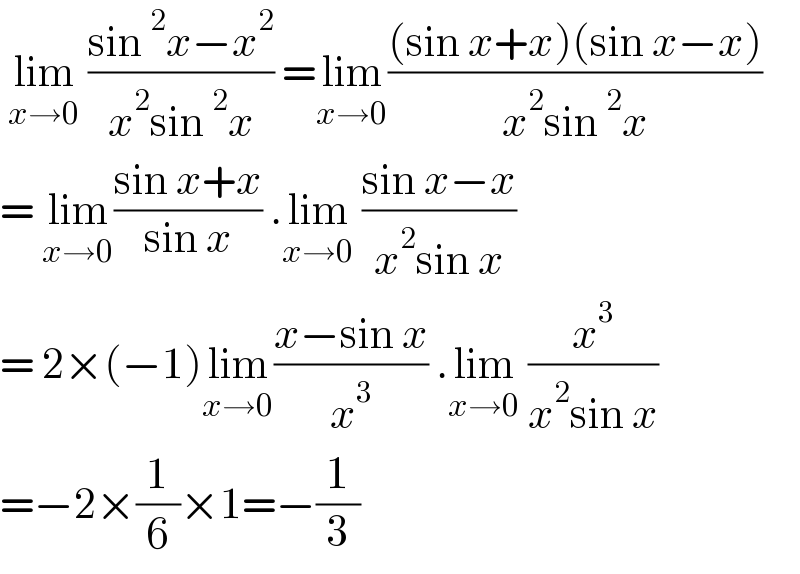
lim_(x→0) ((sin^2 x−x^2 )/(x^2 sin^2 x)) =lim_(x→0) (((sin x+x)(sin x−x))/(x^2 sin^2 x)) = lim_(x→0) ((sin x+x)/(sin x)) .lim_(x→0) ((sin x−x)/(x^2 sin x)) = 2×(−1)lim_(x→0) ((x−sin x)/x^3 ) .lim_(x→0) (x^3 /(x^2 sin x)) =−2×(1/6)×1=−(1/3)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}}\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{sin}\:{x}+{x}\right)\left(\mathrm{sin}\:{x}−{x}\right)}{{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}+{x}}{\mathrm{sin}\:{x}}\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−{x}}{{x}^{\mathrm{2}} \mathrm{sin}\:{x}} \\ $$$$=\:\mathrm{2}×\left(−\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} \mathrm{sin}\:{x}} \\ $$$$=−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by wendjudi last updated on 26/Oct/21
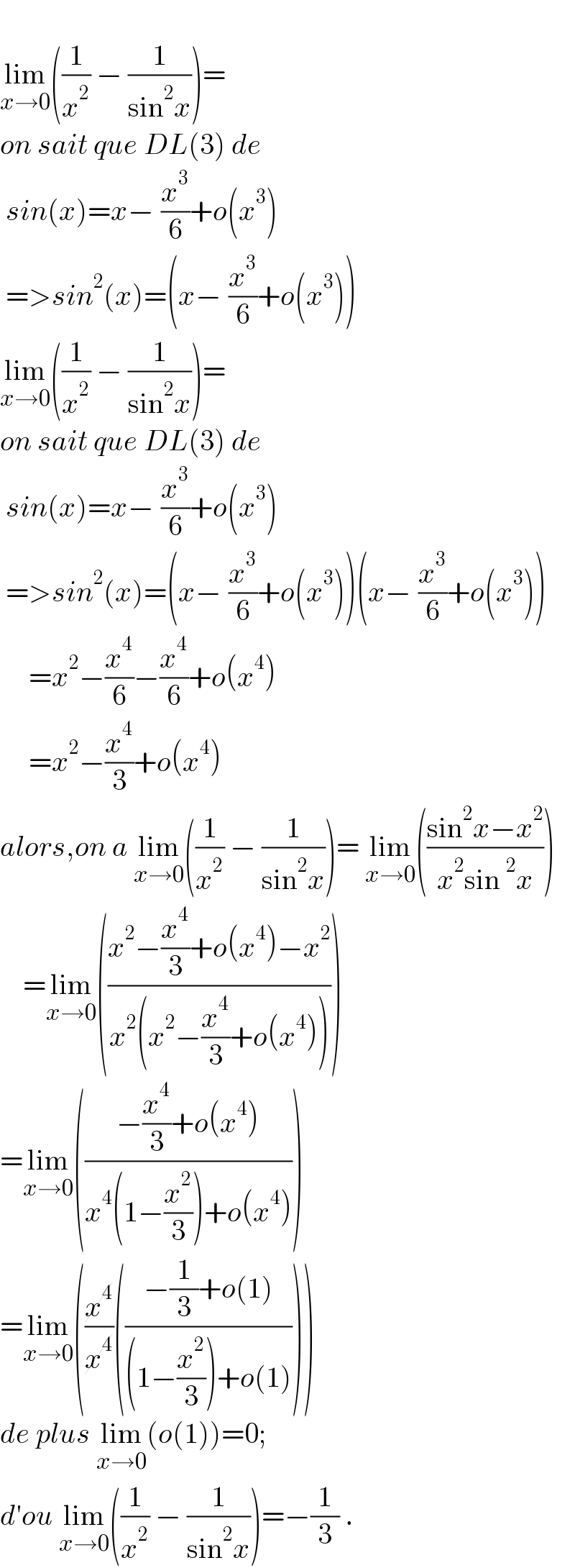
lim_(x→0) ((1/x^2 ) − (1/(sin^2 x)))= on sait que DL(3) de sin(x)=x−_ (x^3 /6)+o(x_ ^3 ) =>sin^2 (x)=(x−_ (x^3 /6)+o(x_ ^3 )) lim_(x→0) ((1/x^2 ) − (1/(sin^2 x)))= on sait que DL(3) de sin(x)=x−_ (x^3 /6)+o(x_ ^3 ) =>sin^2 (x)=(x−_ (x^3 /6)+o(x_ ^3 ))(x−_ (x^3 /6)+o(x_ ^3 )) =x^2 −(x^4 /6)−(x^4 /6)+o(x^4 ) =x^2 −(x^4 /3)+o(x^4 ) alors,on a lim_(x→0) ((1/x^2 ) − (1/(sin^2 x)))= lim_(x→0) (((sin^2 x−x^2 )/(x^2 sin^2 x))) =lim_(x→0) (((x^2 −(x^4 /3)+o(x^4 )−x^2 )/(x^2 (x^2 −(x^4 /3)+o(x^4 ))))) =lim_(x→0) (((−(x^4 /3)+o(x^4 ))/(x^4 (1−(x^2 /3))+o(x^4 )))) =lim_(x→0) ((x^4 /x^4 )(((−(1/3)+o(1))/((1−(x^2 /3))+o(1))))) de plus lim_(x→0) (o(1))=0; d′ou lim_(x→0) ((1/x^2 ) − (1/(sin^2 x)))=−(1/3) .
$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\right)=\: \\ $$$${on}\:{sait}\:{que}\:{DL}\left(\mathrm{3}\right)\:{de} \\ $$$$\:{sin}\left({x}\right)={x}−_{} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}_{} ^{\mathrm{3}} \right) \\ $$$$\:=>{sin}^{\mathrm{2}} \left({x}\right)=\left({x}−_{} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}_{} ^{\mathrm{3}} \right)\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\right)=\: \\ $$$${on}\:{sait}\:{que}\:{DL}\left(\mathrm{3}\right)\:{de} \\ $$$$\:{sin}\left({x}\right)={x}−_{} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}_{} ^{\mathrm{3}} \right) \\ $$$$\:=>{sin}^{\mathrm{2}} \left({x}\right)=\left({x}−_{} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}_{} ^{\mathrm{3}} \right)\right)\left({x}−_{} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}_{} ^{\mathrm{3}} \right)\right) \\ $$$$\:\:\:\:\:={x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{6}}−\frac{{x}^{\mathrm{4}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:\:={x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$${alors},{on}\:{a}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\right)=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}^{\mathrm{2}} {x}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}}\right) \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+{o}\left({x}^{\mathrm{4}} \right)−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+{o}\left({x}^{\mathrm{4}} \right)\right)}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+{o}\left({x}^{\mathrm{4}} \right)}{{x}^{\mathrm{4}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)+{o}\left({x}^{\mathrm{4}} \right)}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\cancel{{x}^{\mathrm{4}} }}{\cancel{{x}^{\mathrm{4}} }}\left(\frac{−\frac{\mathrm{1}}{\mathrm{3}}+{o}\left(\mathrm{1}\right)}{\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)+{o}\left(\mathrm{1}\right)}\right)\right) \\ $$$${de}\:{plus}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({o}\left(\mathrm{1}\right)\right)=\mathrm{0}; \\ $$$${d}'{ou}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\right)=−\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$
Commented by cortano last updated on 26/Oct/21
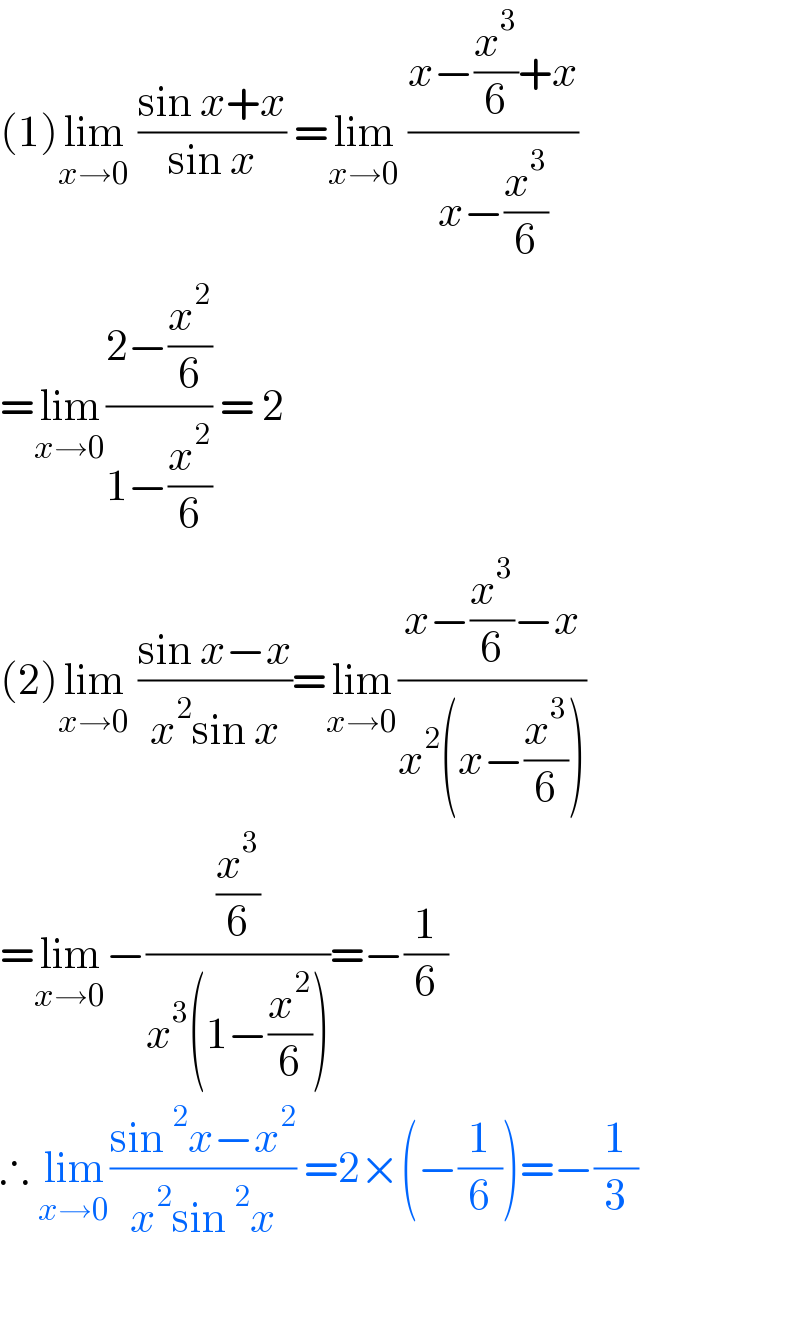
(1)lim_(x→0) ((sin x+x)/(sin x)) =lim_(x→0) ((x−(x^3 /6)+x)/(x−(x^3 /6))) =lim_(x→0) ((2−(x^2 /6))/(1−(x^2 /6))) = 2 (2)lim_(x→0) ((sin x−x)/(x^2 sin x))=lim_(x→0) ((x−(x^3 /6)−x)/(x^2 (x−(x^3 /6)))) =lim_(x→0) −((x^3 /6)/(x^3 (1−(x^2 /6))))=−(1/6) ∴ lim_(x→0) ((sin^2 x−x^2 )/(x^2 sin^2 x)) =2×(−(1/6))=−(1/3)
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}+{x}}{\mathrm{sin}\:{x}}\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{x}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−{x}}{{x}^{\mathrm{2}} \mathrm{sin}\:{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−{x}}{{x}^{\mathrm{2}} \left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}}\:=\mathrm{2}×\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *