Question Number 54966 by Tawa1 last updated on 15/Feb/19
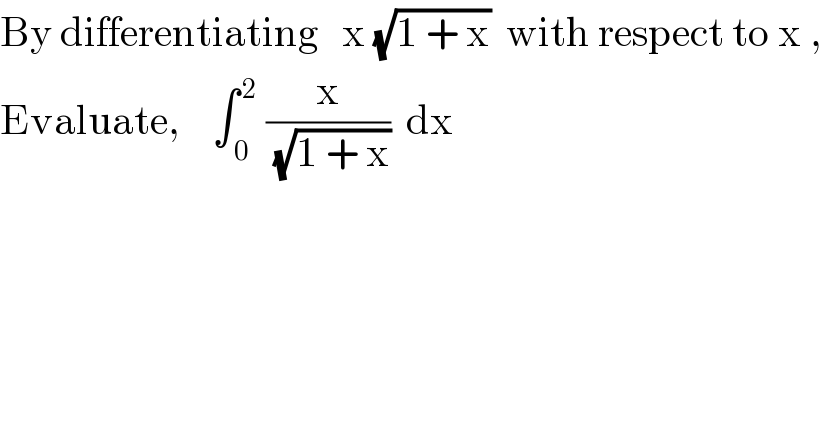
$$\mathrm{By}\:\mathrm{differentiating}\:\:\:\mathrm{x}\:\sqrt{\mathrm{1}\:+\:\mathrm{x}}\:\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{x}\:, \\ $$$$\mathrm{Evaluate},\:\:\:\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{x}}}\:\:\mathrm{dx} \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
![we have (x(√(1+x)))^′ =(√(1+x)) +(x/(2(√(1+x)))) ⇒x(√(1+x))= ∫(√(1+x)) +∫ (x/(2(√(1+x))))dx ⇒ ∫ ((xdx)/(2(√(1+x)))) =x(√(1+x))−∫ (√(1+x))dx +c ⇒ ∫_0 ^2 ((xdx)/(2(√(1+x)))) dx =[x(√(1+x))]_0 ^2 −∫_0 ^2 (√(1+x))dx =2(√3)−∫_0 ^2 (√(1+x))dx but ∫_0 ^2 (√(1+x))dx =∫_0 ^2 (1+x)^(1/2) dx =[(2/3)(1+x)^(3/2) ]_0 ^2 =(2/3)( 3^(3/2) −1) ⇒ I =2(√3)−(2/3)( (√(27))−1) =2(√3)−(2/3)(3(√3)−1) =2(√3)−2(√3) +(2/3) ⇒I=(2/3) .](https://www.tinkutara.com/question/Q55092.png)
$${we}\:{have}\:\left({x}\sqrt{\mathrm{1}+{x}}\right)^{'} =\sqrt{\mathrm{1}+{x}}\:+\frac{{x}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\:\Rightarrow{x}\sqrt{\mathrm{1}+{x}}=\:\int\sqrt{\mathrm{1}+{x}}\:+\int\:\frac{{x}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}{dx}\:\Rightarrow \\ $$$$\int\:\:\frac{{xdx}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\:={x}\sqrt{\mathrm{1}+{x}}−\int\:\sqrt{\mathrm{1}+{x}}{dx}\:+{c}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{xdx}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\:{dx}\:=\left[{x}\sqrt{\mathrm{1}+{x}}\right]_{\mathrm{0}} ^{\mathrm{2}} \:−\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{1}+{x}}{dx}\:=\mathrm{2}\sqrt{\mathrm{3}}−\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{1}+{x}}{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{1}+{x}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}\:=\left[\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{2}} \:=\frac{\mathrm{2}}{\mathrm{3}}\left(\:\mathrm{3}^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\mathrm{1}\right)\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\:\sqrt{\mathrm{27}}−\mathrm{1}\right)\:=\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)\:=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{I}=\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
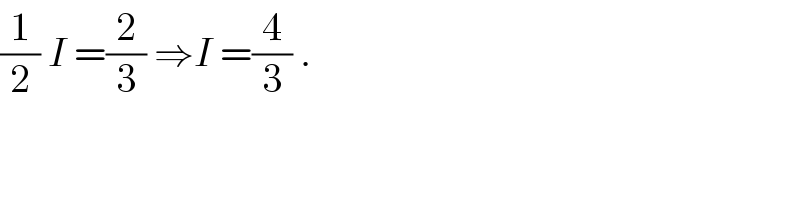
$$\frac{\mathrm{1}}{\mathrm{2}}\:{I}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{I}\:=\frac{\mathrm{4}}{\mathrm{3}}\:. \\ $$
Commented by Tawa1 last updated on 17/Feb/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 15/Feb/19
![((d(x(√(1+x))))/dx)=(x/(2(√(1+x))))+(√(1+x)) I_1 = ∫_( 0) ^( 2) (x/( (√(1 + x)))) dx I_2 = ∫_( 0) ^( 2) (√(1+x)) dx=(2/3)[(1+x)^(3/2) ]_0 ^2 =(2/3)(3(√3)−1)=2(√3)−(2/3) I=(1/2)I_1 +I_2 = ∫_( 0) ^( 2) ((x/(2(√(1 + x))))+(√(1+x))) dx=[x(√(1+x))]_0 ^2 =2(√3) ⇒I_1 =∫_( 0) ^( 2) (x/( (√(1 + x)))) dx=2(I_1 −I_2 )=2{2(√3)−(2(√3)−(2/3))}=(4/3)](https://www.tinkutara.com/question/Q54978.png)
$$\frac{{d}\left({x}\sqrt{\mathrm{1}+{x}}\right)}{{dx}}=\frac{{x}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}+\sqrt{\mathrm{1}+{x}} \\ $$$${I}_{\mathrm{1}} =\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{x}}}\:\:\mathrm{dx} \\ $$$${I}_{\mathrm{2}} =\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\sqrt{\mathrm{1}+{x}}\:\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\left[\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\left(\frac{\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{1}\:+\:\mathrm{x}}}+\sqrt{\mathrm{1}+{x}}\right)\:\mathrm{dx}=\left[{x}\sqrt{\mathrm{1}+{x}}\right]_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{I}_{\mathrm{1}} =\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{x}}}\:\mathrm{dx}=\mathrm{2}\left({I}_{\mathrm{1}} −{I}_{\mathrm{2}} \right)=\mathrm{2}\left\{\mathrm{2}\sqrt{\mathrm{3}}−\left(\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\right)\right\}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by Tawa1 last updated on 16/Feb/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
