Question Number 94354 by M±th+et+s last updated on 18/May/20
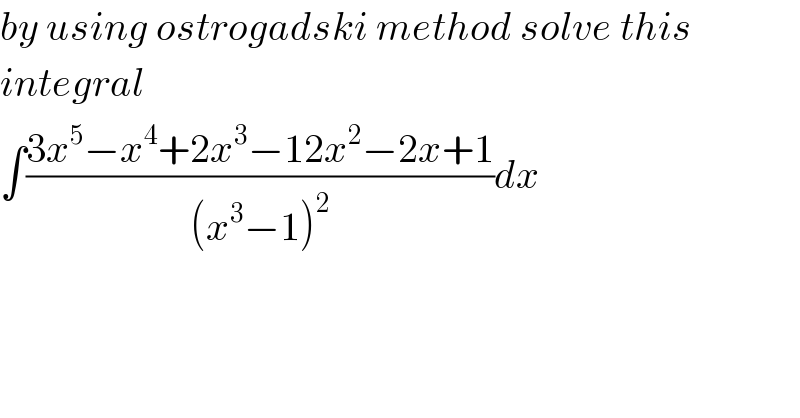
$${by}\:{using}\:{ostrogadski}\:{method}\:{solve}\:{this} \\ $$$${integral} \\ $$$$\int\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by MJS last updated on 18/May/20
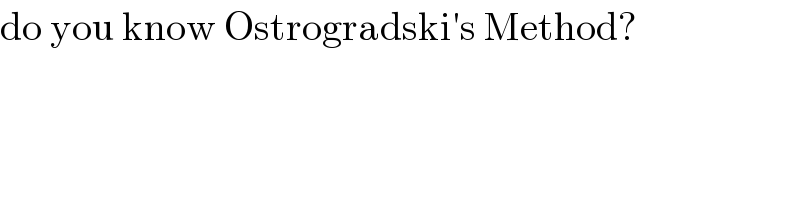
$$\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}? \\ $$
Commented by i jagooll last updated on 18/May/20
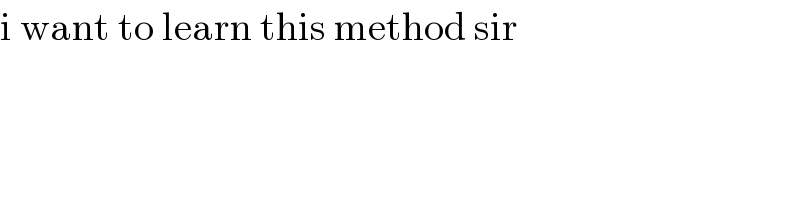
$$\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{this}\:\mathrm{method}\:\mathrm{sir} \\ $$
Commented by M±th+et+s last updated on 18/May/20
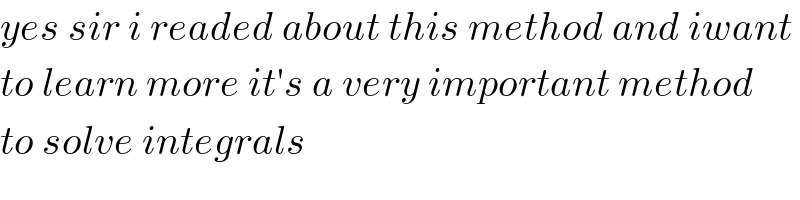
$${yes}\:{sir}\:{i}\:{readed}\:{about}\:{this}\:{method}\:{and}\:{iwant} \\ $$$${to}\:{learn}\:{more}\:{it}'{s}\:{a}\:{very}\:{important}\:{method} \\ $$$${to}\:{solve}\:{integrals} \\ $$
Answered by MJS last updated on 18/May/20
![we have p(x), q(x) are polynomes degree (p(x)) < degree (q(x)) ((p(x))/(q(x))) is a cancelled fraction ∫((p(x))/(q(x)))dx=((p_1 (x))/(q_1 (x)))+∫((p_2 (x))/(q_2 (x)))dx q_1 (x)=gcd (q(x), q′(x)); q_2 (x)=((q(x))/(q_1 (x))) now we differentiate both sides to get the constant factors ((p(x))/(q(x)))=(d/dx)[((p_1 (x))/(q_1 (x)))]+((p_2 (x))/(q_2 (x))) all we have to know is this: degree (p_i (x)) < degree (q_i (x)) in above case p(x)=3x^5 −x^4 +2x^3 −12x^2 −2x+1 q(x)=(x^3 −1)^2 q_1 (x)=q_2 (x)=x^3 −1 ((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))= =(d/dx)[((ax^2 +bx+c)/(x^3 −1))]+((dx^2 +ex+f)/(x^3 −1)) solve this for the constsnt factors a, ..., f ⇒ a=1, b=−1, c=3, d=3, e=0, f=0 ⇒ ∫((3x^5 −x^4 +2x^3 −12x^2 −2x+1)/((x^3 −1)^2 ))dx= =((x^2 −x+3)/(x^3 −1))+3∫(x^2 /(x^3 −1))dx and now it′s easy](https://www.tinkutara.com/question/Q94372.png)
$$\mathrm{we}\:\mathrm{have}\:{p}\left({x}\right),\:{q}\left({x}\right)\:\mathrm{are}\:\mathrm{polynomes} \\ $$$$\mathrm{degree}\:\left({p}\left({x}\right)\right)\:<\:\mathrm{degree}\:\left({q}\left({x}\right)\right) \\ $$$$\frac{{p}\left({x}\right)}{{q}\left({x}\right)}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cancelled}\:\mathrm{fraction} \\ $$$$\int\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}=\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcd}\:\left({q}\left({x}\right),\:{q}'\left({x}\right)\right);\:{q}_{\mathrm{2}} \left({x}\right)=\frac{{q}\left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{differentiate}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{constant}\:\mathrm{factors} \\ $$$$\frac{{p}\left({x}\right)}{{q}\left({x}\right)}=\frac{{d}}{{dx}}\left[\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}\right]+\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\mathrm{all}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{know}\:\mathrm{is}\:\mathrm{this}: \\ $$$$\mathrm{degree}\:\left({p}_{{i}} \left({x}\right)\right)\:<\:\mathrm{degree}\:\left({q}_{{i}} \left({x}\right)\right) \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{above}\:\mathrm{case} \\ $$$${p}\left({x}\right)=\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$${q}\left({x}\right)=\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$${q}_{\mathrm{1}} \left({x}\right)={q}_{\mathrm{2}} \left({x}\right)={x}^{\mathrm{3}} −\mathrm{1} \\ $$$$\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:=\frac{{d}}{{dx}}\left[\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{x}^{\mathrm{3}} −\mathrm{1}}\right]+\frac{{dx}^{\mathrm{2}} +{ex}+{f}}{{x}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:\mathrm{the}\:\mathrm{constsnt}\:\mathrm{factors}\:{a},\:…,\:{f} \\ $$$$\Rightarrow \\ $$$${a}=\mathrm{1},\:{b}=−\mathrm{1},\:{c}=\mathrm{3},\:{d}=\mathrm{3},\:{e}=\mathrm{0},\:{f}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\int\frac{\mathrm{3}{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} −\mathrm{1}}+\mathrm{3}\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{1}}{dx} \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$
Commented by M±th+et+s last updated on 18/May/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by I want to learn more last updated on 09/Jun/20

$$\mathrm{wow}.\:\mathrm{Thanks}\:\mathrm{sir} \\ $$
