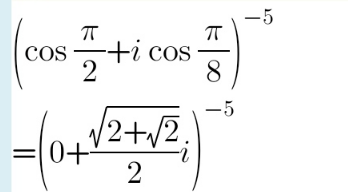by-ussing-demover-find-cos-pi-2-i-cos-pi-8-5-

Question Number 177280 by mokys last updated on 02/Oct/22

b y u s s i n g d e m o v e r f i n d

{(c o s \frac{π}{2} + i c o s \frac{π}{8})}^{- 5}

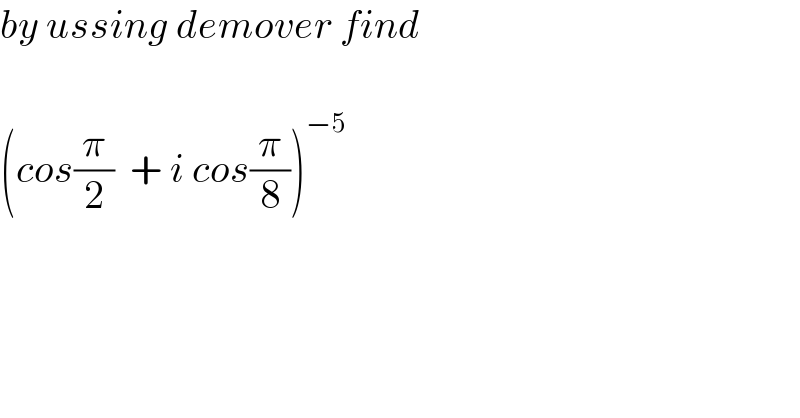
Commented by Frix last updated on 03/Oct/22

\cos \frac{π}{2} = 0

\cos \frac{π}{8} = \frac{\sqrt{2 + \sqrt{2}}}{2}

\Rightarrow answer is 8 (4 - 3 \sqrt{2}) \sqrt{2 - \sqrt{2}} i

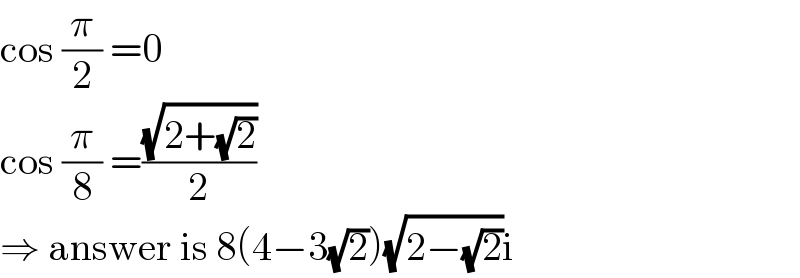
Answered by Ar Brandon last updated on 03/Oct/22

{(\cos \frac{π}{2} + i \cos \frac{π}{8})}^{- 5} = {(i \sin \frac{3 π}{8})}^{- 5} = \frac{1}{i \sin^{5} (\frac{3 π}{8})}

\cos (\frac{3 π}{4}) = 1 - {2 \sin}^{2} (\frac{3 π}{8}) \Rightarrow - \frac{\sqrt{2}}{2} = 1 - {2 \sin}^{2} (\frac{3 π}{8})

\Rightarrow \sin (\frac{3 π}{8}) = \pm \frac{\sqrt{2 + \sqrt{2}}}{2} = \frac{\sqrt{2 + \sqrt{2}}}{2} (\sin ϑ > 0 : 0 < ϑ < π)

{(\cos \frac{π}{2} + i \cos \frac{π}{8})}^{- 5} = - \frac{2^{5}}{\sqrt{{(2 + \sqrt{2})}^{5}}} i

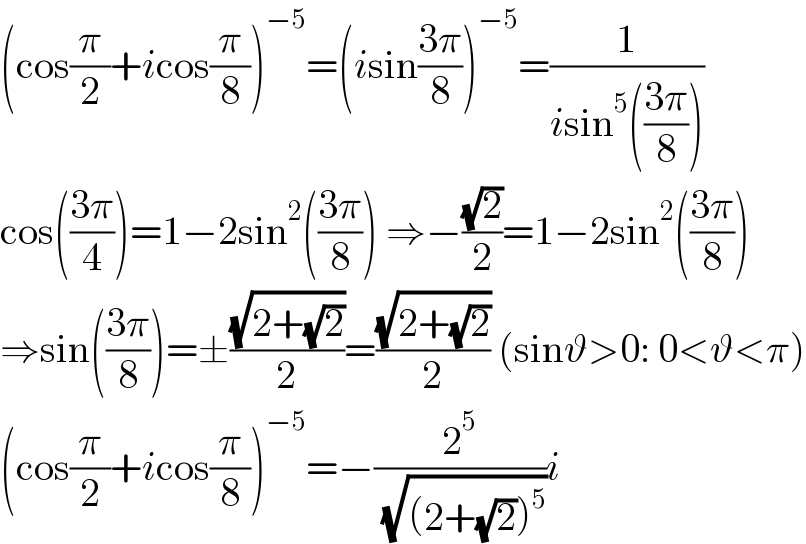
Commented by puissant last updated on 04/Oct/22

.

Answered by mr W last updated on 03/Oct/22

{(\cos \frac{π}{2} + i \cos \frac{π}{8})}^{- 5}

= {(0 + \frac{\sqrt{2 + \sqrt{2}}}{2} i)}^{- 5}

= {(\frac{\sqrt{2 + \sqrt{2}}}{2})}^{- 5} {(i)}^{- 5}

= \frac{2^{5}}{{(\sqrt{2 + \sqrt{2}})}^{5}} \times \frac{i}{i^{6}}

= \frac{32}{{(\sqrt{2 + \sqrt{2}})}^{5}} \times \frac{i}{{(- 1)}^{3}}

= - \frac{32 i}{{(\sqrt{2 + \sqrt{2}})}^{5}}

Answered by ranjankumar last updated on 03/Oct/22