c-2-x-2-1-c-x-how-many-complex-roots-

Question Number 38907 by ajfour last updated on 01/Jul/18

\sqrt{c^{2} + x^{2}} = 1 + \frac{c}{x}

h o w m a n y c o m p l e x r o o t s ?

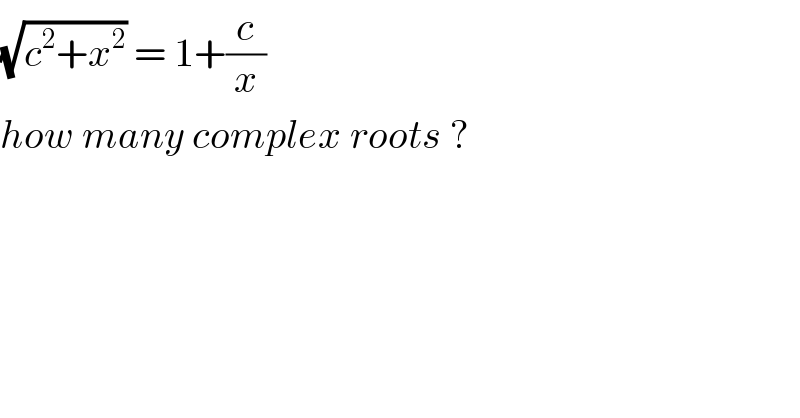
Commented by ajfour last updated on 01/Jul/18

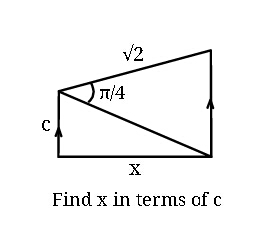
Commented by MJS last updated on 01/Jul/18

\sqrt{c^{2} + x^{2}} = \frac{c + x}{x} has only 3 roots . if you square

to solve it, you get 4 roots of which one is no

solution of the original equation

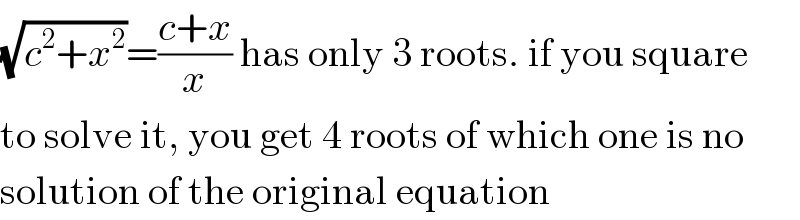
Commented by MrW3 last updated on 01/Jul/18

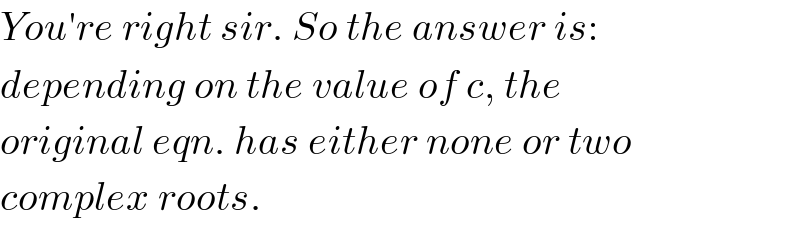
{Y o u}^{'} r e r i g h t s i r . S o t h e a n s w e r i s :

d e p e n d i n g o n t h e v a l u e o f c, t h e

o r i g i n a l e q n . h a s e i t h e r n o n e o r t w o

c o m p l e x r o o t s .

Commented by ajfour last updated on 01/Jul/18

T h a n k s f o r t h e t r u t h, s i r .

Commented by MJS last updated on 01/Jul/18

we can find the value of c = c with

c = c \Rightarrow f (x) = \sqrt{x^{2} + c^{2}} - \frac{x + c}{x} = 0 has exactly 2 real solutions

c < c \Rightarrow f (x) = 0 has 3 real solutions

c > c \Rightarrow f (x) = 0 has 1 real and 2 complex solutions

x^{4} + (c^{2} - 1) x^{2} - 2 c x - c^{2} = 0

{(x - α)}^{2} (x + α - β) (x + α + β) = 0

{it}^{'} s the same way as several times before, in

this special case we get 3 equations in α, β, c

with α > 0, β > 0, c < 0 and β^{2} is the only real

solution of a polynome of 3^{rd} degree .

x = - α + β should be the “ {wrong}^{″} solution I guess

I might post it later but it should be easy to

solve

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18

c^{2} + x^{2} = 1 + \frac{2 c}{x} + \frac{c^{2}}{x^{2}}

c^{2} + x^{2} = \frac{x^{2} + 2 c x + c^{2}}{x^{2}}

x^{2} c^{2} + x^{4} = x^{2} + 2 c x + c^{2}

x^{4} + x^{2} (c^{2} - 1) - 2 c x - c^{2} = 0

f (x) = x^{4} + 0 . x^{3} + (c^{2} - 1) x^{2} - 2 c x - c^{2}

l e t c^{2} > 1 u s i n g D e s c a r t s r u l e o f s i g n

o n e s i g n c h a n g e s o o n e p o s i t i v e r o o t

f (- x) = x^{4} + 0 . (- x^{3}) + (c^{2} - 1) x^{2} + 2 c x - c^{2}

o n e s i g n c h a n g e s o o n e n e g d t i v e r o o t

s o 4 - 1 - 1 = 2 c o m p l x r o o t

n o w i f c^{2} < 1

f (x) = x^{4} + 0 . x^{3} - (1 - c^{2}) x^{2} + 2 c x - c^{2}

2 + v e r o o t

f (- x) = x^{4} - (1 - c^{2}) x^{2} - 2 c x - c^{2}

1 (- v e) r o o t

s o o n e c o m p l e x r o o t

Commented by ajfour last updated on 01/Jul/18

T h a n k y o u v e r y m u c h, S i r T a n m a y .

Facebook Tweet Pin