Question Number 120195 by SOMEDAVONG last updated on 30/Oct/20
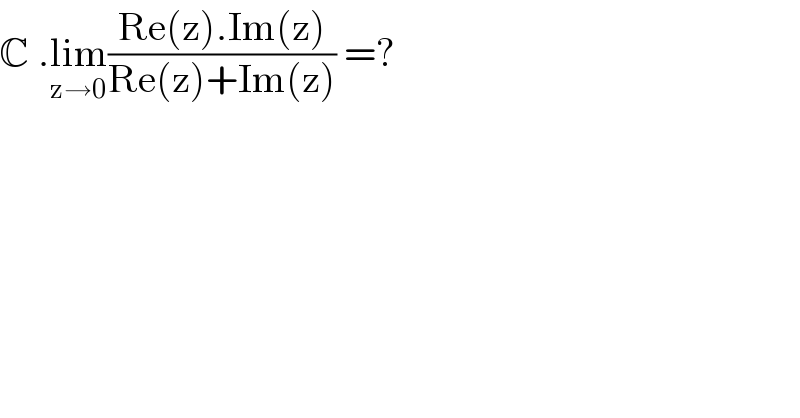
$$\mathbb{C}\:.\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{Re}\left(\mathrm{z}\right).\mathrm{Im}\left(\mathrm{z}\right)}{\mathrm{Re}\left(\mathrm{z}\right)+\mathrm{Im}\left(\mathrm{z}\right)}\:=? \\ $$
Answered by snipers237 last updated on 30/Oct/20
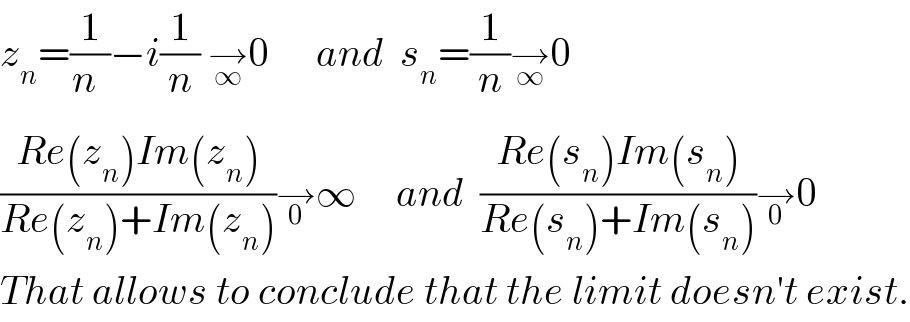
$${z}_{{n}} =\frac{\mathrm{1}}{{n}_{} }−{i}\frac{\mathrm{1}}{{n}}\:\underset{\infty} {\rightarrow}\mathrm{0}\:\:\:\:\:\:{and}\:\:{s}_{{n}} =\frac{\mathrm{1}}{{n}}\underset{\infty} {\rightarrow}\mathrm{0} \\ $$$$\frac{{Re}\left({z}_{{n}} \right){Im}\left({z}_{{n}} \right)}{{Re}\left({z}_{{n}} \right)+{Im}\left({z}_{{n}} \right)}\underset{\mathrm{0}} {\rightarrow}\infty\:\:\:\:\:{and}\:\:\frac{{Re}\left({s}_{{n}} \right){Im}\left({s}_{{n}} \right)}{{Re}\left({s}_{{n}} \right)+{Im}\left({s}_{{n}} \right)}\underset{\mathrm{0}} {\rightarrow}\mathrm{0} \\ $$$${That}\:{allows}\:{to}\:{conclude}\:{that}\:{the}\:{limit}\:{doesn}'{t}\:{exist}. \\ $$
Commented by SOMEDAVONG last updated on 30/Oct/20

$$\mathrm{Thanks}\:\mathrm{sir}\: \\ $$
Answered by MJS_new last updated on 30/Oct/20
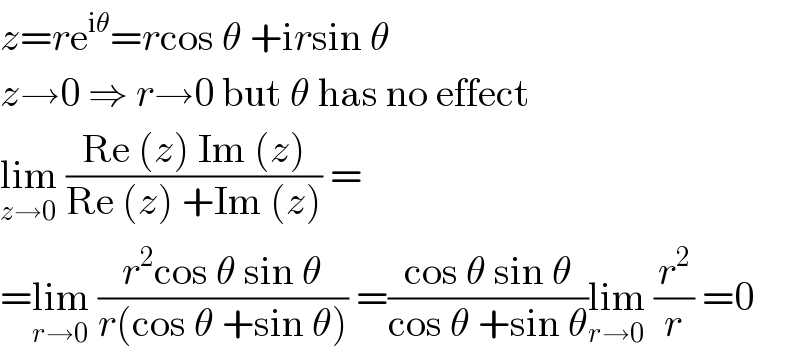
$${z}={r}\mathrm{e}^{\mathrm{i}\theta} ={r}\mathrm{cos}\:\theta\:+\mathrm{i}{r}\mathrm{sin}\:\theta \\ $$$${z}\rightarrow\mathrm{0}\:\Rightarrow\:{r}\rightarrow\mathrm{0}\:\mathrm{but}\:\theta\:\mathrm{has}\:\mathrm{no}\:\mathrm{effect} \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{Re}\:\left({z}\right)\:\mathrm{Im}\:\left({z}\right)}{\mathrm{Re}\:\left({z}\right)\:+\mathrm{Im}\:\left({z}\right)}\:= \\ $$$$=\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{r}^{\mathrm{2}} \mathrm{cos}\:\theta\:\mathrm{sin}\:\theta}{{r}\left(\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta\right)}\:=\frac{\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta}\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{r}^{\mathrm{2}} }{{r}}\:=\mathrm{0}\: \\ $$
Answered by MJS_new last updated on 30/Oct/20
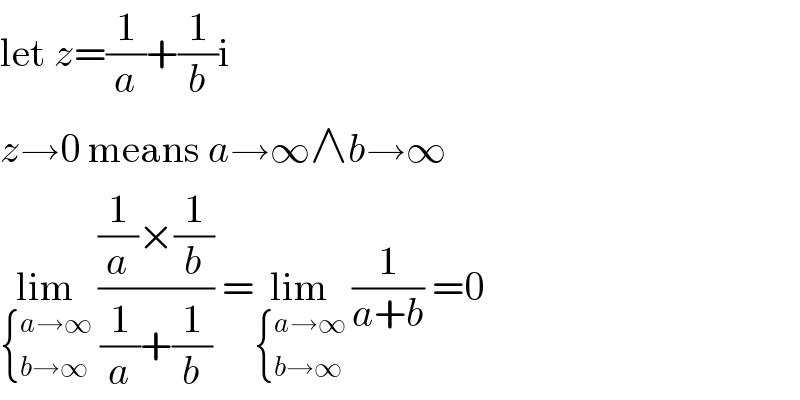
$$\mathrm{let}\:{z}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\mathrm{i} \\ $$$${z}\rightarrow\mathrm{0}\:\mathrm{means}\:{a}\rightarrow\infty\wedge{b}\rightarrow\infty \\ $$$$\underset{\begin{cases}{{a}\rightarrow\infty}\\{{b}\rightarrow\infty}\end{cases}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{{a}}×\frac{\mathrm{1}}{{b}}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}}\:=\underset{\begin{cases}{{a}\rightarrow\infty}\\{{b}\rightarrow\infty}\end{cases}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{a}+{b}}\:=\mathrm{0} \\ $$
