Question Number 185169 by a.lgnaoui last updated on 18/Jan/23

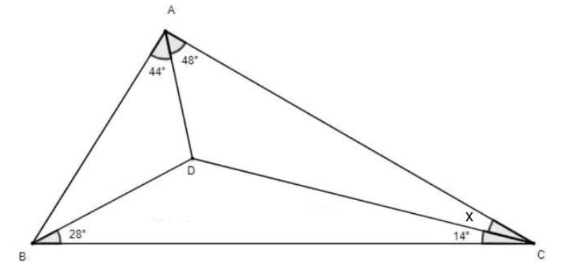
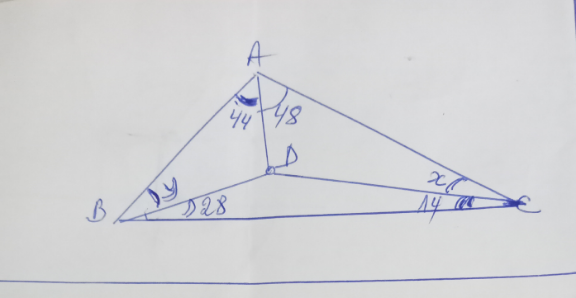
$${calcul}\:{de}\:{l}'\:{angle}\:\boldsymbol{{x}} \\ $$$$\bigtriangleup{ABD}\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{y}}{\mathrm{AD}}=\frac{\mathrm{sin44}\:}{\mathrm{BD}}\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{ADC}\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{AD}}=\frac{\mathrm{sin48}\:}{\mathrm{DC}}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\mathrm{BD}\:\mathrm{sin}\:\mathrm{y}=\mathrm{ADsin}\:\mathrm{44} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\mathrm{DCsinx}\:=\mathrm{ADsin}\:\mathrm{48} \\ $$$$ \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\Leftrightarrow\:\frac{\mathrm{BDsin}\:\mathrm{y}}{\mathrm{DCsin}\:\mathrm{x}}=\frac{\mathrm{sin}\:\mathrm{44}}{\mathrm{sin}\:\mathrm{48}}\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\bigtriangleup{BDC}\:\:\:\:\frac{\mathrm{sin}\:\mathrm{14}}{\mathrm{BD}}=\frac{\mathrm{sin}\:\mathrm{28}}{\mathrm{DC}} \\ $$$$\:\:\:\:\:\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{sin}\:\mathrm{14}}{\mathrm{sin}\:\mathrm{28}} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\frac{\mathrm{sin}\:\mathrm{14}×}{\mathrm{sin}\:\mathrm{28}×}\frac{\mathrm{sin}\:\mathrm{y}}{\mathrm{sin}\:\mathrm{x}}=\frac{\mathrm{sin}\:\mathrm{44}}{\mathrm{sin}\:\mathrm{48}}\: \\ $$$${Relation}\:{entre}\:\boldsymbol{{x}}\:{et}\:\:\boldsymbol{{y}} \\ $$$$\bigtriangleup{ABC}\:\:\:\:\left(\measuredangle{A}\:\:+\measuredangle{B}+\:\:\measuredangle{C}\right)=\mathrm{180} \\ $$$$\:\mathrm{48}+\mathrm{44}+{y}+\mathrm{28}+\mathrm{14}+{x}=\mathrm{180} \\ $$$${x}+{y}=\mathrm{46}\:\Rightarrow\:\:\:\:{y}=\mathrm{46}−{x} \\ $$$$\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{y}}=\frac{\mathrm{sin}\:\mathrm{48}×\mathrm{sin}\:\mathrm{28}}{\mathrm{sin}\:\mathrm{44}×\mathrm{sin}\:\mathrm{14}} \\ $$$$\frac{\mathrm{sinx}}{\mathrm{sin}\left(\mathrm{46}−\mathrm{x}\right)}=\frac{\mathrm{2sin}\:\mathrm{48}×\mathrm{cos}\:\mathrm{14}}{\mathrm{sin}\:\mathrm{44}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{46cos}\:\mathrm{x}−\mathrm{cos}\:\mathrm{46sin}\:\mathrm{x}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}\left(\mathrm{sin}\:\mathrm{46}−\mathrm{tan}\:\mathrm{x}×\mathrm{cos}\:\mathrm{46}\right)} \\ $$$$=\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{46}−\mathrm{cos}\:\mathrm{46}×\mathrm{tan}\:\mathrm{x}} \\ $$$$\mathrm{sin}\:\mathrm{44}×\mathrm{tan}\:\mathrm{x}=\mathrm{2sin}\:\mathrm{48}×\mathrm{cos}\:\mathrm{14}\left(\mathrm{sin}\:\mathrm{46}−\mathrm{cos}\:\mathrm{46tan}\:\mathrm{x}\right) \\ $$$$\left(\mathrm{sin}\:\mathrm{44}+\mathrm{2sin}\:\mathrm{48cos}\:\mathrm{14}×\mathrm{cos}\:\mathrm{46}\right)\mathrm{tan}\:\mathrm{x}= \\ $$$$\mathrm{2sin}\:\mathrm{48cos}\:\mathrm{14}×\mathrm{sin}\:\mathrm{46} \\ $$$$ \\ $$$$\:\:\mathrm{tan}\:\mathrm{x}=\frac{\mathrm{2sin}\:\mathrm{48}×\mathrm{cos}\:\mathrm{14}×\mathrm{sin}\:\:\mathrm{46}}{\mathrm{sin}\:\mathrm{44}+\mathrm{2sin}\:\mathrm{48}×\mathrm{cos}\:\mathrm{14}×\mathrm{cos}\:\mathrm{46}} \\ $$$$\mathrm{sin}\:\mathrm{44}=\:\:\:\mathrm{sin}\:\mathrm{48}=\:\:\:\mathrm{sin}\:\mathrm{46} \\ $$$$\mathrm{cos}\:\mathrm{14}=\:\:\:\:\mathrm{cos}\:\mathrm{46}=\:\:\:\:\: \\ $$$$\mathrm{tan}\:\boldsymbol{\mathrm{x}}=\mathrm{0},\mathrm{61150462} \\ $$$$ \\ $$$${soit}:\:\:\:\:\:\boldsymbol{\mathrm{X}}=\mathrm{31},\mathrm{446}^{°} \:\: \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 18/Jan/23
Answered by a.lgnaoui last updated on 18/Jan/23
Commented by a.lgnaoui last updated on 18/Jan/23
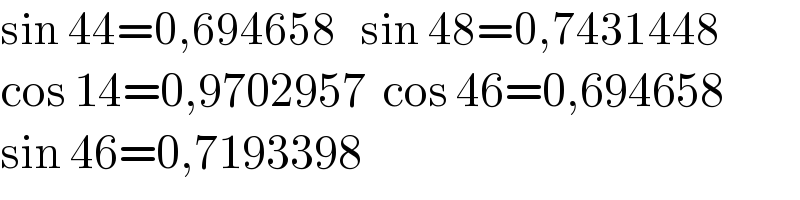
$$\mathrm{sin}\:\mathrm{44}=\mathrm{0},\mathrm{694658}\:\:\:\mathrm{sin}\:\mathrm{48}=\mathrm{0},\mathrm{7431448} \\ $$$$\mathrm{cos}\:\mathrm{14}=\mathrm{0},\mathrm{9702957}\:\:\mathrm{cos}\:\mathrm{46}=\mathrm{0},\mathrm{694658} \\ $$$$\mathrm{sin}\:\mathrm{46}=\mathrm{0},\mathrm{7193398} \\ $$
Commented by a.lgnaoui last updated on 18/Jan/23

$${Recapitulation} \\ $$$$−−−−−−−−−−− \\ $$$$\measuredangle{ACD}={x}=\mathrm{31},\mathrm{446} \\ $$$$\measuredangle{CDA}=\mathrm{100},\mathrm{55} \\ $$$$\measuredangle{ADB}=\mathrm{121},\mathrm{45} \\ $$$$\measuredangle{ABD}={y}=\mathrm{14},\mathrm{55} \\ $$$$\measuredangle{BDC}=\mathrm{138} \\ $$$$ \\ $$
