Question Number 181360 by lapache last updated on 24/Nov/22
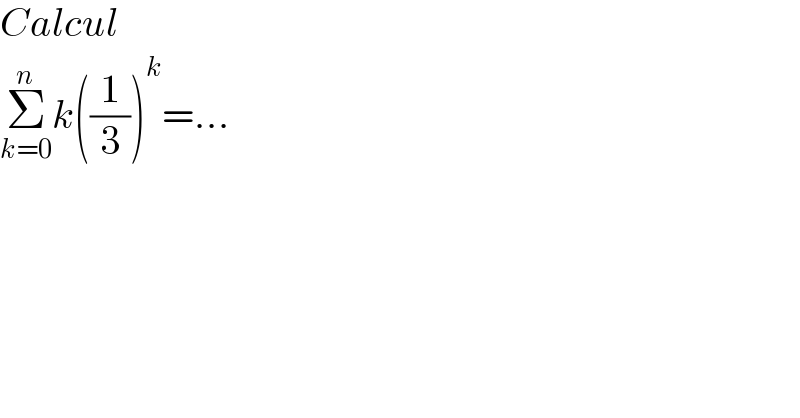
$${Calcul} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{k}} =… \\ $$
Answered by mahdipoor last updated on 24/Nov/22
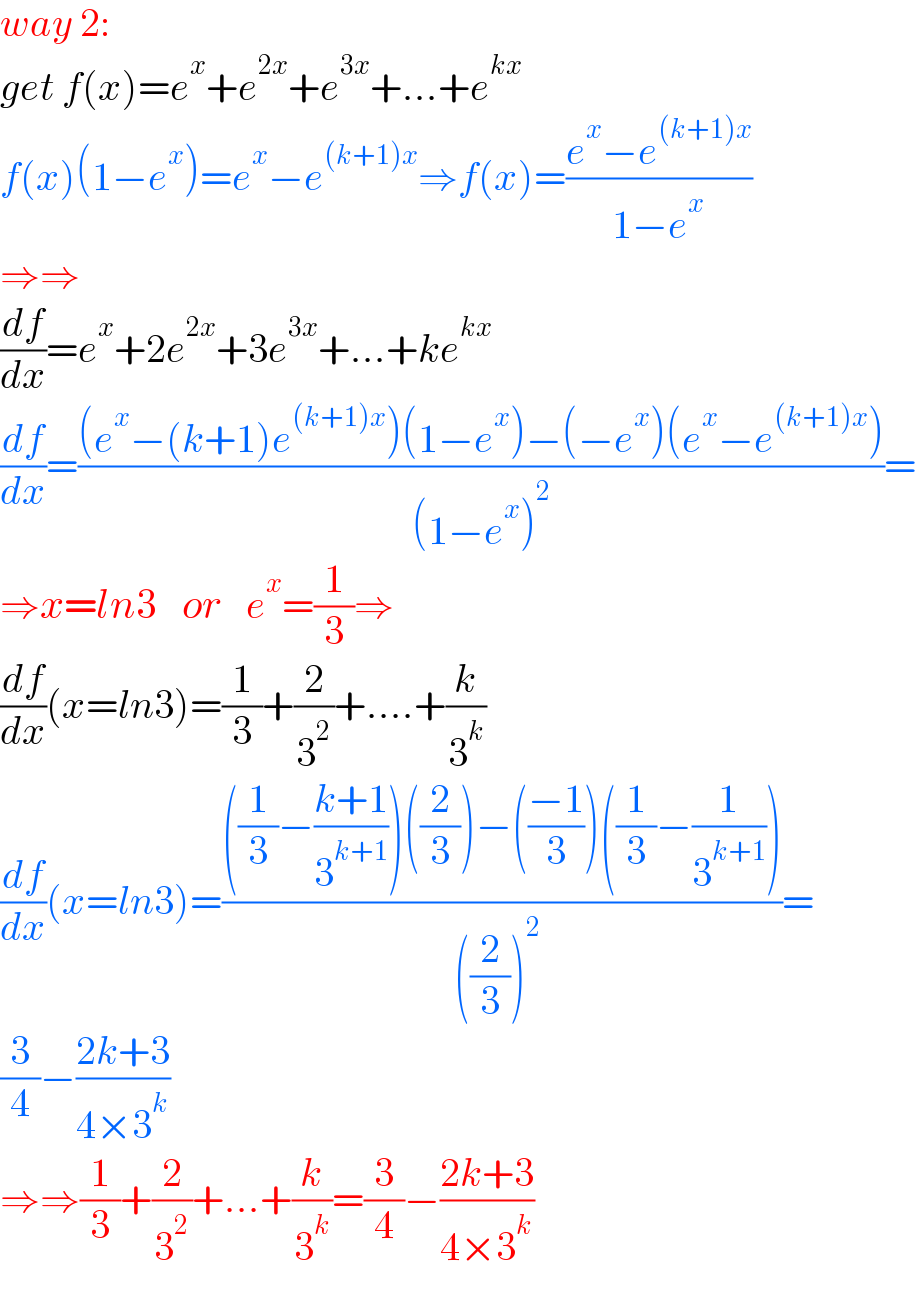
$${way}\:\mathrm{2}: \\ $$$${get}\:{f}\left({x}\right)={e}^{{x}} +{e}^{\mathrm{2}{x}} +{e}^{\mathrm{3}{x}} +…+{e}^{{kx}} \\ $$$${f}\left({x}\right)\left(\mathrm{1}−{e}^{{x}} \right)={e}^{{x}} −{e}^{\left({k}+\mathrm{1}\right){x}} \Rightarrow{f}\left({x}\right)=\frac{{e}^{{x}} −{e}^{\left({k}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{x}} } \\ $$$$\Rightarrow\Rightarrow \\ $$$$\frac{{df}}{{dx}}={e}^{{x}} +\mathrm{2}{e}^{\mathrm{2}{x}} +\mathrm{3}{e}^{\mathrm{3}{x}} +…+{ke}^{{kx}} \\ $$$$\frac{{df}}{{dx}}=\frac{\left({e}^{{x}} −\left({k}+\mathrm{1}\right){e}^{\left({k}+\mathrm{1}\right){x}} \right)\left(\mathrm{1}−{e}^{{x}} \right)−\left(−{e}^{{x}} \right)\left({e}^{{x}} −{e}^{\left({k}+\mathrm{1}\right){x}} \right)}{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} }= \\ $$$$\Rightarrow{x}={ln}\mathrm{3}\:\:\:{or}\:\:\:{e}^{{x}} =\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow \\ $$$$\frac{{df}}{{dx}}\left({x}={ln}\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+….+\frac{{k}}{\mathrm{3}^{{k}} } \\ $$$$\frac{{df}}{{dx}}\left({x}={ln}\mathrm{3}\right)=\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{{k}+\mathrm{1}}{\mathrm{3}^{{k}+\mathrm{1}} }\right)\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\left(\frac{−\mathrm{1}}{\mathrm{3}}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}^{{k}+\mathrm{1}} }\right)}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}\:\:} }= \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{2}{k}+\mathrm{3}}{\mathrm{4}×\mathrm{3}^{{k}} } \\ $$$$\Rightarrow\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{{k}}{\mathrm{3}^{{k}} }=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{2}{k}+\mathrm{3}}{\mathrm{4}×\mathrm{3}^{{k}} } \\ $$
Answered by SEKRET last updated on 24/Nov/22
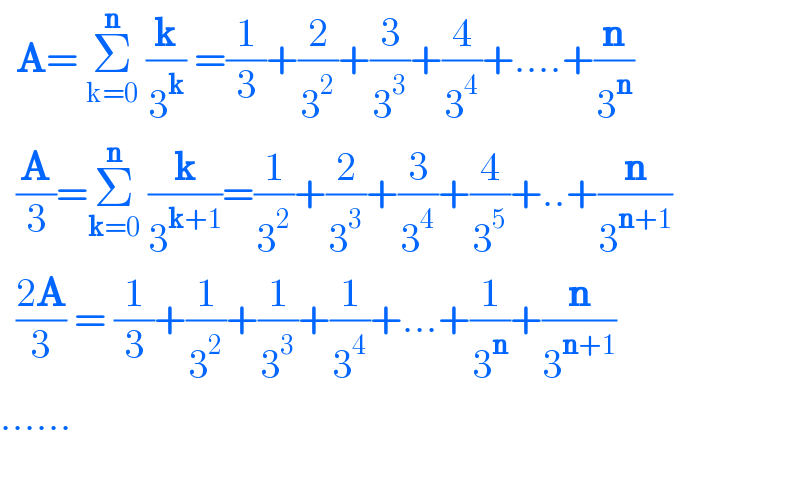
$$\:\:\boldsymbol{\mathrm{A}}=\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\:\frac{\boldsymbol{\mathrm{k}}}{\mathrm{3}^{\boldsymbol{\mathrm{k}}} }\:=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{4}} }+….+\frac{\boldsymbol{\mathrm{n}}}{\mathrm{3}^{\boldsymbol{\mathrm{n}}} } \\ $$$$\:\:\frac{\boldsymbol{\mathrm{A}}}{\mathrm{3}}=\underset{\boldsymbol{\mathrm{k}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\:\frac{\boldsymbol{\mathrm{k}}}{\mathrm{3}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{3}^{\mathrm{4}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{5}} }+..+\frac{\boldsymbol{\mathrm{n}}}{\mathrm{3}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} } \\ $$$$\:\:\frac{\mathrm{2}\boldsymbol{\mathrm{A}}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{\boldsymbol{\mathrm{n}}} }+\frac{\boldsymbol{\mathrm{n}}}{\mathrm{3}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} } \\ $$$$…… \\ $$$$ \\ $$
Answered by mahdipoor last updated on 24/Nov/22
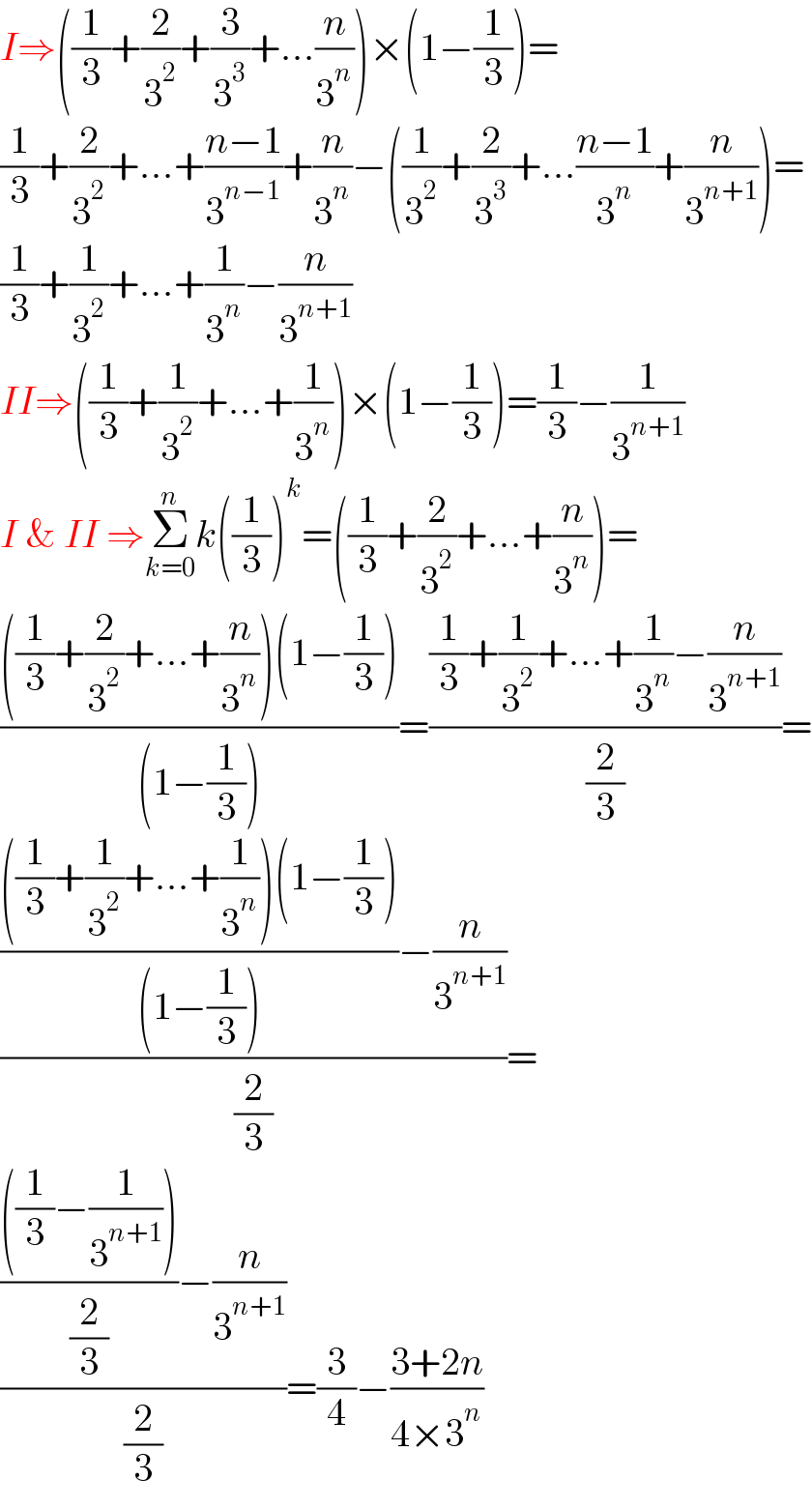
$${I}\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{3}^{\mathrm{3}} }+…\frac{{n}}{\mathrm{3}^{{n}} }\right)×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{{n}−\mathrm{1}}{\mathrm{3}^{{n}−\mathrm{1}} }+\frac{{n}}{\mathrm{3}^{{n}} }−\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{3}} }+…\frac{{n}−\mathrm{1}}{\mathrm{3}^{{n}} }+\frac{{n}}{\mathrm{3}^{{n}+\mathrm{1}} }\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{{n}} }−\frac{{n}}{\mathrm{3}^{{n}+\mathrm{1}} } \\ $$$${II}\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{{n}} }\right)×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}^{{n}+\mathrm{1}} } \\ $$$${I}\:\&\:{II}\:\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{k}} =\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{{n}}{\mathrm{3}^{{n}} }\right)= \\ $$$$\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{{n}}{\mathrm{3}^{{n}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{{n}} }−\frac{{n}}{\mathrm{3}^{{n}+\mathrm{1}} }}{\frac{\mathrm{2}}{\mathrm{3}}}= \\ $$$$\frac{\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{3}^{{n}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}−\frac{{n}}{\mathrm{3}^{{n}+\mathrm{1}} }}{\frac{\mathrm{2}}{\mathrm{3}}}= \\ $$$$\frac{\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}^{{n}+\mathrm{1}} }\right)}{\frac{\mathrm{2}}{\mathrm{3}}}−\frac{{n}}{\mathrm{3}^{{n}+\mathrm{1}} }}{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{3}+\mathrm{2}{n}}{\mathrm{4}×\mathrm{3}^{{n}} } \\ $$
