Question Number 165493 by SANOGO last updated on 02/Feb/22
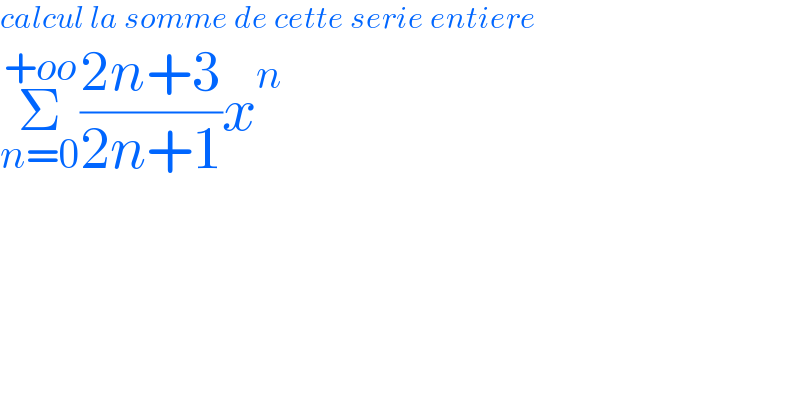
$${calcul}\:{la}\:{somme}\:{de}\:{cette}\:{serie}\:{entiere} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{+{oo}} {\sum}}\frac{\mathrm{2}{n}+\mathrm{3}}{\mathrm{2}{n}+\mathrm{1}}{x}^{{n}} \\ $$
Answered by TheSupreme last updated on 02/Feb/22

$${S}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\right){x}^{{n}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−{x}}+\Sigma\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}{x}^{{n}} \\ $$$${x}={s}^{\mathrm{2}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }+\frac{\mathrm{2}}{{s}}\Sigma\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{s}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Sigma\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{s}^{\mathrm{2}{n}+\mathrm{1}} =\Sigma\int{s}^{\mathrm{2}{n}} =\int\Sigma{s}^{\mathrm{2}{n}} =\int\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }={arctanh}\left({s}\right) \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}{arctanh}\left(\sqrt{{x}}\right) \\ $$$$\mid{x}\mid<\mathrm{1} \\ $$
Answered by Mathspace last updated on 02/Feb/22
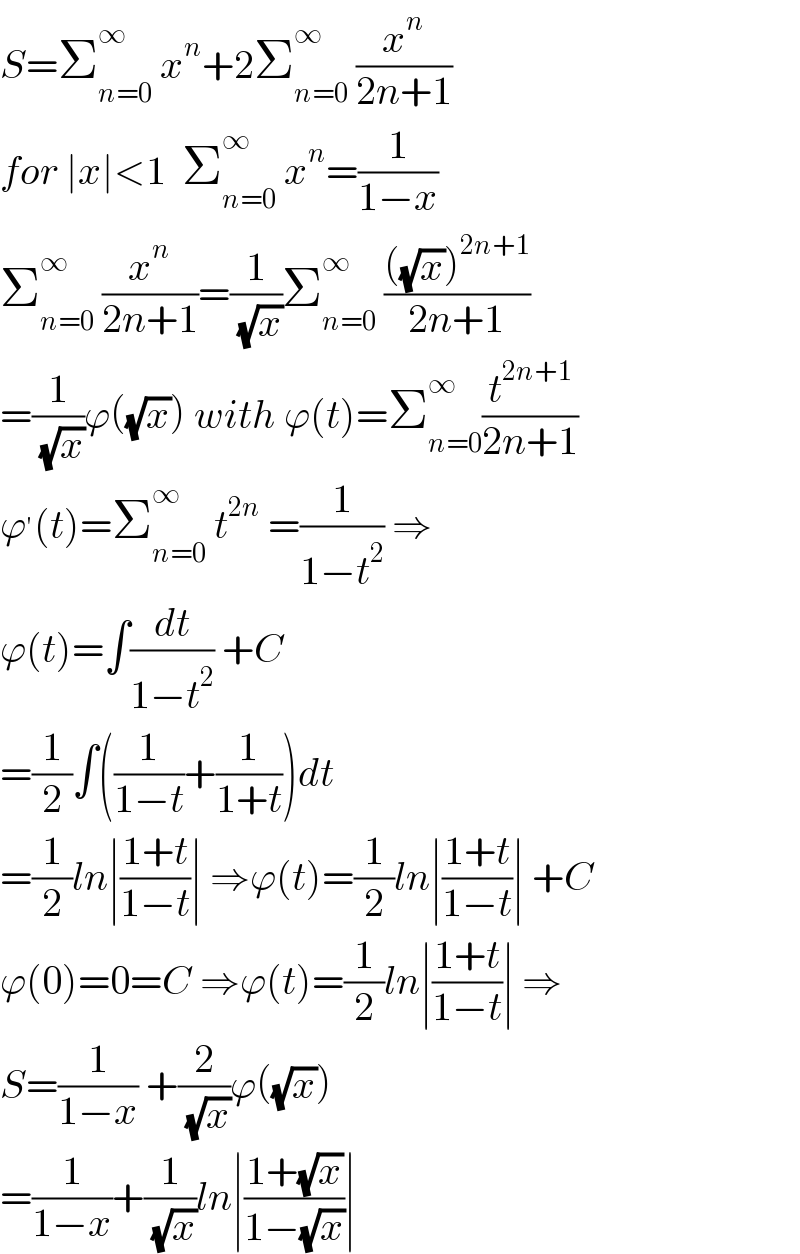
$${S}=\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} +\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$${for}\:\mid{x}\mid<\mathrm{1}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{{x}}}\sum_{{n}=\mathrm{0}} ^{\infty\:} \:\frac{\left(\sqrt{{x}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{x}}}\varphi\left(\sqrt{{x}}\right)\:{with}\:\varphi\left({t}\right)=\sum_{{n}=\mathrm{0}} ^{\infty\:} \frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\varphi^{'} \left({t}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{\mathrm{2}{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\varphi\left({t}\right)=\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\:\Rightarrow\varphi\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\:+{C} \\ $$$$\varphi\left(\mathrm{0}\right)=\mathrm{0}={C}\:\Rightarrow\varphi\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\:\Rightarrow \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:+\frac{\mathrm{2}}{\:\sqrt{{x}}}\varphi\left(\sqrt{{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}{ln}\mid\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\mid \\ $$
