Question Number 172989 by SANOGO last updated on 04/Jul/22
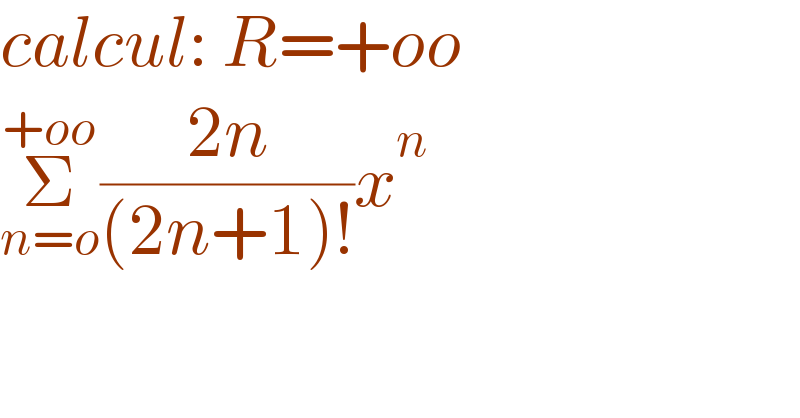
$${calcul}:\:{R}=+{oo}\: \\ $$$$\underset{{n}={o}} {\overset{+{oo}} {\sum}}\frac{\mathrm{2}{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{x}^{{n}} \\ $$
Answered by mr W last updated on 04/Jul/22
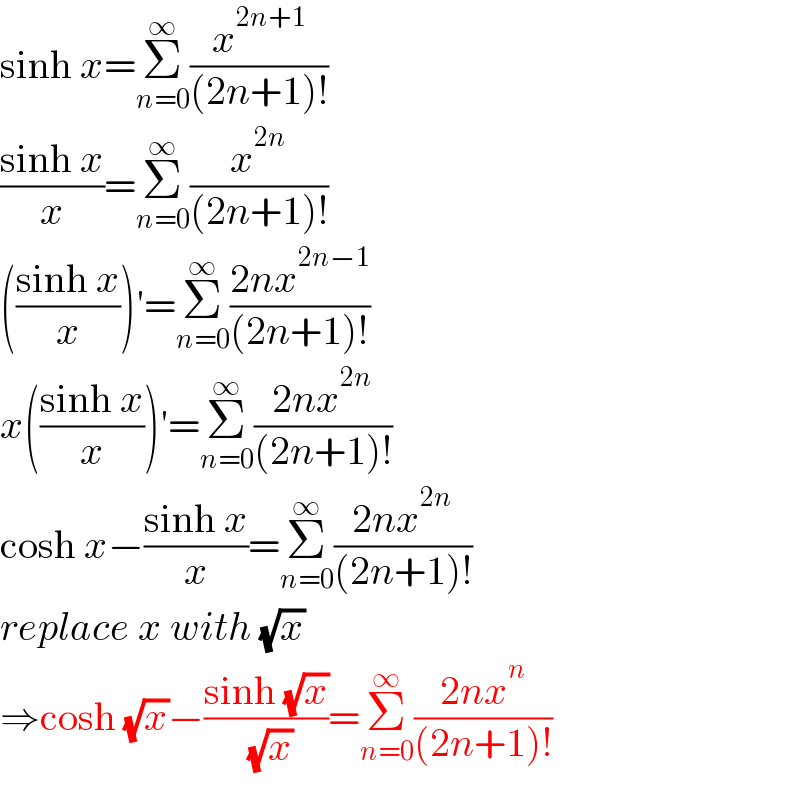
$$\mathrm{sinh}\:{x}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{sinh}\:{x}}{{x}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\left(\frac{\mathrm{sinh}\:{x}}{{x}}\right)'=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{nx}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${x}\left(\frac{\mathrm{sinh}\:{x}}{{x}}\right)'=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{nx}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\mathrm{cosh}\:{x}−\frac{\mathrm{sinh}\:{x}}{{x}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{nx}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${replace}\:{x}\:{with}\:\sqrt{{x}} \\ $$$$\Rightarrow\mathrm{cosh}\:\sqrt{{x}}−\frac{\mathrm{sinh}\:\sqrt{{x}}}{\:\sqrt{{x}}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{nx}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
Commented by Tawa11 last updated on 06/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
