Question Number 149503 by mathdanisur last updated on 05/Aug/21
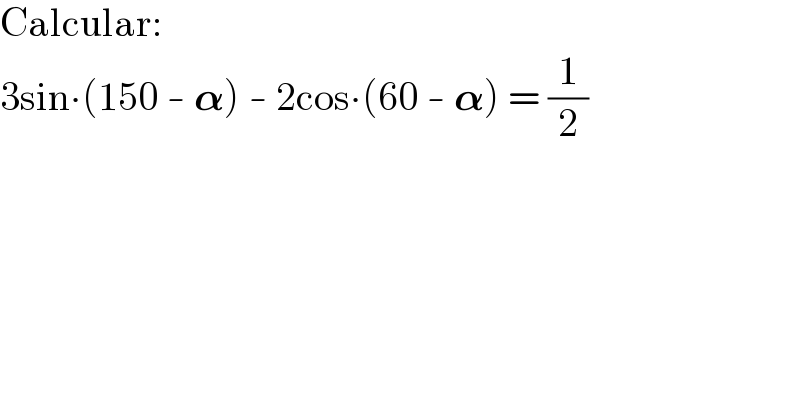
$$\mathrm{Calcular}: \\ $$$$\mathrm{3sin}\centerdot\left(\mathrm{150}\:-\:\boldsymbol{\alpha}\right)\:-\:\mathrm{2cos}\centerdot\left(\mathrm{60}\:-\:\boldsymbol{\alpha}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 05/Aug/21
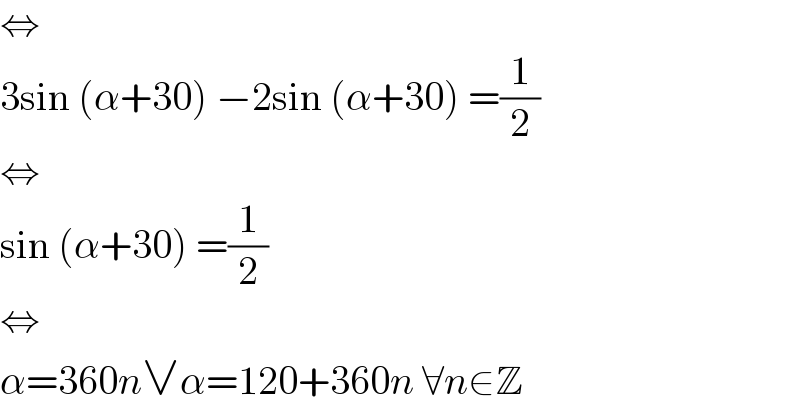
$$\Leftrightarrow \\ $$$$\mathrm{3sin}\:\left(\alpha+\mathrm{30}\right)\:−\mathrm{2sin}\:\left(\alpha+\mathrm{30}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{sin}\:\left(\alpha+\mathrm{30}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Leftrightarrow \\ $$$$\alpha=\mathrm{360}{n}\vee\alpha=\mathrm{120}+\mathrm{360}{n}\:\forall{n}\in\mathbb{Z} \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Cool},\:\mathrm{thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}} \\ $$
Answered by Ar Brandon last updated on 05/Aug/21
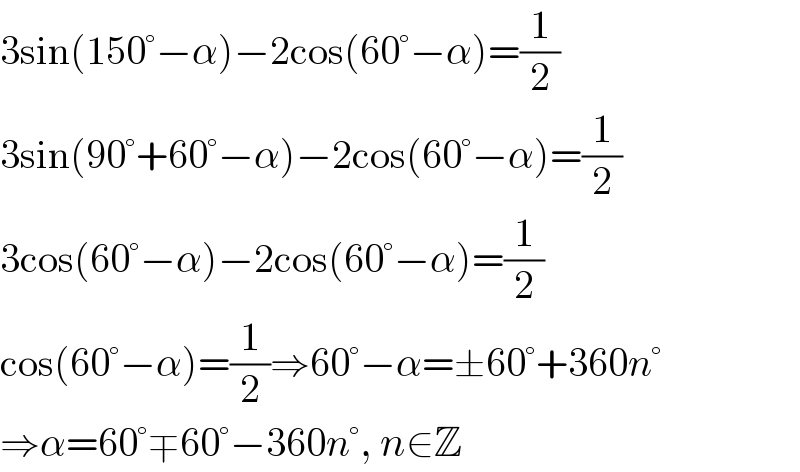
$$\mathrm{3sin}\left(\mathrm{150}°−\alpha\right)−\mathrm{2cos}\left(\mathrm{60}°−\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3sin}\left(\mathrm{90}°+\mathrm{60}°−\alpha\right)−\mathrm{2cos}\left(\mathrm{60}°−\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3cos}\left(\mathrm{60}°−\alpha\right)−\mathrm{2cos}\left(\mathrm{60}°−\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\left(\mathrm{60}°−\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{60}°−\alpha=\pm\mathrm{60}°+\mathrm{360}{n}° \\ $$$$\Rightarrow\alpha=\mathrm{60}°\mp\mathrm{60}°−\mathrm{360}{n}°,\:{n}\in\mathbb{Z} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$
