Question Number 47058 by maxmathsup by imad last updated on 04/Nov/18
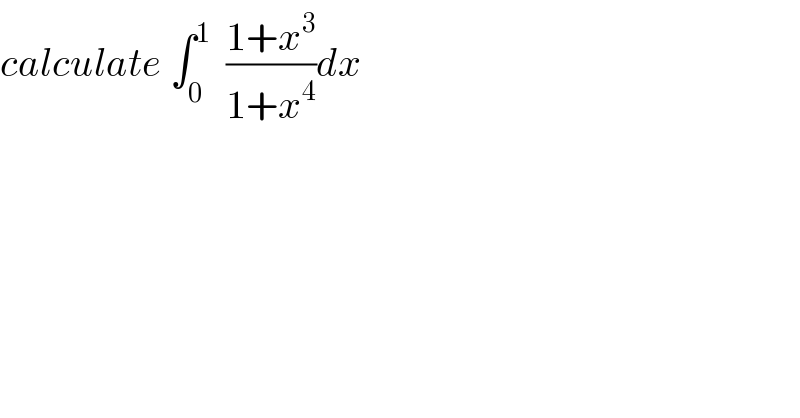
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Nov/18
![∫(dx/(1+x^4 ))+(1/4)∫((4x^3 )/(1+x^4 ))dx I_1 +I_2 I_2 =(1/4)∫((4x^3 )/(1+x^4 ))dx =(1/4)ln(1+x^4 )+c_2 j_2 =∣I_2 ∣_0 ^1 =(1/4)ln(1+1)−(1/4)ln(1+0)→(1/4)ln2 I_1 =(1/2)∫((2/x^2 )/((1/x^2 )+x^2 ))dx =(1/2)[∫(((1+(1/x^2 ))−(1−(1/x^2 )))/(x^2 +(1/x^2 )))dx =(1/2)[∫((d(x−(1/x)))/((x−(1/x))^2 +2))−∫((d(x+(1/x)))/((x+(1/x))^2 −2))] =(1/2)[(1/( (√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/(2(√2)))ln∣(((x+(1/x)−(√2))/(x+(1/x)+(√2))))∣]+c_1 =(1/2)[(1/( (√2)))tan^(−1) (((x^2 −1)/(x(√2))))−(1/(2(√2)))ln∣(((x^2 +1−x(√2))/(x^2 +1+x(√2) )))∣ j_1 =∣I_1 ∣_0 ^1 j_1 =(1/2)[{(1/( (√2)))tan^(−1) (((1−1)/(1×(√2))))−(1/( (√2)))tan^(−1) (((0−1)/(0×(√2))))}− (1/(2(√2)))ln∣(((1+1−(√2))/(1+1+(√2))))∣−(1/(2(√2)))ln∣((1/1))] =(1/2)[{(1/( (√2)))×0−(1/( (√2)))(−(π/2))}−(1/(2(√2)))ln(((2−(√2))/(2+(√2))))] =(π/(4(√2)))−(1/(2(√2)))ln(((2−(√2))/(2+(√2)))) now put limit...](https://www.tinkutara.com/question/Q47069.png)
$$\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{x}^{\mathrm{4}} \right)+{c}_{\mathrm{2}} \\ $$$${j}_{\mathrm{2}} =\mid{I}_{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+\mathrm{0}\right)\rightarrow\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{2} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\right)\mid\right]+{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}−{x}\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} +\mathrm{1}+{x}\sqrt{\mathrm{2}}\:}\right)\mid\right. \\ $$$${j}_{\mathrm{1}} =\mid{I}_{\mathrm{1}} \mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${j}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{1}}{\mathrm{1}×\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{0}−\mathrm{1}}{\mathrm{0}×\sqrt{\mathrm{2}}}\right)\right\}−\right. \\ $$$$\left.\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\left(\frac{\mathrm{1}+\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{1}+\mathrm{1}+\sqrt{\mathrm{2}}}\right)\mid−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\left(\frac{\mathrm{1}}{\mathrm{1}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\mathrm{0}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(−\frac{\pi}{\mathrm{2}}\right)\right\}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\right] \\ $$$$=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\: \\ $$$${now}\:{put}\:{limit}… \\ $$
