Question Number 51987 by maxmathsup by imad last updated on 01/Jan/19
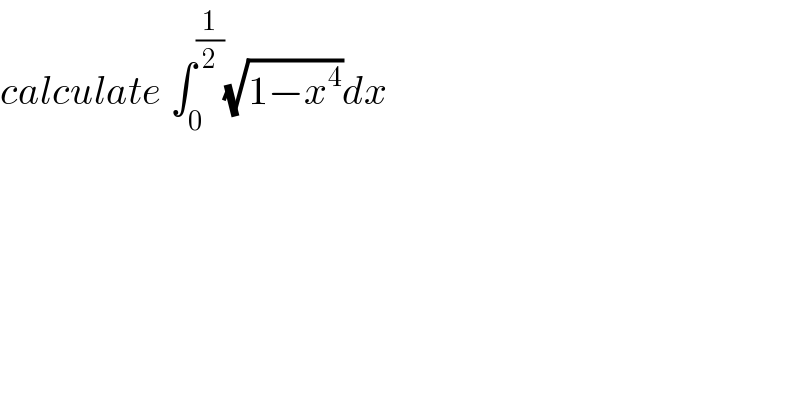
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$
Commented by Abdo msup. last updated on 02/Jan/19
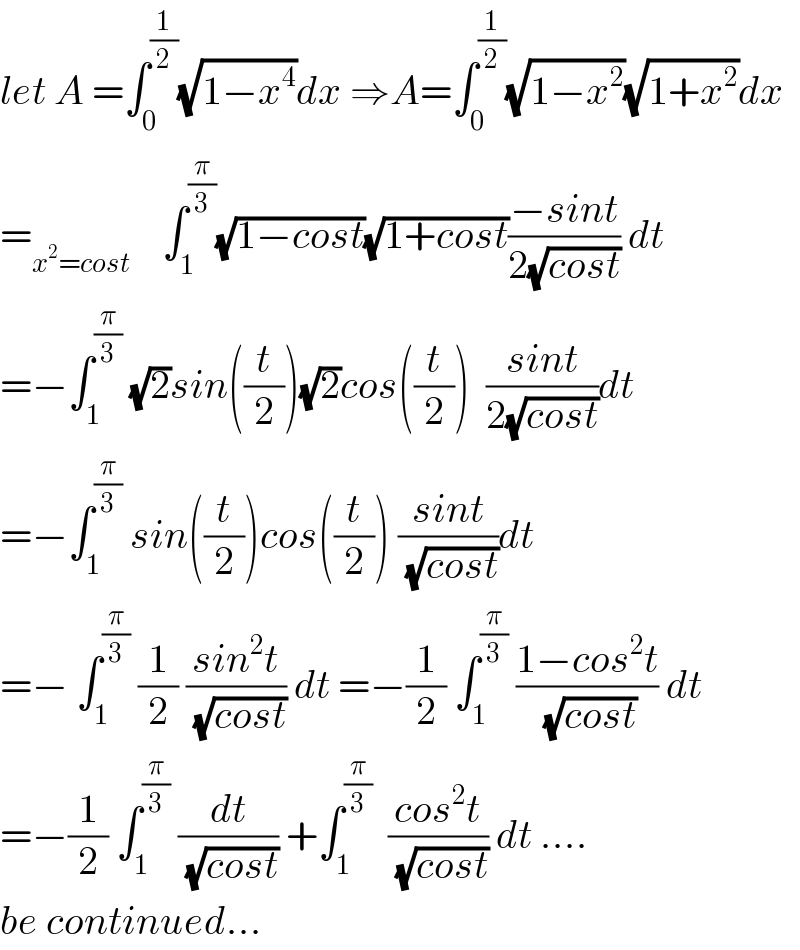
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx}\:\Rightarrow{A}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=_{{x}^{\mathrm{2}} ={cost}} \:\:\:\:\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{\mathrm{1}−{cost}}\sqrt{\mathrm{1}+{cost}}\frac{−{sint}}{\mathrm{2}\sqrt{{cost}}}\:{dt} \\ $$$$=−\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:\sqrt{\mathrm{2}}{sin}\left(\frac{{t}}{\mathrm{2}}\right)\sqrt{\mathrm{2}}{cos}\left(\frac{{t}}{\mathrm{2}}\right)\:\:\frac{{sint}}{\mathrm{2}\sqrt{{cost}}}{dt} \\ $$$$=−\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:{sin}\left(\frac{{t}}{\mathrm{2}}\right){cos}\left(\frac{{t}}{\mathrm{2}}\right)\:\frac{{sint}}{\:\sqrt{{cost}}}{dt} \\ $$$$=−\:\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{sin}^{\mathrm{2}} {t}}{\:\sqrt{{cost}}}\:{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{1}−{cos}^{\mathrm{2}} {t}}{\:\sqrt{{cost}}}\:{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{dt}}{\:\sqrt{{cost}}}\:+\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{{cos}^{\mathrm{2}} {t}}{\:\sqrt{{cost}}}\:{dt}\:…. \\ $$$${be}\:{continued}… \\ $$
Answered by peter frank last updated on 01/Jan/19
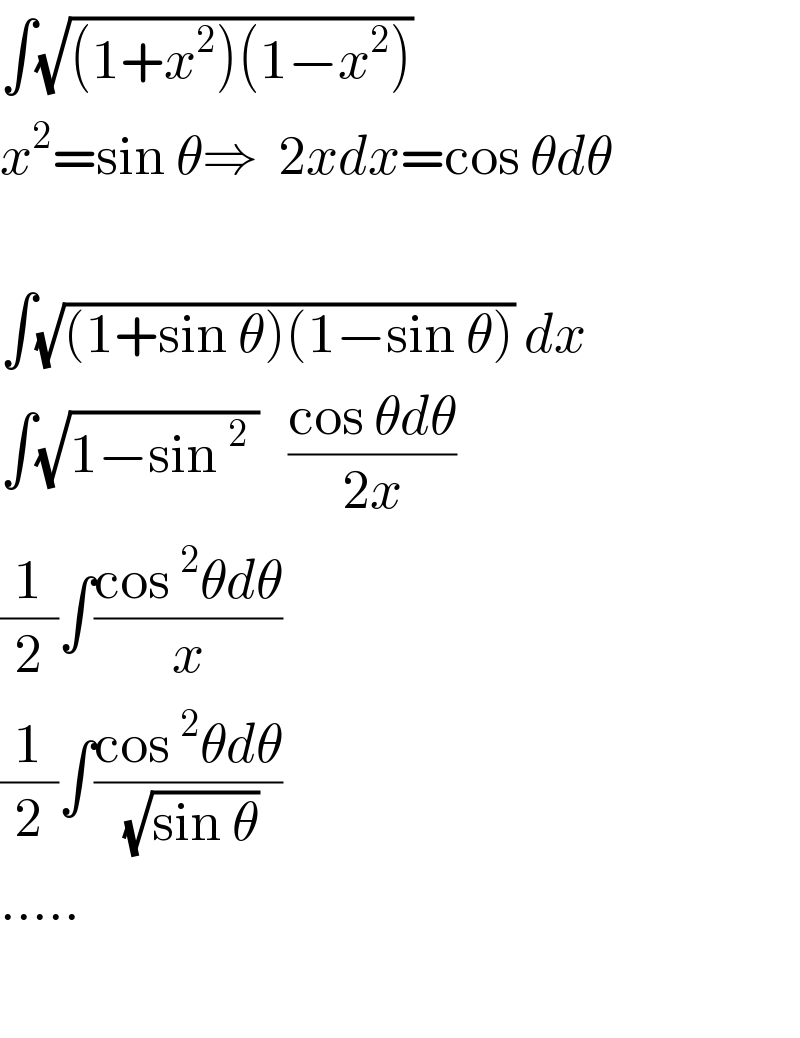
$$\int\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)} \\ $$$${x}^{\mathrm{2}} =\mathrm{sin}\:\theta\Rightarrow\:\:\mathrm{2}{xdx}=\mathrm{cos}\:\theta{d}\theta \\ $$$$ \\ $$$$\int\sqrt{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}\:{dx} \\ $$$$\int\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \:}\:\:\:\frac{\mathrm{cos}\:\theta{d}\theta}{\mathrm{2}{x}}\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}} \\ $$$$….. \\ $$$$ \\ $$
